Костюк - Основы программирования

71

числа без дробной части с округлением). При этом предполагается, что для парамет­ ров графика (вещественных величин dx, dy, a, b, d, ymin и ymax) выполняют­

ся следующие условия:

1)dx и dy имеют целое значение;

2)a и b делятся нацело на dx;

3)d делится нацело на dx;

4)ymin и ymax делятся нацело на dy.

Первое условие может не выполняться, в этом случае необходимо изменить фор­ мат преобразования в процедуре str.

На рис. 3.2 изображен построенный алгоритмами (3.34)–(3.37) график функции f (x) = x3 – 2 x2 – x + 2 при следующих значениях параметров графика: dx=1, dy=4,

a=-2, b=3, d=0.1, ymin=-12 и ymax=8.

8

4

-4

-8

-12

Рис 3.2

Конец примера.

Вопросы и задания

1.Доказать правильность алгоритма (3.2) и вывести формулу его трудоемкости.

72

2.Используя алгоритмы (3.3) и (3.4), написать программу, в которой вводится основание си­ стемы счисления, а затем целое число, записанное в этой системе. После этого вводится основание второй системы счисления, вычисляется и выводится представление числа во второй системе счисления. Придумать принципы представления чисел с основанием, большим, чем 10. Разработать и обосновать тесты для этой программы, протестировать ее и отладить.

3.Доказать правильность алгоритма (3.6), вычисляющего числа Фибоначчи, методом инва­ рианта.

4.Написать и отладить программу, вычисляющую числа Фибоначчи по рекуррентной после­ довательности (3.7) и по урезанной формуле Муавра (3.8) без второго члена. С ее помо­ щью определить, начиная с какого номера по урезанной формуле Муавра можно вычис­ лить числа Фибоначчи с точностью 0.5? С точностью 0.001?

5.Доказать правильность алгоритма (3.8), вычисляющего сумму (3.11) разложения функции sin x, методом инварианта.

6.Объяснить, почему сумму (3.13) нельзя вычислить алгоритмом (3.9). Можно ли придумать другой алгоритм для вычисления этой суммы?

7.Написать и отладить программу, вычисляющую квадратный корень числа по рекуррент­ ной последовательности (3.14) и (для сравнения) с помощью стандартной функции sqrt.

Определить, сколько необходимо вычислить членов последовательности, чтобы добиться относительной точности вычисления квадратного корня 10–6 из чисел 0.0001, 0.01, 0.5, 2, 100, 104, 106.

8.Определить, сколько раз вычисляется функция f (x) в алгоритме (3.11) при заданных входных значениях a, b, eps. Модифицировать алгоритм (3.11) таким образом, чтобы

сэкономить половину вычислений функции.

9. Используя алгоритм (3.11), написать программу, вычисляющую корень функции f (x) = x4 – 10 x3 + 35 x2 – 40 x + 24 на заданном интервале [a, b] с точностью 10–6. С помо­ щью этой программы найти корни функции на интервалах [0.5, 1.5], [1.5, 2.5], [2.5, 3.5], [3.5, 4.5].

10.Используя алгоритм (3.12), написать программу, вычисляющую НОД для двух целых чи­ сел. Разработать и обосновать для нее тесты, провести тестирование и отладку.

11.Довести до конца доказательство алгоритма слияния (3.13) методом инварианта.

12.Провести доказательство правильности алгоритма (3.14) (удаление повторяющихся эле­ ментов из упорядоченного массива) методом инварианта.

13.Провести доказательство правильности алгоритма (3.15) (поиска элемента в неупорядо­ ченном массиве) методом инварианта.

14.Провести полное доказательство правильности алгоритма (3.16) (поиска элемента в упоря­

доченном массиве) методом инварианта. Доказать, что если в массиве имеется несколько элементов, равных p, то алгоритм (3.16) вычислит наименьший номер из них.

15.Провести доказательство правильности алгоритма (3.17) (поиска упорядоченного отрезка максимальной длины в произвольном массиве) методом инварианта.

16.Используя алгоритм (1.8) (простейший алгоритм сортировки), написать алгоритм, выпол­ няющий косвенную упорядоченность массива, и доказать его правильность.

73

17.Написать и отладить программу, которая вводит файл из целых чисел, формирует из них массив и подсчитывает их количество, после чего упорядочивает эти числа по возраста­ нию и записывает в выходной файл.

18.Написать и отладить программу, которая вводит два заранее упорядоченных файла из це­ лых чисел, формирует из них два списка, после чего сливает эти списки в один упорядо­ ченный список и записывает его в выходной файл.

19.Написать и отладить функцию вычисления определенного интеграла произвольной функ­ ции f (x) на интервале [a, b] методом середины прямоугольников. Вычисления выпол­ нять по формуле

пример 3.25).

20.Написать и отладить программу, которая вводит параметры графика dx, dy, a, b, d, ymin, ymax и строит график какой-либо функции (которую можно выбрать произволь­ но) в интервале [a, b].

21.Написать и отладить процедуру построения графика произвольной функции. Процедура должна иметь параметры dx, dy, a, b, d, ymin, ymax (типа real), а также пара­ метр-функцию f (типа func, см. пример 3.25).

22.Написать и отладить программу, которая вводит параметры графика dx, dy, a, b, ymin, ymax, а также n, после чего вводит файл из n значений функции и строит ее график по точкам (в этом случае d=(b-a)/(n-1)).

Глава 4 Рекурсивные алгоритмы

4.1 Что такое рекурсия

Алгоритм можно всегда записать в виде процедуры (или функции), зависящей от входных параметров. Более или менее сложный алгоритм содержит в себе алгоритмы второго уровня, которые внутри него можно записать в виде вызовов процедур. Ал­ горитм можно записать даже так, чтобы он вызывал сам себя! Такой алгоритм назы­ вают рекурсивным. На первый взгляд кажется, что получится порочный круг, и ал­ горитм на компьютере никогда не выполнится до конца. Действительно, при выпол­ нении алгоритм вызывает сам себя, при выполнении этого вызова он снова вызывает сам себя и так далее. Чтобы последовательность вызовов когда-нибудь закончилась, предусматривают, чтобы при каждом вызове хотя бы один входной параметр изме­ нялся. В алгоритме производится проверка этого параметра для того, чтобы при определенном значении повторный вызов не исполнялся. Наиболее просто рекур­ сивный алгоритм записывается по заданной рекуррентной последовательности.

Пример 4.1. Факториал определяется следующей рекуррентной последователь­ ностью ранга 1:

Рекурсивный алгоритм вычисления факториала выглядит весьма лаконично:

function fact(n:integer): integer; begin

if n=0 then fact:=1 (4.1) else fact:=fact(n-1)*n

end;

Конец примера.

Доказательство правильности подобного алгоритма основывается на доказатель­ стве корректности самого определения рекуррентной последовательности. Требуется лишь удостовериться, что при записи алгоритма в него не привнесли ошибок.

Записать рекурсивный алгоритм легко, однако чтобы оценить его эффектив­ ность, необходимо разобраться, как этот алгоритм выполняется исполнителем. Пусть в программе имеется вызов:

75

d:=fact(3);

Вычисления будут следующими:

1)вызывается функция fact, и переменная n заменяется на 3;

2)проверка в операторе if дает ложь, вычисляется оператор в else, в ходе чего вызывается fact(2);

3)проверка в операторе if снова дает ложь, вызывается fact(1);

4)проверка в операторе if еще раз дает ложь, вызывается fact(0);

5) проверка в операторе if дает истина, вычисляется fact:=1;

6)результат подставляется в формулу fact(n-1)*n при n=1, вычисляется fact:=1;

7)результат подставляется в формулу fact(n-1)*n при n=2, вычисляется fact:=2;

8)результат подставляется в формулу fact(n-1)*n при n=3, вычисляется fact:=6;

9)наконец, вычисленное значение fact(3)=6 присваивается переменной d

при первом вызове.

В первых четырех шагах вычисления как бы идут "вглубь", а в следующих четырех – возвращаются "вверх". Для запоминания промежуточных значений в по­ следовательности рекурсивных вызовов исполнителю требуется память, доступ к ко­ торой выполняется по принципу стека. Реализация стека в виде линейного списка рассмотрена в разделе 3.4. Если же стек представить в виде массива, то дополнитель­ но требуется переменная, играющая роль указателя стека. Со стеком можно произво­

дить операции двух видов: запись в стек и извлечение из стека некоторого значения.

При записи в стек следует также выполнять проверку того, что p не превысит размера массива, а при извлечении из стека – что p останется большим нуля.

До начала выполнения алгоритма p=0, т.е. стек считается пустым. При вычис­ лении fact(3) в стеке размещаются те значения n, для которых вызывается fact(n), а также вычисленные значения fact . Заполнение стека и извлечение

значений из него показано в табл. 4.1.

76

В рассмотренном примере за счет рекурсии вычисления в алгоритме имеют цик­ лический характер. Кроме того, для выполнения рекурсивного алгоритма требуется дополнительная память для стека, хотя программист может и не догадываться об этом.

Если память, выделенная для стека, недостаточна, то алгоритм не может быть выполнен до конца: произойдет его аварийное завершение и результат вычислений получен не будет. Поэтому важно уметь оценивать объем памяти, необходимой для рекурсивных вычислений. При каждом рекурсивном вызове требуется разместить в стеке следующую информацию:

1)значения параметров процедуры,

2)возвращаемое значение,

3)внутренние переменные в процедуре (если они есть),

4)адрес возврата – номер команды в программе, которая расположена следом за командой вызова процедуры, и куда происходит возврат после выполнения проце­ дуры.

Число таких размещений равно глубине рекурсии – максимальному количеству последовательных до выхода из рекурсии. Общий объем памяти равен произведению глубины рекурсии на объем памяти, необходимой для выполнения одного вызова

процедуры. Так, например, для рассмотренного алгоритма глубина рекурсии равна n+1, поэтому требуемый объем памяти в несколько раз больше, чем память для це­

лочисленного массива длиной n+1. Особенно много памяти потребуется, если вну­ три рекурсивной процедуры определен массив большого размера.

Что касается времени выполнения рекурсивного алгоритма, то во многих случаях оно пропорционально количеству рекурсивных вызовов. Например, для алгоритма вычисления факториала время пропорционально n+1. Если сравнить его со време­

нем выполнения нерекурсивного (циклического) алгоритма вычисления факториала, то фактически время работы рекурсивного алгоритма окажется в 2–3 раза больше, так как каждое повторение цикла требует от исполнителя меньше действий, чем ре­ курсивный вызов процедуры. Из рассмотренного примера видно, что при прочих рав­ ных условиях рекурсивный алгоритм менее эффективен, чем циклический, и единственным его преимуществом является лаконичность записи.

А теперь рассмотрим рекурсивный алгоритм для решения головоломки «Ха­ нойские башни».

Пример 4.2. Задача «Ханойские башни». Имеется три вертикальных колышка, которые мы обозначим как a, b, c. На колышек a нанизано n круглых дисков раз­

ного диаметра, как в детской пирамидке: внизу расположен самый большой диск, вверху – самый малый. Требуется, перекладывая диски по одному, всю пирамидку переложить с колышка a на колышек c, используя колышек b, как вспомогатель­

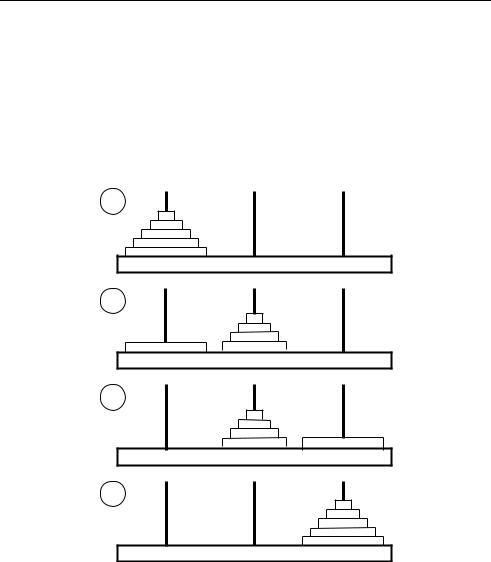
77

ный. При этом на любом промежуточном этапе нельзя нарушать правило башен: на любой диск можно сверху класть диск только меньшего размера.

Идея решения основывается на методе математической индукции.

Базис. Число дисков n=1. Переложить диск с колышка a на колышек c.

Предположение. Пусть алгоритм умеет перекладывать башни из n=k≥1. Индукция. Пусть n=k+1≥2. Перекладываем башню из k дисков с колышка a

на колышек b, затем один диск с колышка a на колышек c, и, наконец, башню из k дисков с колышка b на колышек c. Рис. 4.1 иллюстрирует процесс переклады­ вания дисков.

1

2

3

4

Рис. 4.1

Заметим, что переложить самый большой диск, находящийся внизу пирамидки на колышке a, на колышек c, не нарушая правило башен, можно только тогда, когда все остальные диски находятся на колышке b. Поэтому невозможно перело­ жить диски за меньшее количество перекладываний, чем это делает рассмотренный

алгоритм (4.2).

Для отладки алгоритма (4.2) в качестве процедуры ПЕРЕЛОЖИТЬ(x,y) можно использовать оператор вывода пары чисел x, y.

78

Глубина рекурсии при выполнении алгоритма (4.2) равна n, так как рекурсив­ ный вызов hanoi(n-1,b,a,c) происходит после окончания выполнения вызова hanoi(n-1,a,c,b).

procedure hanoi(n,a,b,c:integer); begin

if n=1 then ПЕРЕЛОЖИТЬ(a,c)

else begin (4.2) hanoi(n-1,a,c,b);

ПЕРЕЛОЖИТЬ(a,c); end;hanoi(n-1,b,a,c);

Подсчитаем количество перекладываний H(n) отдельных дисков, выполняемых алгоритмом. Анализ алгоритма позволяет построить рекуррентное соотношение:

из которого получаем:

H(n) = 2 H(n – 1) + 1 = 22H(n – 2) + 2 + 1 = 2n – 1 + 2n – 2 + … + 2 + 1 = 2n – 1. (4.2) Корректность формулы (4.2) легко доказывается методом математической индук­

Таким образом, количество перекладываний самым быстрым алгоритмом рас­ тет в геометрической прогрессии с ростом числа дисков. По одной из легенд, Бог, создав Вселенную, заставил джинна без устали решать эту задачу для 64 дисков, ска­ зав: когда джинн закончит свою работу, наступит конец света. Если предположить, что на каждое перекладывание джинн тратит одну секунду, то ему потребуется 264 с ≈ 1,8∙1017 с ≈ 580 млрд. лет.

Конец примера.

Рассмотрим рекурсивный алгоритм вычисления чисел Фибоначчи, задаваемых рекуррентной последовательностью (3.7).

Пример 4.3. Рекурсивный алгоритм вычисления чисел Фибоначчи:

function fib(n:integer):integer; begin

if n=0 then fib:=0

else if n=1 then fib:=1 (4.3) else fib:=fib(n-1)+fib(n-2)

end;

79

Глубина рекурсии при выполнении алгоритма (4.3) при n>0 равна n, так как рекурсивный вызов в строке fib(n-2) происходит после завершения вычисления fib(n-1). Для анализа трудоемкости алгоритма подсчитаем общее количество ре­ курсивных вызовов Rn. Из алгоритма видно, что числа Rn подчиняются следующе­ му рекуррентному соотношению:

Числа Rn растут даже быстрее, чем числа Фибоначчи, так что время вычисления оказывается огромным при больших n. Это происходит потому, что при вычислении

fib(n-2) не используются промежуточные результаты, полученные при вычисле­ нии fib(n-1).

Конец примера.

Из рассмотрения примера 4.3 можно сделать вывод о том, что если рекуррент­ ную последовательность можно вычислять с помощью цикла, то ее и следует вы­ числять с помощью цикла, но не рекурсии!

Пример 4.4. Задачу численного вычисления определенного интеграла функции одной переменной f (x) на интервале [a0, b0] с заданной точностью ε можно решить многими способами. Рассмотрим решение этой задачи методом трапеций с делением

В рассматриваемом методе предполагается, что если значение разности между S1 и S2 по абсолютной величине превышает долю ε, пропорциональную дроби (b – a) / (b0 – a0), то интервал [a, b] делится пополам, при этом интеграл на интервале [a, b] равен сумме интегралов на двух частях этого интервала. Таким образом, вы­ числения будем вести согласно рекуррентному соотношению:

где S1 и S2 вычисляются по формулам (4.4) и (4.5) соответственно.

Для исключения повторных вычислений в число параметров функции Int включим не только границы интервала, но и значение подынтегральной функции f на этих границах. Переменная e, задающая точность, будет глобальной. Глобальны­ ми будут также переменные a0 и b0, задающие границы интервала. Функция Int

80

реализует рекурсивный алгоритм (4.4) вычисления интеграла. Вызов этой функции для вычисления интеграла на интервале [a0, b0] будет следующим:

X:=Int(a0,b0,f(a0),f(b0));

function Int(a,b,fa,fb:real):real; var S1,S2,c,fc:real;

begin

c:=(a+b)/2; fc:=f(c);

S1:=(fa+fb)*(b-a)/2;

S2:=(fa+2*fc+fb)*(b-a)/4; (4.4) if abs(S1-S2)<e*(b-a)/(b0-a0)

then Int:=S2

else Int:=Int(a,c,fa,fc)+Int(c,b,fc,fb) end;

Глубина рекурсии при выполнении алгоритма (4.4) определяется количеством последовательных дроблений интервала пополам, так как второй рекурсивный вызов внутри функции происходит после завершения первого вызова. Если, например, ин­ тервал дробится на такие части, что размер самой малой из них в 220 ≈ 106 раз меньше исходного интервала, то все это выполняется всего за 20 последовательных дробле­ ний.

Для вычисления трудоемкости алгоритма в наихудшем подсчитаем общее коли­ чество рекурсивных вызовов при разбиении интервала на одинаковые части. Пусть

Соотношение (4.7) аналогично соотношению (4.1), его решение:

R(∆0) = 2 N – 1.

Нетрудно видеть, что общее количество вычислений подынтегральной функции всего на 2 больше, чем R(∆0).

Конец примера.

4.2 Рекурсивная сортировка слиянием

Использование рекурсии вполне оправданно тогда, когда дополнительные расхо­ ды памяти и увеличение времени работы алгоритма относительно невелики по срав­ нению с нерекурсивным вариантом. В качестве примера рассмотрим рекурсивный ал­