
mu
.pdf
4. Решите задачу Коши:
y y 9xe2 x , y(0) 0, y (0) 5.
5. Найдите общее решение системы дифференциальных уравнений:
x (t) 2x y,y (t) 9x 4 y.
6. Напишите пять первых членов ряда по известной формуле для обще-
го члена un |
|
|
|
|
2n |
|
и проверьте выполнение необходимого признака. |
||||||||||||
(n 1)! |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
7. Исследуйте числовые ряды на сходимость: |
|
|
|
|
|
|
|
||||||||||||
|
|
n 4 |
|
|
|
|
|
2n 1 |
|
|
|||||||||
7.1. |
|
|
|
|
|
|
|
; |
|
|
7.2. |
|
|
|
|
|
; |
|
|
n(n |
2 |
|
|
|
|
|
|
2 |
n |
|
|
|
|
||||||
n 1 |
|
3) |
|
|
n 1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
3 |
|
|
|
|
n |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7.3. |
|
|
|
|
|
|
|
; |
|
7.4. ( 1) |
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n 1 |
|
4n 1 |
|
|
|
|
n 1 |
|
|
|
n n |
|
|||||||
8. Найдите интервал сходимости степенного ряда. Исследуйте его поведение на концах интервала сходимости:
( x 5)n |
|
(n 1)! |
|
||||||||
8.1. |
|
|
|
; |
8.2. |
|
|
|
|
(x 2)n . |
|
|
n |
|
|
|
n |
|
|||||
n 1 |
n3 |
|
|
n 1 |
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
9. Разложите функцию |
y f (x) в ряд Тейлора в окрестности точки |
||||||||||
x a и укажите интервал сходимости полученного ряда: |
|||||||||||
9.1. y |
9x 1, a 0; |
9.2. y ln(3x 4), a 1; |
|||||||||
9.3. y cos2 |
2x, a ; |
9.4. y |
|
3 |
|
, a 2. |
|||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
3x |
|
|||
Вариант № 19
1. Найдите общее решение или общий интеграл дифференциального уравнения первого порядка:
|
|
|
|
|
|
|
|
y e 2 y x |
y |
; |
|||
1.1. y y 1 x2 x 1 y2 0; |
1.4. |
||||||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
||||
|
|
|
|
y y cos x |
1 |
sin 2x. |
|||||||
1.2. y2 2dx ydy x2 ydy ; |
1.5. |
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|||
71

1.3.y 2 y2 3y ;
x2 x
2. Решите задачу Коши:
y |
y |
|
ln x |
, |
y(1) 1. |
|
x |
x |
|||||
|
|
|
|
3. Найдите общее решение дифференциального уравнения:
3.1. y |
|
4 |
; |
3.4. 16y 8y y 0 ; |
|
|
|||
3 |
x4 |
|
||
3.2. 4 y 3y y 0; |
3.5. y 3y 2y e3x (3 4x) . |
|||
3.3. 4 y y 0 ; |
|
|||
4. Решите задачу Коши: |
|
|||
|
|
|
y y x 1, |
y(0) 0, y (0) 2. |
5. Найдите общее решение системы дифференциальных уравнений:
x (t) x 2 y,y (t) x y.
6. Напишите пять первых членов ряда по известной формуле для обще-
го члена u |
|
|
( 1)n n |
и проверьте, выполнение необходимого признака. |
|||||||
n |
|
2n |
|||||||||
|
|
|
|
|
|
|
|
|
|||
7. Исследуйте числовые ряды на сходимость: |
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
4n |
2n |
||
|
|
|
|
|
|||||||
7.1. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
; |
7.2. |
|
|
; |
||
|
1) |
2 |
|
|
|||||||
n 1 (2n |
|
4 |
n 1 |
|
3n 1 |
|
|||||
|
2 |
|
|
ln(n 1) |
|
7.3. |
n |
; |
7.4. ( 1)n |
. |
|
n |
|
||||
n 1 |
3 |
|
n 1 |
n 1 |
|
8. Найдите интервал сходимости степенного ряда. Исследуйте его поведение на концах интервала сходимости:
|
( x 1)n |
|
(n 1)(x 3)n |
|||
8.1. |
|
|
; |
8.2. |
|
. |
n2 |
n |
|
||||
n 1 |
|
|
n 1 |
n! |
||
|
|
|
|
|
||
72

9. Разложите функцию y f (x) |
в ряд Тейлора в окрестности точки |
|||||||||
x a и укажите интервал сходимости полученного ряда: |
||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9.1. y e2 , a 1; |
|
9.2. y ln(4 x), a 0; |
||||||||
|
|
|
2 |
|
|
|
|
|
1 |
|
9.3. y sin |
|
x |
|
, a ; |
9.4. y |
|
|
, a 2. |
||
|
|
4x |
||||||||
|
|
|
|
|
4 |
|
3 |
|
||
Вариант № 20
1. Найдите общее решение или общий интеграл дифференциального уравнения порядка:
|
|
|
|
|
|
|
|
|
1.4. y y ctg x cos2 x ; |
||||||
1.1. (e 3x 3)dy |
|
y 4e 3xdx 0; |
|
||||||||||||
1.2. xdx 4 ydy 5x2 ydy xy2dx ; |
|
1.5. y |
y |
3y |
2 x. |
||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1.3. y |
y2 |
|
y |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2x2 |
9x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Решите задачу Коши: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
y |
2 y |
(x 1)3 |
, |
y(1) |
1 |
. |
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x 1 |
|
2 |
|
|
|
|
||
3. Найдите общее решение дифференциального уравнения: |
|
||||||||||||||
3.1. y cos3x ; |
|
|
|
|
|
|
3.4. 16 y 9 y 0 ; |
||||||||
3.2. y 5y 6y 0 ; |
|
3.5. y 4y 4y 2sin x . |
|||||||||||||
3.3. 9 y 6 y y 0 ;
4. Решите задачу Коши:
y 6 y 9 y e3x , y(0) 1, y (0) 0.
5. Найдите общее решение системы дифференциальных уравнений:
x (t) x 2 y,y (t) 3x 4 y.
6. Напишите пять первых членов ряда по известной формуле для обще-
( 1)n 1
го члена un и проверьте выполнение необходимого признака. n!
73

7. Исследуйте числовые ряды на сходимость:
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
1 |
|
|
n |
|
2 |
|
|
|||||
|
|
|
|
|
|
|||||||||
7.1. |
|
|
|
; |
7.2. |
|
|
|
|
|
; |
|
||
|
|
|
|
|
|
|
||||||||
n 1 |
n(n 4) |
|
n 1 |
4n 3 |
|
|
|
|
||||||
|
n3 |
|
|
|
|
|
|
2n |
|
|||||
7.3. |
|
|
; |
|
7.4. ( 1)n |
|
|
|
|
|
. |
|||
4 |
n |
|
3n |
2 |
5 |
|||||||||
n 1 |
|
|
|
n 1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. Найдите интервал сходимости степенного ряда. Исследуйте его поведение на концах интервала сходимости:
|
2 |
( x 3) |
n |
|
n!(x 2) |
n |
|||
8.1. |
n |
|
|
; |
8.2. |
|
. |
||
|
|
2n 1 |
|
n |
|
||||
n 1 |
|
|
|
n 1 |
|
|
|||
|
|
|
|
|
|
|
|||
9. Разложите функцию |
y f (x) в ряд Тейлора в окрестности точки |
||||||||
x a и укажите интервал сходимости полученного ряда:
9.1. y e 3x , a 1; |
|
9.2. y ln(3 x), a 2; |
|||||||
|
|
|
|
|
|
1 |
|
|
|
9.3. |
y cos |
3x |
|
, a 0; |
9.4. y |
|
|
, a 2. |
|
2x 5 |
|||||||||
|
|
|
4 |
|
|
|
|||
4.2.4. Решение типового варианта и образец оформления индивидуального задания № 2
Вариант № 0
Задача 1. Найдите общее решение или общий интеграл дифференциального уравнения порядка:
|
|
|
|
|
|
|
y |
e |
|
y |
||||
1.1. y(e4 x 1)dy |
4 y2 e4 xdx 0; |
1.4. y |
|
|
|
|
||||||||
2 x ; |
||||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
1.2. |
y |
y |
xsin x; |
|
|
1.5. y |
4 y2 |
|
|
3y |
. |
|||
x |
|
|
x2 |
|
||||||||||
|
|
|
|
|
|
|
|
x |
||||||
1.3.2xdx ydy x2 ydy 3xy2dx ;
Решение
|
|
|
1.1. y(e4 x 1)dy |
4 y2 e4 xdx 0 |
|
Это дифференциальное уравнение первого порядка является уравнением с разделяющимися переменными. Разделим переменные, для этого выполним следующие преобразования:
второе слагаемое в левой части уравнения перенесем в правую часть
y(e4 x 1)dy 
 4 y2 e4 xdx ;
4 y2 e4 xdx ;
74
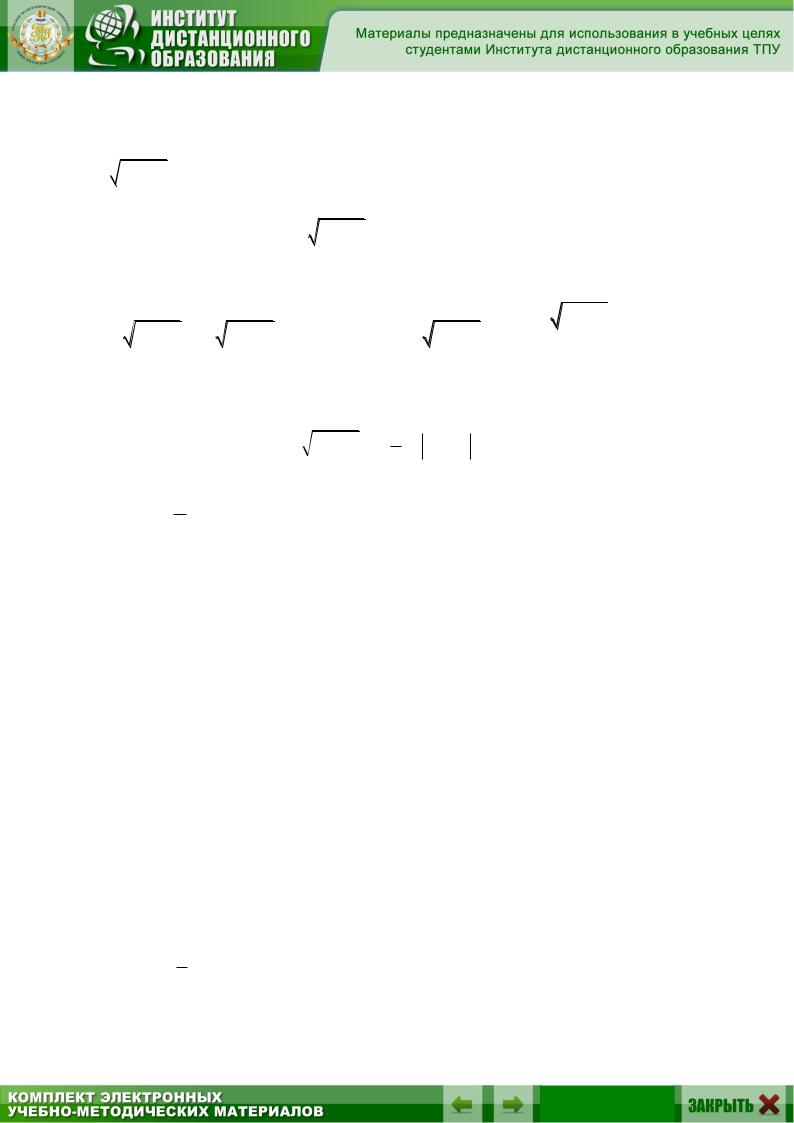
путем деления избавимся в левой части уравнения от множителя (e4 x 1) , зависящего от x , а в правой части уравнения от множителя

 4 y2 , зависящего от y
4 y2 , зависящего от y
y |
dy |
e4 x |
|
dx. |
|
4 y2 |
e4 x 1 |
||||
|
|
||||
Вычислим теперь интегралы от выражений, стоящих в левой и правой частях уравнения:
|
ydy |
|
|
|
y |
|
|
d (4 y2 ) |
|
|
1 |
|
d (4 y2 ) |
|
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
4 y2 |
C; |
||||||||||||||||||||||
4 y2 |
|
4 y2 |
( 2 y) |
|
|
2 |
4 y2 |
2 |
|
||||||||||||||||||||||
|
|
e4 xdx |
|
|
e4 x |
d (e4 x 1) |
|
1 |
|
d (e4 x 1) 1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
e4 x 1 |
|
C. |
|
|||||||||||||||
e4 x 1 |
e4 x 1 |
|
4e4 x |
4 |
|
e4 x 1 |
4 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Таким образом, общий интеграл уравнения имеет вид

 4 y2 14 ln e4 x 1 C.
4 y2 14 ln e4 x 1 C.
1.2. y xy xsin x
Это дифференциальное уравнение первого порядка является линейным, так как функция y и её производная y содержатся только в
первой степени. Для его решения воспользуемся методом подстановки.
Будем искать решение уравнения |
в |
виде y u(x) v(x). |
Тогда |
|||||||
y u (x)v(x) u(x)v (x) . Подставим y |
и |
y u (x)v(x) u(x)v (x) |
в ис- |
|||||||
ходное уравнение. Получим |
|
|
|
|
|
|
|
|
|
|
u v uv |
uv |
xsin x. |
|
|||||||
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
||
Сгруппируем второе и третье слагаемые в левой части уравнения и |
||||||||||
вынесем общий множитель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
u v u v |
|
|
|
|
|
xsin x. |
|
|||
|
|
|
|
|||||||
|
|
|
|
|
x |
|
|
|
|
|
Составим систему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
v |
|
|
|
|
0, |
|
|
|||
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
u v x sin x.
Решим первое уравнение системы и найдём функцию v : v vx 0 ;
75

dvdx vx ; dvv dxx ;
dvv dxx ; ln v ln x ;
v x .
Подставим функцию v во второе уравнение системы и решим полученное уравнение:
u x xsin x ; u sin x ; dudx sin x ; du sin xdx ;
du sin xdx ;
u cos x C.
Таким образом, общее решение уравнения будет иметь вид
y(cos x C)x.
1.3.2xdx ydy x2 ydy 3xy2dx
Это дифференциальное уравнение первого порядка является уравнением с разделяющимся переменными. Перенесем все слагаемые из правой части уравнения в левую и сгруппируем слагаемые с dx и dy :
2xdx ydy x2 ydy 3xy2dx 0; (2x 3xy2 )dx ( y x2 y)dy 0; x(2 3y2 )dx y(1 x2 )dy 0.
Перенесем второе слагаемое из левой части уравнения в правую и разделим переменные:
x(2 y2 )dx y(1 x2 )dy;
xdx |
|
ydy |
. |
|
1 x2 |
2 3y2 |
|||
|
|
Найдем интегралы от левой и правой частей уравнения:
|
xdx |
|
x |
|
d (1 x2 ) |
|
1 |
|
d (1 x2 ) |
|
1 |
ln |
|
1 |
x2 |
|
C, |
|
|
||||||||||||||||
1 x2 |
1 x2 |
2x |
2 |
1 x2 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
76
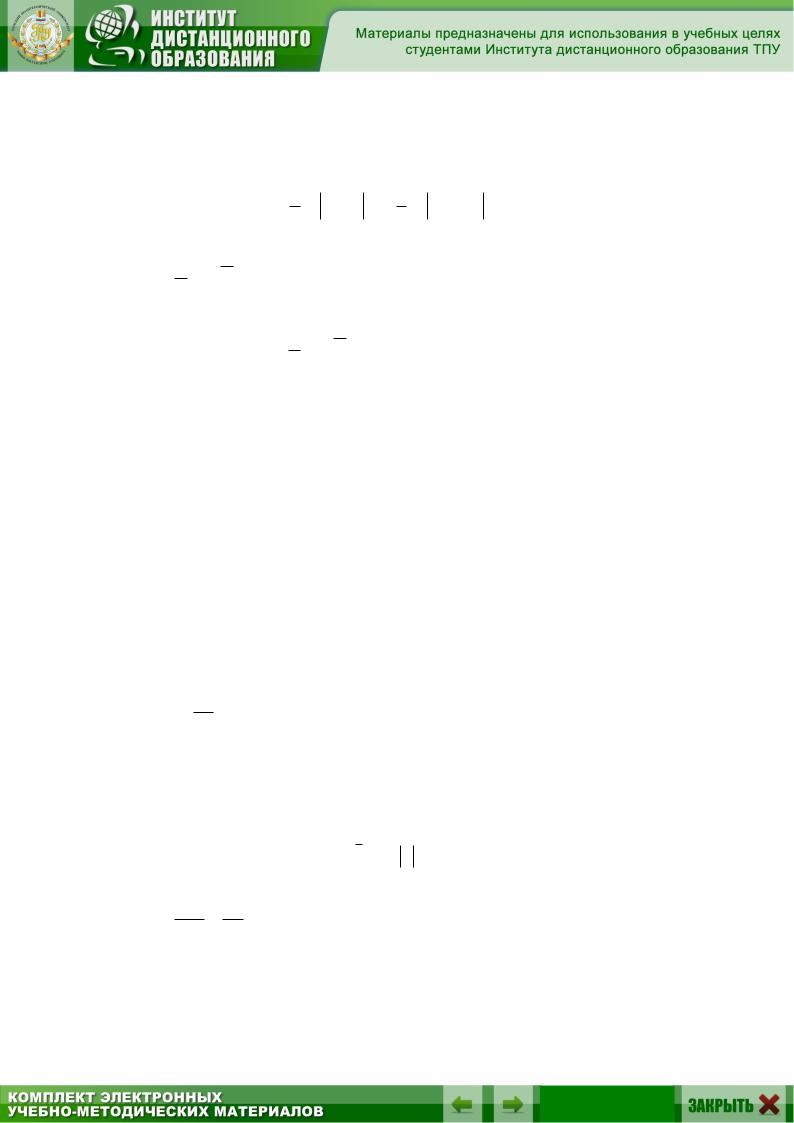
|
ydy |
|
y |
|
d (2 3y2 ) |
|
1 |
|
d (2 3y2 ) |
|
1 |
ln |
|
2 |
3y2 |
|
C. |
|
|
||||||||||||||||
2 3y2 |
2 3y2 |
6 y |
6 |
2 3y2 |
6 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Запишем общий интеграл уравнения:
12 ln 1 x2 16 ln 2 3y2 C.
1.4.y xy e 2yx
Данное дифференциальное уравнение является однородным, так
как функция f (x, y) xy e 2yx является однородной функцией нулевого измерения. Действительно,
|
f ( x, y) y |
e |
y |
y |
e |
y |
|||||||||||
|
2 x |
|
2 x |
f (x, y). |
|||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
x |
||||||
С помощью подстановки y tx, y t x t , где t t(x) сведём урав- |
|||||||||||||||||
нение к уравнению с разделяющимися переменными: |
|||||||||||||||||
|
|
|
|
|
tx |
e |
tx |
|
|
|
|
|
|
|
|||
t x t |
x |
|
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
t x t t e t ; |
|
|
|
|
|
|
|
||||||||||
t x e t ; |
|
|
|
|
|
|
|
||||||||||
|
dt |
|
x e t ; |
|
|
|
|
|
|
|
|||||||
|
dx |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dt |
|
|
dx |
; |
|
|
|
|
|
|
|
|||||
|
e t |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
|
|
|
|
|
|
|||||||
et dt dxx .
Найдем интегралы от левой и правой частей последнего равенства:
et dt et C e |
y |
|
|
dx |
|
|
|
|
x |
C ; |
|
ln |
x |
C. |
|||
x |
||||||||
|
|
|
|
|
|
|
Запишем общий интеграл уравнения:
y
e x ln x C.
1.5.y 4 y2 3y
x2 x
77

Это дифференциальное уравнение первого порядка является одно-
родным, так как функция |
f (x, y) |
4 y2 |
|
|
|
3y |
является однородной функ- |
||||||
|
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
||
цией нулевого измерения. Действительно, |
|
||||||||||||
f ( x, y) |
4( y)2 |
|
3 y |
4 |
y2 |
|
|
3y |
|
f (x, y). |
|||
( x)2 |
x |
x2 |
|
|
x |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
Для решения уравнения используем следующую подстановку:
y t x , где t t(x), |
y t x t. |
В результате указанной подстановки уравнение принимает вид:
t x t |
4t2 x2 |
|
3tx |
или t x t t2 3t. |
|
x2 |
x |
||||
|
|
|
Откуда
t x 4t2 4t .
Последнее уравнение является дифференциальным уравнением с разделяющимися переменными. Учитывая, что t dxdt , получаем:
dt |
x 4t2 4t ; |
||||
dx |
|||||
|
|
|
|
||
|
dt |
|
dx |
. |
|
4t2 4t |
|
||||
|
x |
||||
Вычислим интегралы от левой и правой частей уравнения:
|
|
|
|
|
dt |
|
|
|
|
|
|
|
4t2 4t 4t2 4t 1 1 |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
1 d (2t 1) |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(2t 1)2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
4t2 4t |
|
|
|
|
|
|
|
|
|
|
(2t 1)2 1 |
2 |
(2t 1)2 1 |
||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
2t 1 1 |
|
C |
1 |
|
|
|
2t 2 |
|
|
C |
1 |
ln |
|
|
t 1 |
|
|
C |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
ln |
|
|
|
ln |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2t 1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 2 |
|
|
|
|
|
4 |
|
|
|
|
|
2t |
|
|
|
4 |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
y |
1 |
|
|
1 |
|
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ln |
|
|
|
|
|
|
|
C |
|
ln |
|
|
|
|
|
|
|
C, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4 |
|
y |
x |
4 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ln |
|
x |
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Запишем общий интеграл уравнения: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
y x |
|
ln |
|
|
|
C. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
y |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78

Задача 2. Решите задачу Коши:
y |
y |
|
2ln x |
, |
y(1) |
1 |
. |
|
x |
x |
2 |
||||||
|
|
|
|
|
Решение
Это дифференциальное уравнение первого порядка является линейным относительно неизвестной функции y. Будем его решать с по-
мощью подстановки
y u(x)v(x), y u (x)v(x) u(x)v (x).
Подставим y |
и y u (x)v(x) u(x)v (x) в исходное уравнение. По- |
|||||||||||||||||||||||||||||||||||
лучим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
u v uv |
|
uv |
|
|
2ln x |
. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
||||||
Сгруппируем второе и третье слагаемые в левой части уравнения и |
||||||||||||||||||||||||||||||||||||
вынесем общий множитель u за скобки: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
2ln x |
|
|||||||||||
u v u v |
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||
|
x |
x |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Запишем систему уравнений: |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
v |
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2ln x |
|
|
|
|
|
|
|
|
||||||||||||||||
u v |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решим первое уравнение системы: |
||||||||||||||||||||||||||||||||||||
v |
v |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dv |
|
|
v |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dv |
|
|
dx |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
dv |
|
dx |
; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ln |
|
v |
|
ln |
|
x |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ln |
|
v |
|
ln |
x 1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
v x 1 или v |
|
. |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||
Подставим функцию v во второе уравнение системы и найдём функцию u :
79

u 1 2ln x ; x x
u 2ln x ;
dudx 2ln x ; du 2ln xdx ;
du 2 ln xdx .
Интеграл в правой части последнего равенства вычислим методом интегрирования по частям
2 ln xdx 2 x ln x dx 2 x ln x x C .
Получаем
u 2 xln x x C .
Общее решение уравнения будет иметь вид: y uv 2 x ln x x C 1x .
Найдём теперь частное решение, используя начальное условие y(1) 12 . Для этого подставим в общее решение значения x 1 и y 12
и найдём С:
12 2 1 ln1 1 C 11 12 2 C ;
C 32 .
Тогда частное решение уравнения имеет вид
|
2 x ln x x |
3 |
|
|
1 |
|
y |
|
|
|
|
. |
|
|
|
|||||
|
|
2 |
|
|
x |
|
Задача 3. Найдите общее решение дифференциального уравнения:
|
|
|
|
3.1. y 3cos2x x ; |
3.4. 16 y y 0 ; |
||
3.2. y 5y 6y 0 ; |
3.5. y 2 y 3y 2ex . |
||
3.3. 25y 10 y y 0 ; |
|
||
80
