
- •Оглавление
- •Предисловие
- •Языки
- •Грамматики
- •Автоматы
- •Эквивалентность ДКА и НКА
- •Минимизация конечных автоматов
- •Регулярные выражения
- •Регулярные грамматики
- •Замкнутость класса регулярных языков
- •Лемма о расширении регулярных языков
- •Контекстно-свободные грамматики
- •Грамматический разбор
- •Неоднозначность грамматик и языков
- •Методы преобразования грамматик
- •Нормальные формы КС-грамматик
- •Магазинные автоматы
- •Недетерминированные магазинные автоматы
- •Магазинные автоматы и КС-языки
- •Лемма о расширении
- •Предметный указатель

Конечные автоматы |
|
Лекция |
|
|
2 |
Автоматы
Автомат можно рассматривать как упрощенную абстрактную модель компьютера. Он имеет способность воспринимать входную информацию, которую мы будем представлять в
виде строки символов в фиксированном алфавите и которую автомат может лишь читать, но не может изменять. Предполагается, что входная строка записана на ленте, разделенной на клеточки, каждая из которых может содержать не более одного символа. Автомат может различать конец входной строки (например, отмеченный специальным символом) и реагировать на прочитанную информацию тем или иным способом. У него может быть
устройство временной памяти, содержащее потенциально неограниченное число ячеек, в каждую из которых может быть записано не более одного символа из некоторого алфавита (вообще говоря, не совпадающего с входным). Автомат может читать и изменять содержимое ячеек временной памяти. Наконец, автомат имеет устройство управления, которое может находиться в одном из конечного множества внутренних состояний и изменять его по мере необходимости.
Свойства автомата самым существенным образом зависят от характера временной памяти. Предполагается, что автомат функционирует в дискретном времени. В каждый момент времени устройство управления находится в некотором внутреннем состоянии, а читающая головка обозревает очередной символ на входной ленте. В следующий момент времени устройство управления переходит в некоторое новое состояние в зависимости от предыдущего состояния, прочитанного символа на входной ленте и содержимого временной памяти.
Лекция 2 |
15 |
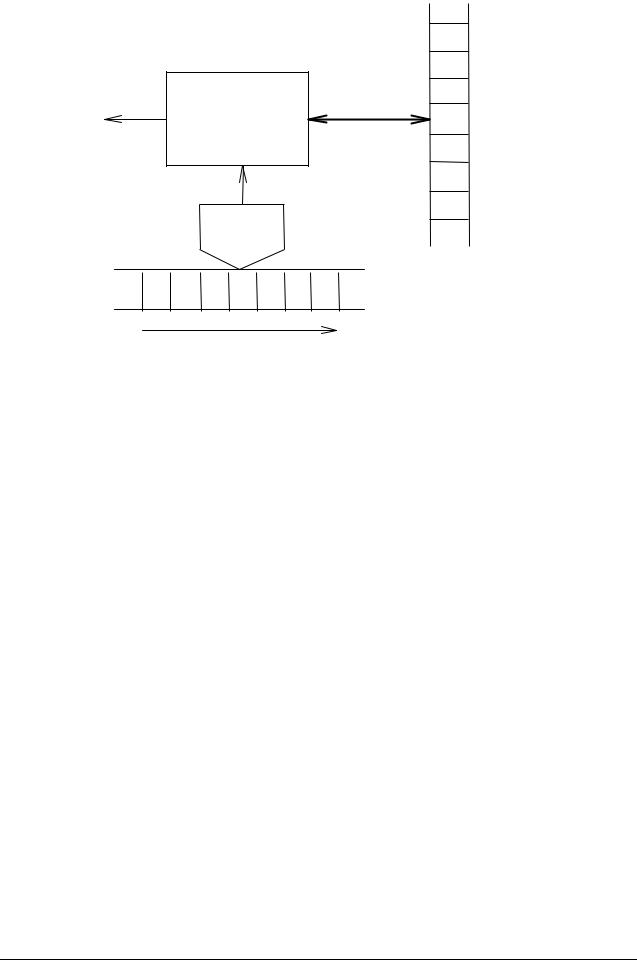
Устройство |
|
|
Выход |
А |
Временная |
управления |
B |
память |
C
Читающая
головка
a a b b Входная лента
Направление чтения
Рис. 2.1. Схема автомата
Это соответствие задает функцию перехода автомата, которая определяет его возможное поведение. В результате перехода автомата из одного состояния в другое может появиться выходная информация или может быть записана новая информация во временную память.
Состояние устройства управления, прочитанный входной символ и содержимое временной памяти определяют то, что называется конфигурацией автомата в данный момент времени. Переход от одной конфигурации в момент времени t к другой конфигурации в момент t + 1 называется шагом. Таким образом, функционирование автомата состоит из последовательности шагов (конечной или бесконечной). Различают два типа автоматов:
детерминированные и недетерминированные. Поведение детерминированного автомата в каждый следующий момент времени полностью предопределено его внутренним состоянием в предыдущий момент, прочитанным символом и содержимым временной памяти, т.е. если автомат может совершить следующий
16 |
Конечные автоматы |

шаг, то он будет единственно возможным шагом. Для недетерминированного автомата это не так: в каждый следующий момент времени автомат может выбрать шаг из некоторого (конечного) множества шагов. Таким образом, для недетерминированного автомата мы можем лишь предполагать тот или иной возможный вариант функционирования. Между детерминированными и недетерминированными автоматами существуют интересные с точки зрения формальных языков связи.
Автомат, выход которого ограничен двумя сообщениями {да, нет}, называется распознавателем. Реагируя на входную строку, распознаватель или распознает ее (допускает), или отвергает. Этот класс автоматов представляет наибольший интерес с точки зрения формальных языков и грамматик. Автомат более общего типа, выдающий на выходе целую строку символов, называется преобразователем (этот тип автоматов не изучается в нашем курсе).
Пример 2.1.
Рассмотрим грамматику GI , порождающую подъязык идентификаторов LI в языке Паскаль:
GI: <идентификатор> → <буква> <хвост> | <буква><буква> , <хвост > → <буква> <хвост> | <цифра> <хвост> | <цифра>, <буква> → a | b | c | ... | A | B | ... | Z
<цифра> → 0 | 1 | 2 | ... | 9
Здесь N = {<идентификатор>, <буква>, <цифра>, <хвост>},
T = {a, b, ..., A, B, ..., Z, 0, 1, 2, ..., 9, ε}, S = <идентификатор>.
Вывод идентификатора А1 выглядит так:
<идентификатор> <буква><хвост> A<хвост> A<цифра> A1.
Лекция 2 |
17 |
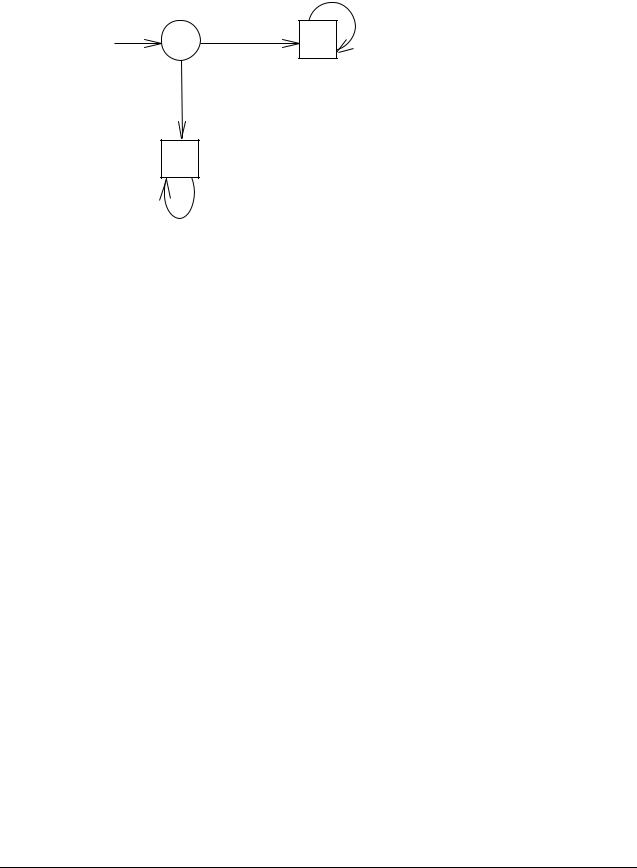
Построим автомат, распознающий только язык LI и никакой другой:
Пуск |
буква |
буква |
|
Да |
или |
|
цифра |
цифра |
|
|
Нет
буква
или
цифра
Рис. 2.2. Автомат, распознающий язык LI
Детерминированные конечные
автоматы (распознаватели)
Рассмотрим самый простой случай, когда у автомата отсутствует дополнительная временная память, устройство управления может находиться в одном из конечного множества состояний,
а реакция на входную строку выражается ответами «да» или «нет».
Определение 2.2.
Детерминированный конечный автомат (распознаватель), или сокращенно ДКА, – это пятерка
M = (Q, Σ, θ, q0, F),
где:
Q – конечное множество внутренних состояний;
18 |
Конечные автоматы |

Σ – конечное множество символов, называемое входным алфавитом;
θ: Q × Σ → Q – всюду определенная функция, называемая
функцией переходов; q0 Q – начальное состояние;
F Q – множество заключительных состояний.
В дальнейшем под ДКА мы будем понимать только детерминированный конечный распознаватель. ДКА функционирует следующим образом. В начальный момент времени, находясь в состоянии q0, он с помощью читающей головки обозревает самый левый символ входной строки. Головка читает строку слева направо, без возвратов, сдвигаясь вправо на один символ за каждый шаг работы автомата. В соответствии с заданной функцией переходов автомат изменяет свои внутренние состояния в процессе чтения входной строки. Прочитав ее до конца, автомат оказывается либо в одном из заключительных состояний (и в этом случае строка будет допущена или распознана автоматом), либо в каком-то другом, не заключительном (и в этом случае строка отвергается).
Для наглядного представления функционирования автомата используются диаграммы переходов. Это ориентированные конечные графы, в которых вершины соответствуют внутренним состояниям автомата (и помечаются соответствующими символами).
Если M = (Q, Σ, θ, q0, F) – ДКА, тогда его диаграмма переходов – это граф DM, имеющий ровно |Q| вершин, каждая из которых помечена некоторым qi Q. Для каждого правила перехода θ(qi, a) = qj в DM существует дуга (qi, qj), помеченная символом a. Вершина, помеченная q0, называется начальной, а те вершины, метки которых qf F, называются финальными (или заключительными). Финальные вершины будем изображать квадратиками, а нефинальные - кружочками.
Лекция 2 |
19 |
Нетрудно видеть, что определения ДКА с помощью пятерки (Q, Σ, θ, q0, F) и посредством диаграммы переходов DM равносильны.
Полезно ввести обобщенную функцию переходов
θ*: Q × Σ* → Q.
Вторым аргументом у θ* является не отдельный символ, а целая строка, а значение функции указывает на то внутреннее состояние, в котором окажется автомат после серии переходов в результате чтения этой строки.
Пример 2.3.
Рассмотрим ДКА
M = ({q0, q1, q2}, {a, b}, θ, q0, {q1}),
где θ(q0, a) = q0 , |
θ(q0, b) = q1, |
θ(q1, a) = q0 , |
θ(q1, b) = q2, |
θ(q2, a) = q2 , |
θ(q2, b) = q1. |
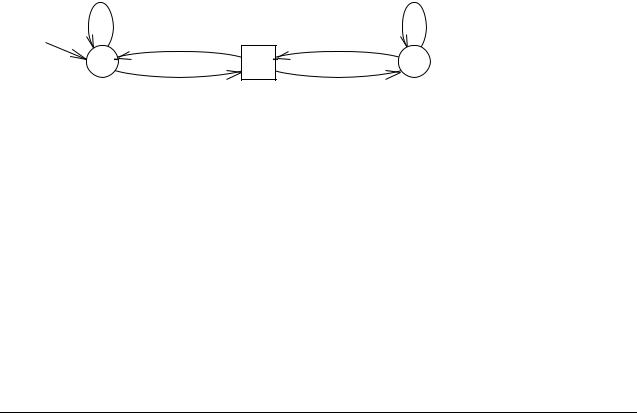
Ему соответствует диаграмма DM:
a |
a |
a |
|
b |
q0 |
q1 |
q2 |
b |
|
b |
Этот автомат распознает строки ab, bab, abbb, bbaab, но отвергает baa или bbaa.
В заключение дадим рекурсивное определение функции θ*:
θ*(q, ε) = q,
θ*(q, αa) = θ(θ*(q, α), a) для всех q Q, α Σ*, a Σ.
20 |
Конечные автоматы |
Языки и детерминированные конечные
автоматы
Дадим теперь строгое определение языка, связанного с конкретным ДКА.
Определение 2.4.
Язык, допустимый ДКА M = (Q,Σ,θ,q0,F), – это множество всех строк из Σ*, допустимых автоматом М, т.е. L(M) = {α | α Σ* и
θ*(q0, α) F}.
Так как функции θ и θ* являются всюду определенными и каждый шаг работы автомата определяется единственным образом, то любая строка α Σ* после прочтения ее либо допускается (распознается) автоматом, либо отвергается им. Отсюда следует, что
L(M) = {α | α Σ* и θ*(q0, α) F}.
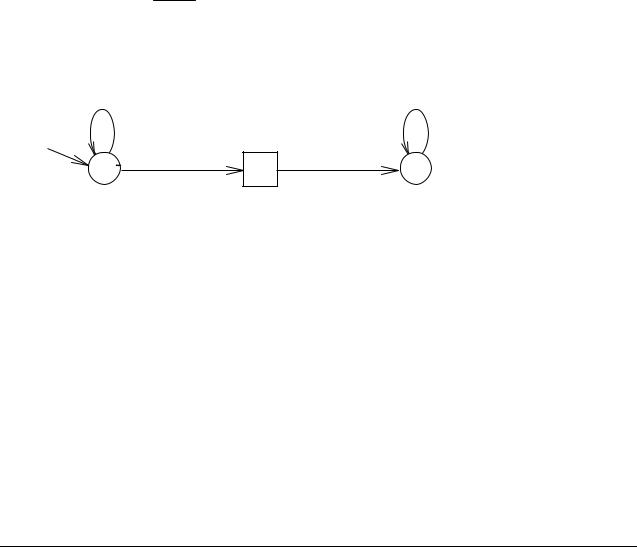
Пример 2.5.
a |
|
|
|
a, b |
q0 |
b |
q1 |
a, b |
q2 |
Этой диаграмме соответствует ДКА, допускающий язык L = {anb| n ≥ 0}.
Теорема 2.6.
Пусть M = (Q, Σ, θ, q0, F) – детерминированный конечный автомат (распознаватель) и пусть DM – соответствующая диаграмма пе-
реходов. В этом случае для любых qi, qj Q и α Σ + θ*(qi, α) = qj тогда и только тогда, когда в DM существует путь, помеченный
последовательностью символов α, из вершины qi в вершину qj.
Доказательство.
Лекция 2 |
21 |

Проведем его индукцией по длине строки α.
Пусть |α| = 1, т.е. α = а для некоторого a Σ. Тогда θ*(qi, α) = θ(qi, а) = qj, по определению, соответствует дуге (qi, qj), помеченной а, в DM. Допустим, что для всех α таких, что |α| ≤ n, утверждение верно. Пусть |α| = n + 1, и пусть θ*(qi, α) = qj. Можно положить α = βа, где |β| = n. Тогда для некоторого qk
θ*(qi, β) = qk и θ*(qi, α) = θ(qk, a) = qj.
По предположению, равенство θ*(qi, β) = qk эквивалентно существованию пути в DM из qi в qk, помеченному β. Кроме того, соотношение θ*(qk, a) = qj эквивалентно существованию дуги (qk, qj) с меткой а, что дает нам в DM путь из qi в qj, проходящий через вершину qk и помеченный строкой βa, который соответствует
соотношению θ*(qi, α) = |
qj. Теорема доказана. |
|
|
|||
Функция θ может быть задана таблицей: |
|
|
||||
|
a1 |
a2 |
... |
ak |
... |
an |
|
||||||
|
|
|
|
|
|
|
q0 |
|
|
|
|
|
|
q1 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
qi |
|
|
|
qj |
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
q |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь на пересечении i-й строки и k-го столбца находится qj тогда и только тогда, когда θ(qi, ak) = qj.
22 |
Конечные автоматы |
Если функция θ не всюду определенная, то ее можно доопределить так, что соответствующий автомату язык не изменится.
Для любой пары (q, a), для которой θ(q, a) не определено, положим θ(q, a) = ∆, где ∆ Q Σ. Кроме того, для любого а Σ положим θ(∆, a) = ∆.
При этом функция θ становится всюду определенной. Так как ∆ Q, то ∆ F, а отсюда следует, что для любой строки α Σ* α L(M) тогда и только тогда, когда в модифицированном ДКА М∆ θ*∆(q0, α) F, что означает, что α L(M∆). Следовательно, L(M) =
L(M∆).
Пример 2.7.
|
|
b |
a, b |
|
a |
|
|
q0 |
q1 |
|
∆ |
b |
a |
a |
b |
q2 |
q3 |
q4 |
a |
|
b |
b |
a |
У приведенного на диаграмме автомата функция переходов не является всюду определенной. Вводя новое состояние ∆, являющееся «ловушкой», мы доопределяем эту функцию (достройка диаграммы показана штрихами).
Определение 2.8.
Язык L называется автоматным, если существует ДКА М такой, что L = L(M).
Таким образом, семейство всех ДКА определяет класс автоматных языков.
Лекция 2 |
23 |
Конечные автоматы
Лекция
3
Недетерминированные конечные автоматы (распознаватели)
ОпределениеНедетерминированный3.1. конечный автомат (распознаватель),
или НКА, – это пятерка М = (Q, Σ, θ, q0, F), где Q, Σ, q0, F определяются так же, как и для ДКА, а функция переходов θ выглядит так:
θ: Q × (Σ {ε}) → 2Q.
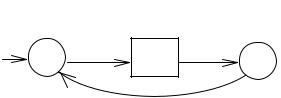
Пример 3.2.
q0 |
b |
а,b |
q2 |
q1 |
|||
|
а |
|
|
|
ε |
|
|
Заметим, что здесь
θ(q0, a) = {q0}, θ(q0, b) = , θ(q1, a) = {q2},
значит, это НКА.
θ(q1, b) = {q0, q2}, θ(q0, a) = , θ(q0, b) = ,
24 |
Конечные автоматы |
Определение 3.3.
Для НКА обобщенная функция переходов θ* определяется следующим образом: для любых qi, qj Q и α Σ* θ*(qi, qj)
содержит qi тогда и только тогда, когда в диаграмме переходов этого НКА существует путь из qi в qj, помеченный α.
Определение 3.4.
Язык, допускаемый НКА М, определяется так:
L(M) = {α | α Σ* и θ*(q0,α) ∩ F = }.
Пример 3.5.
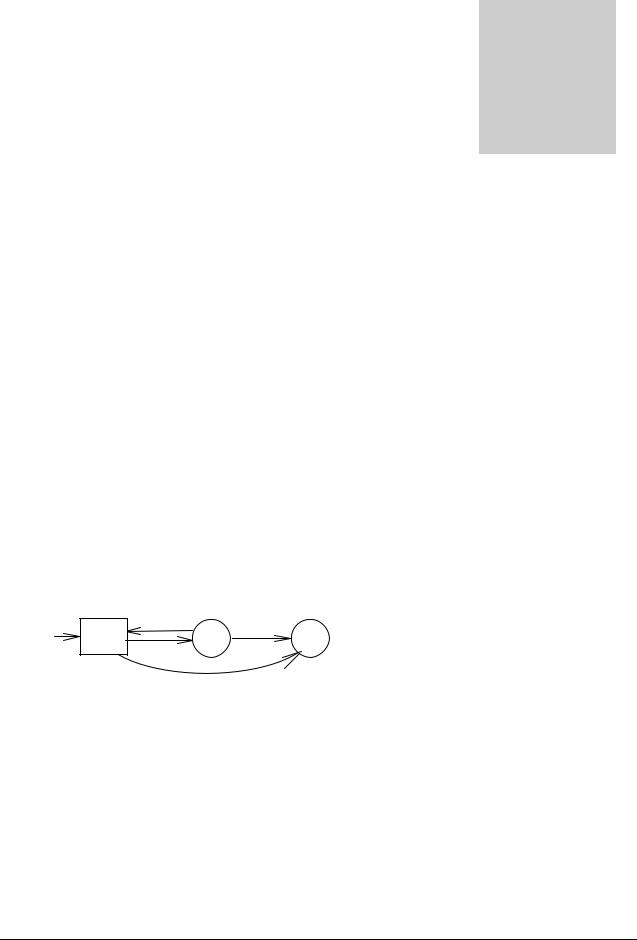
Рассмотрим НКА, заданный диаграммой:
q0 a |
q1 |
ε q2 |
ε
Вычислим θ*(q1, а) и θ*(q2, ε).
Рассмотрим сначала все пути из q1, соответствующие прочитанному символу а: {εεa(q1), εεaε(q2), εεaεε(q0)}. В круглых скобках указаны вершины, в которых оканчиваются эти пути. Тогда, по определению,
θ*(q1, а) = {q0, q1, q2}.
Аналогично
θ*(q2, а) = {q0, q2}.
Заметим, что для любого q: q θ*(q, ε).
От НКА М, содержащего ε-переходы, можно перейти к М' без ε-переходов так, что L(M) = L(M'). Для этого нужно для каждой пары (qi, а), qi θ, a Σ, определить множество всех путей вида
α = ε ε ... ε а ε ... ε,
выходящих из вершины qi, и сформировать множество всех вершин qj1, ..., qjk, которыми оканчиваются эти пути.
Лекция 3 |
25 |
|
Вводим новую функцию переходов θ' для НКА М':
θ'(qi, а) = {qj1, ..., qjk},
и полагаем
М' = (Q, Σ, θ', q0, F).
Нетрудно видеть, что при этом
L(M) = L(M').
Это дает нам возможность в дальнейшем, при рассмотрении
НКА как средства задания языков, считать, что НКА не содержит ε-переходов, т. е. θ: Q х Σ → 2Q.
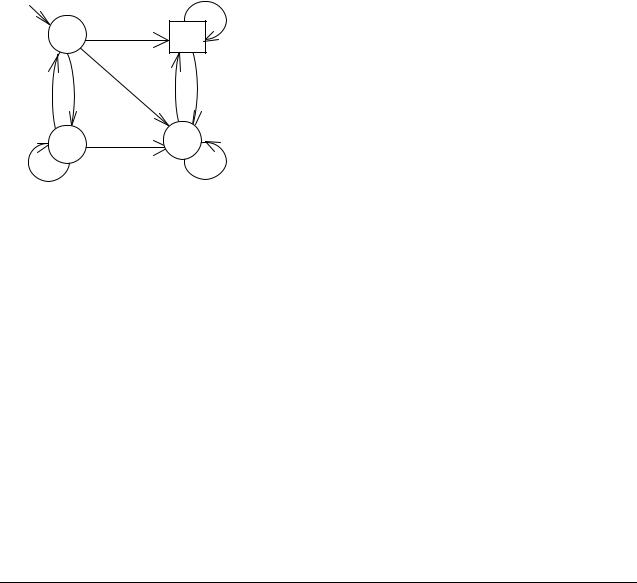
Пример 3.6.
Рассмотрим НКА М, заданный диаграммой DМ:
q0 |
a, ε |
q1 |
b |
Здесь Q = {q0, q1, q2, q3}, |
a ε |
b |
b |
a |
Σ ={a, b}, F = {q1}. |
|
||||
q2 |
b |
q3 |
|
|
b |
|
a |
|
|
Построим автомат (недетерминированный) М' = (Q, Σ, q0', θ', F') без ε-переходов и такой, что L(M) = L(M'). Берем начальное состояние q0 и вычисляем все состояния, в которые М переходит из q0 по символу а и по символу b:
q0a → q1, |
q0b→ q3, |
q0εa → q3, |
q0εb → q2, |
q0εa → q0, |
q0εb → q3, |
q0εaε → q2, |
q0εb → q1, |
т.е. θ'(q0, a) = {q0, q1, q2, q3} θ'(q0, b) = {q1, q2, q3}.
26 |
Конечные автоматы |
Теперь то же самое сделаем для q1:
q1a → q3, |
q1b→ q1, |
т.е. θ'(q1, a) = {q3}, θ'(q1, b) = {q1}. |
|
Далее для q2 : |
|
q2a → q0, |
q2b→ q3, |
q2aε → q2, |
q2b → q2, |
q2aε→ q1, |
|
т.е. θ'(q2, a) = {q0, q1, q2}, θ'(q2, b) = {q2, q3}.
Для q3 получаем:
q3a → q3, q3b→ q1,
т.е. θ'(q3, a) = {q3}, θ'(q3, b) = {q1}.
Наконец заметим, что q1 θ(q0, ε), т.е. ε допускается автоматом М, следовательно, q0 должно быть помещено в F'.
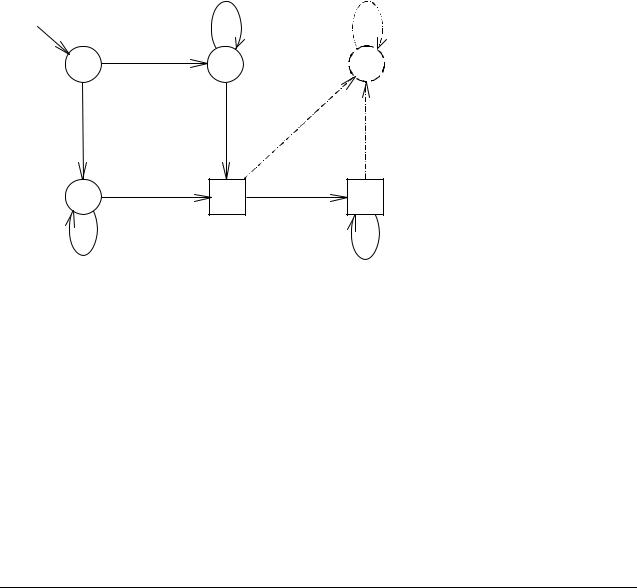
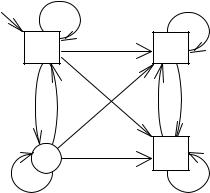
Таким образом, диаграмма DМ' автомата М' будет выглядеть следующим образом:
a |
|
|
|
q0 |
a, b |
q1 |
b |
b, a a |
b |
|
a |
a |
a,b |
|
|
q2 |
b |
q3 |
|
b,a |
|
|
a |
Нетрудно видеть, что если некоторая строка α L(M), то α
L(M'), и наоборот, т. е. L(M) = L(M').
Лекция 3 |
27 |
|
