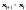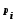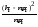4. Проверка согласия опытного распределения с теоретическим нормальным

Очень часто на практике, измеряемые численные параметры продукции, являющиеся случайными величинами, подчиняются нормальному закону распределения. Поэтому при планировании и проведении выборочного контроля по количественному признаку полагают, что контролируемый параметр имеет точно или приближенно нормальное распределение.

В случае отсутствии такой уверенности целесообразно осуществить проверку согласия опытного распределения контролируемого параметра с нормальным законом.

Требуется проверить гипотезу, что выборка взята из нормально распределенной генеральной совокупности при вероятности ошибки 0,05. Такая проверка будет проведена ниже с использованием одного из двух известных критериев согласия - критерия согласия Пирсона.[2]

Последовательность проверки гипотезы состоит в следующем:

1. Исследуется выборка из генеральной совокупности объемом 150 штук;

2. Используются данные из таблицы 3 для заполнения таблицы 5, причем разряды объединяются так, чтобы минимальная по величине разрядная часть была не меньше пяти (h_i ≥ 5);

3. Выдвигается нулевая гипотеза, что генеральная совокупность имеет нормальное распределение с функцией распределения 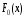и параметрами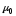и:;

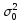4. Осуществляется проверка гипотезы на основе критерия, рассчитанного по формуле 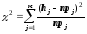(8):

, (8)

где 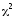- критерий согласия Пирсона;

k - количество интервалов интервального ряда;

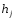- частота j-того интервала значений параметра х;

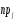- теоретическая частота j-того интервала значений х.

5. Находятся статистические характеристики выборк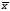и и.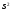

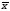= 49,1 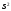=0,43 (по данным таблицы 4)

6. При расчете теоретических частот распределения учитывают, что 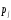есть вероятность того, что наблюдаемая случайная величинах генеральной совокупности попадает в j - тый интервал, т.е. х располагается между верхней (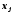) и нижней (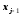) границамиj-того интервала.

7. В формуле (9) производится переход к нормированной случайной величине:

, (9)

где 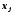- верхняя границаj-того интервала.

Тогда по формуле 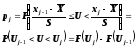(10):

, (10)

где 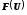– функция распределения нормированного нормального распределения случайной величиныU. При этом верхняя граница j-1 –ого интервала равна нижней границе j-того интервала.

8. Результаты расчетов приведены в таблице 5.

Таблица 5 – Расчет критерия согласия Пирсона.

Интервал	hi	Ui	F(Ui)			npi		½hi-npi½		(hi-npi)2
47,7-47,9	1	-1,85	0,032157	0,032157		9		1		1	0,111
47,9-48,1	7	-1,54	0,06178	0,029623
48,1-48,3	8	-1,23	0,109348	0,047568		7		1		1	0,142
48,3-48,5	14	-0,92	0,178786	0,069438		10		4		16	1,6
48,5-48,7	17	-0,61	0,270931	0,092145		13		4		16	1,23
48,7-48,9	16	-0,30	0,382088	0,111157		16		0		0	0
48,9-49,1	16	0	0,5	0,117912		17		1		1	0,058
49,1-49,3	2	0,30	0,617912	0,117912		48		31		961	20,02
49,3-49,5	1	0,61	0,729069	0,111157
49,5-49,7	14	0,92	0,821214	0,092145
49,7-49,9	37	1,23	0,888768	0,067554		10		27		729	72,9
49,9-50,1	17	1,54	0,938220	0,049452		7		10		100	14,285
Всего:					0,93822		137					110,346

Вычисление: U₁=

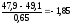
F(U₁)=1- F(-1,85)=1-0,967843=0,032157

P₂= F(U₂)- F(U₁)= 0,06178-0,032157=0,029623

np₁=(0,032157+0,029623)*150=9

½h₁-np₁½=½8-9½=1

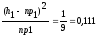
9. Т.к. 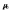и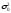неизвестны, то число степеней свободы будет рассчитываться по формуле (11): m = k-3. (11)

Вычисление: 9-3=6

10. Определяем критическое значение

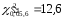
11. 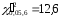<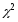= 110,346=> это свидетельствует о том, что гипотеза о нормальном распределении генеральной совокупности при выбранной вероятности ошибки отвергается.