
Архитектура учебник (book.pdf)
.pdfДомашнее задание по предмету: «Архитектура компьютеров».
Выполнила студентка 1 курса группы ИУ9-12 Юсупова Лилия.
2014 г.
Постановка задачи
Задача: разработать подпрограмму численного определения длины кривой, заданной в параметрическом виде и, по возможности, улучшить результаты ее работы.
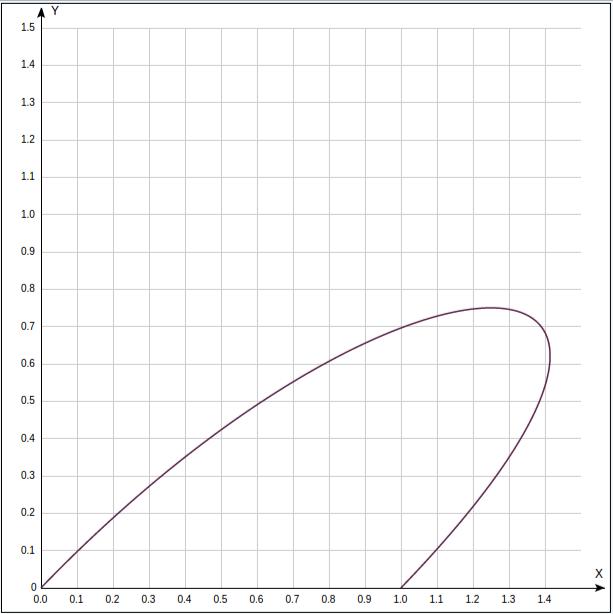
Тип кривой: плоская кривая Безье третьего порядка.
r=(1−t ) P0 +3 t (1−t) P1+3t |
(1−t )P2 |
+t |
P3 |
(Рисунок 1), |
|
|||||
|
3 |
|
2 |
2 |
|
|
3 |
|
|
|
r , P0 , P1 , P2 , P3 |
точки на плоскости и являются векторами (х,у). |
|||||||||
где |
||||||||||
|
|
|
P0=(0,0), |
P1=(1,1), P2=(2,1), |
P3=(1,0), t [0;1] . |
|||||
Начальные условия: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Для вычисления длины будем использовать формулу: |
|
|||||||||
L= |
r |
−r |
. |
|
|
|
|
|
|
|
|
∑i=1.. N−1 | i+1 |
i| |
|
|
|
|
|
|
|
|
Тип данных: float.
Рисунок 1: График кривой Безье
2
Наивная реализация
Рассмотрим наивную реализацию программы (Листинг 1).
Листинг 1. Наивная реализация.
#include <stdio.h> #include <math.h>
#define reference 2.48112398487 /* эталонное решение */
/* функция вычисления относительной погрешности */ float E (float rez) {
return (rez-reference)/(reference);
}
/* функция вычисления координат */
float F (float a0,float a1,float a2,float a3,float t) { float a;
a=pow((1-t),3)*a0+3*t*pow((1-t),2)*a1+3*t*t*(1-t)*a2+pow(t,3)*a3; return a;
}
/* функция вычисления длины через модуль разности векторов */ float Dl (float X, float x, float Y, float y) {
return (sqrt(pow((X-x),2)+pow((Y-y),2)));
}
/* функция вычисления длины кривой по координатам x,y */
float Dlina (int N,float x0,float y0,float x1,float y1,float x2,float y2,float x3,float y3) { float t,X,Y,x,y,l,L=0;
for (t=0;t<1;t+=(1.0/N)) { x=F(x0,x1,x2,x3,t); y=F(y0,y1,y2,y3,t); l=t+1.0/N; X=F(x0,x1,x2,x3,l); Y=F(y0,y1,y2,y3,l); L+=Dl(X,x,Y,y);
}
return L;
}
void main () {
float x0,y0,x1,y1,x2,y2,x3,y3,L,pogr; int N;
scanf("%f%f",&x0,&y0); /* считывание координат */ scanf("%f%f",&x1,&y1); /* считывание координат */ scanf("%f%f",&x2,&y2); /* считывание координат */ scanf("%f%f",&x3,&y3); /* считывание координат */ printf("Число шагов;Погрешность\n");
/* вывод таблицы для определения зависимости погрешности от кол-ва разбиений */ for (N=1;N<101;N++) { /* цикл для количества разбиений (1..100) */
L=Dlina(N,x0,y0,x1,y1,x2,y2,x3,y3); pogr=E(L); printf("%5d;%20.10f\n", N,pogr);
}
}
3

Построим график определения относительной погрешности для интервала |
|
||||||||||
t[0 ;1] . |
|
|
|
|
|
|
|
|
|
|
|
погрешность |
0,15 |
|
|
|
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|
|
|
Относительна |
-0,05 0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
-0,15 |
|
|
|
|
|
|
|
|
|
|
|
|
-0,25 |
|
|
|
|
|
|
|
|
|
|
|
-0,35 |
|
|
|
|
|
|
|
|
|
|
|
-0,45 |
|
|
|
|
|
|
|
|
|
|
|
-0,55 |
|
|
|
|
|
|
|
|
|
|
|
-0,65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число шагов |
|
Рисунок 2: График относительной погрешности для Листинга 1
По графику (Рисунок 2) видно, что при некоторых N (например, N=11) погрешность резко увеличивается.
Гипотеза №1.
Скорее всего так получается потому, что при данных значения N происходит лишняя итерация цикла.
Математическое обоснование:
Попробуем понять, почему же при вычислениях возникают и накапливаются погрешности. Главная причина кроется в устройстве типа float. По стандарту IEEE 754-2008 (включающий в себя стандарт IEEE 754-1985) ширина битового поля, выделенного под экспоненту типа float (равно, как и для типа double) ограничен (Рисунок 3), следовательно, при выполнении арифметических операций происходит округление и, соответственно, мы получаем неточный результат.
Рисунок 3: Представление числа с плавающей |
4 |
точкой [1] |
|
На Рисунке 3: S - бит знака (если S=0 – положительное число; S=1 – отрицательное число), E – смещенная экспонента двоичного числа, M – остаток мантиссы двоичного нормализованного числа с плавающей точкой.
Как следствие, получаем, что арифметические операции являются основной причиной возникновения ошибок.
Таким образом, любую арифметическую операцию с типом float можно представить как:
( A B)(1±e) , где e – погрешность операции.
Ожидаемый цикл:
tожид=(((t+dt)+dt)+dt+...+dt )
Полученный цикл:
tитог=((((t+dt )(1±e )+dt)(1±e)+dt)+...+dt )(1±e )
Понятно, что tожид≠tитог , так как e≠0 .
Проверим, так ли это на самом деле.
Настроим отладочную печать (Листинг 2) при N=10 и N=11.
Листинг 2. Настройка отладочной печати.
/* функция вычисления длины кривой по координатам x,y */
float Dlina (int N,float x0,float y0,float x1,float y1,float x2,float y2,float x3,float y3) { float t,X,Y,x,y,l,L=0;
int i=1;
for (t=0;t<1;t+=(1.0/N),i++) { /*добавлена новая переменная i для определения кол-ва шагов*/ x=F(x0,x1,x2,x3,t);
y=F(y0,y1,y2,y3,t); l=t+1.0/N; X=F(x0,x1,x2,x3,l); Y=F(y0,y1,y2,y3,l); L+=Dl(X,x,Y,y);
/*отладочная печать*/
printf("%2d %11.9f %11.9f %11.9f %11.9f %11.9f %11.9f \n", i,x,y,X,Y,t,L);
}
return L;
}
5
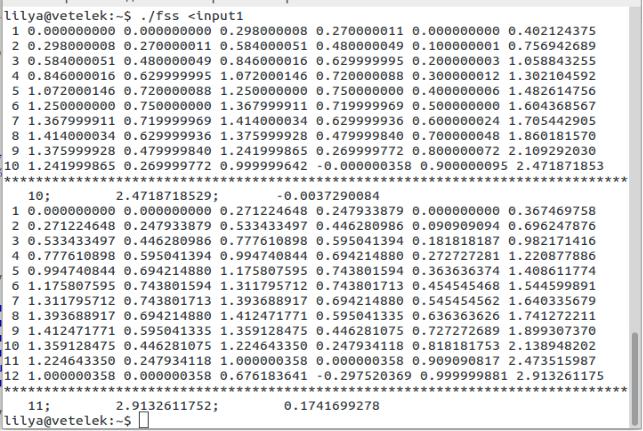
Рисунок 4: Отладочная печать для N=10 и N=11
Проанализируем полученный результат.
Как видим из иллюстрации, представленной выше (Рисунок 4), при N=10 программа разбивает кривую на 10 частей, а при N=11 (место «выброса») программа разбивает кривую на 12 частей, а не на 11, как должно быть. Так же, видим, что при N=11 на 11 шаге значение переменной L больше всего похоже на эталонное решение (2.48112398487) .
Возможное решение:
Попробуем решить эту проблему, установив счетчик шагов (Листинг 3).
6
Листинг 3. Изменение цикла на фиксированное количество шагов. |
|
|||||
/* функция вычисления длины кривой по координатам x,y */ |
|
|
|
|||
float Dlina (int N,float x0,float y0,float x1,float y1,float x2,float y2,float x3,float y3) { |
|
|||||
float t,X,Y,x,y,l,L=0; |
|
|
|
|
|
|
int i=0; /* начальное значение счетчика */ |
|
|
|
|||
for (t=0;t<1 && i<N;t+=(1.0/N),i++) { /* устанавливаем дополнительное условие */ |
|
|||||
|
x=F(x0,x1,x2,x3,t); |
|
/* выхода из цикла */ |
|
|
|
|
|
|
|
|
|
|
|
y=F(y0,y1,y2,y3,t); |
|
|
|
|
|
|
l=t+1.0/N; |
|
|
|
|
|
|
X=F(x0,x1,x2,x3,l); |
|
|
|
|
|
|
Y=F(y0,y1,y2,y3,l); |
|
|
|
|
|
} |
L+=Dl(X,x,Y,y); |
|
|
|
|
|
|
|
|
|
|
|
|
return L; |
|
|
|
|
|
|
} |
|
|
|
|
|
|
погрешность |
0,18 |
|
|
|
|
|
0,08 |
|
|
|
|
|
|
-0,02 0 |
|
|
|
|
|
|
Относительная |
20 |
40 |
60 |
80 |
100 |
|
-0,12 |
|
|
|
|
|
|
-0,22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,32 |
|
|
|
|
|
|
-0,42 |
|
|
|
|
|
|
-0,52 |
|
|
|
|
|
|
-0,62 |
|
|
|
Число шагов |
|
|
|
|
|
|
||
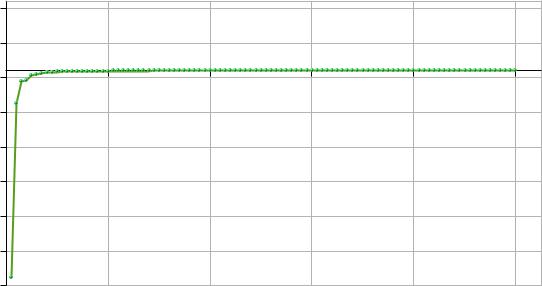
Рисунок 5: Относительная погрешность после установления счетчика
(Листинг 3)
Как можно заметить из графика (Рисунок 5), «выбросы» исчезли. Следовательно, наше решение было верным.
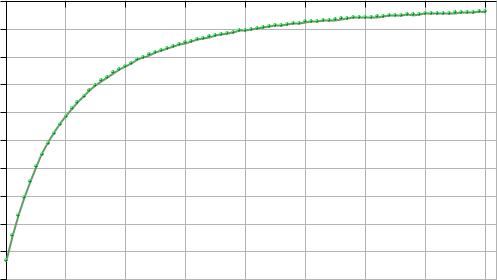
Для того, чтобы график вычисления относительной погрешности был нагляднее, построим его для N=20..100 (Рисунок 6).
7
погрешность |
0,00E+000 |
|
|
|
|
|
|
|
|
-1,00E-004 20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
-2,00E-004 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительная |
-3,00E-004 |
|
|
|
|
|
|
|
|
-4,00E-004 |
|
|
|
|
|
|
|
|
|
-5,00E-004 |
|
|
|
|
|
|
|
|
|
-6,00E-004 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-7,00E-004 |
|
|
|
|
|
|
|
|
|
-8,00E-004 |
|
|
|
|
|
|
|
|
|
-9,00E-004 |
|
|
|
|
|
|
|
|
|
-1,00E-003 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число шагов |
|
Рисунок 6: График относительной погрешности
Ограничив количество итераций цикла, мы, тем не менее, не избавились от погрешности вычисления t, а следовательно и не изменили точность
вычислений координат (x,y) вектора |
r . |
Гипотеза №2. |
|
На каждой итерации цикла результат вычисления переменной t суммируется с предыдущим, погрешность накапливается по принципу «снежного кома».
Математическое обоснование:
Каждое последующее слагаемое складывается с предыдущим, который, в свою очередь, уже был получен с погрешностью.
См. Математическое обоснование гипотезы 1, с 4.
Возможное решение:
Заменить суммирование умножением (Листинг 4), на i-том шаге , вместо i суммирований, мы получим всего 1 умножение.
8
Листинг 4. Замена суммирования умножением.
/* функция вычисления длины кривой по координатам x,y */
float Dlina (int N,float x0,float y0,float x1,float y1,float x2,float y2,float x3,float y3) { float t,X,Y,x,y,l,L=0;
int i=0;
for (;t<1 && i<N;i++ /* t+=1.0/N */) { /* убрали суммирование */ t=((float)i)/N; /* изменение переменной t */ x=F(x0,x1,x2,x3,t);
y=F(y0,y1,y2,y3,t);
l=((float)(i+1))/N; /* замена суммирования 2 */
X=F(x0,x1,x2,x3,l);
Y=F(y0,y1,y2,y3,l); L+=Dl(X,x,Y,y);
}
return L;
}
Теперь мы не накапливаем сумму при каждой итерации цикла, а вычисляем значение переменной t, пользуясь всего одной арифметической операцией.
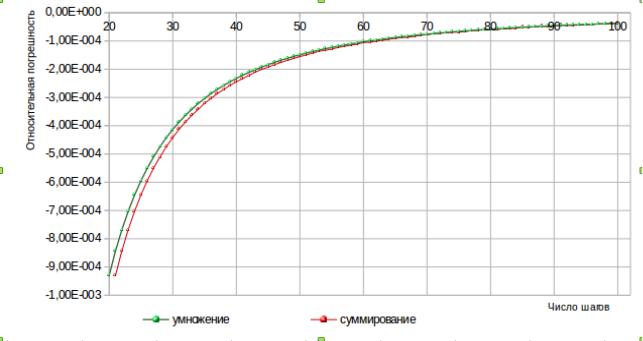
Рисунок 7: Относительная погрешность до и после изменения программы.
Оценим результат внесенных изменений. Судя по графикам (Рисунок 7), модуль относительной погрешности уменьшился. Следовательно, решение заменить суммирование умножением было правильным.
9
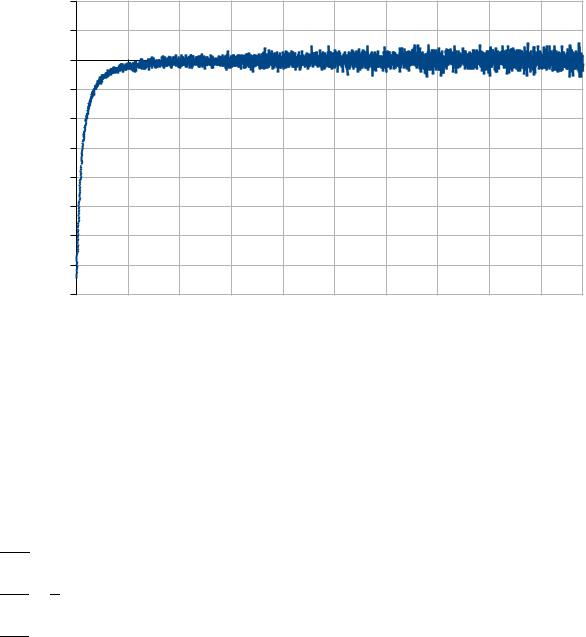
Мы знаем, как полученная программа работает (какую мы получаем |
||||||||||
погрешность) в диапазоне N=1..100. Проверим работоспособность программы |
||||||||||
для N=1..5000. |
|
|
|
|
|
|
|
|
|
|
Посмотрев на Рисунок 8 мы увидим, что при больших N в программе |
||||||||||
появляется все больше «скачков». |
|
|
|
|
|
|
||||
погрешност |
1,00E-005 |
|
|
|
|
|
|
|
|
|
5,00E-006 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительная |
0,00E+000 |
|
|
|
|
|
|
|
|
|
100 |
600 |
1100 |
1600 |
2100 |
2600 |
3100 |
3600 |
4100 |
4600 |
|
-5,00E-006 |
|
|
|
|
|
|
|
|
|
|
-1,00E-005 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1,50E-005 |
|
|
|
|
|
|
|
|
|
|
-2,00E-005 |
|
|
|
|
|
|
|
|
|
|
-2,50E-005 |
|
|
|
|
|
|
|
|
|
|
-3,00E-005 |
|
|
|
|
|
|
|
|
|
|
-3,50E-005 |
|
|
|
|
|
|
|
|
|
|
-4,00E-005 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число шагов |
Рисунок 8: Результаты работы программы при N=100..5000
Попробуем изменить начальные условия так, чтобы этот эффект («скачки») проявлялся при малых N. Подберем начальные условия такие, чтобы отношение длин минимального и максимального вектора при заданном разбиении было
равно некоторому коэффициенту k. Для этого закрепим три вектораP0 , P1 , P3 и найдем их длину:
P0=√0+0=0 ,
P1=√1+1=√2 ,
P3=√1+0=1 .
Вектор P2 оставим в виде коэффициента. Запишем полученную формулу для вычисления длины вектора r :
10
