
Архитектура учебник (book.pdf)
.pdf
r=3 √2(1−t)2+3t2 (1−t )P2 +t3 .
Знаем, что длина вектора тем больше, чем больше производная функции, задающей ее.
Найдем производную данной функции:
r '=3 √2(1−t)2−6 √2(1−t )+6 P2 t (1−t)−3 P2 t2+3t2=(9 √2−9 P2+3)t2−(12√2−6 P2 )t+3 √2 .
Найдем корни квадратного уравнения.
t1,2= |
6 √ |
2 |
−3±√ |
27−45 √ |
2 |
+27 √ |
2 |
P2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
9√2−9 P2+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Проанализировав |
производную |
|
можно |
понять, |
что максимальное значение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 √2−3−√27−45 |
√2+27 √ |
|
P2 |
|
|
|
|
|
|
||||||||||||
длины вектора |
r будет при |
t1 |
= |
2 |
, а минимальное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
9 √2−9 P2+3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 √ |
|
−3+√ |
|
|
|
|
|
|
|
|
|
||||||||
значение |
длины |
вектора будет |
при |
t2 = |
2 |
27−45 √ |
2 |
+27 √ |
2 |
P2 |
|
|
. Найдем |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
9 √2−9 P2 +3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
отношение |
|
, и, учитывая, что длина вектора |
|
r прямо пропорциональна |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
t3 |
, получим формулу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
t1 |
|
6 √ |
|
|
|
−3−√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
27−45 √ |
2 |
+27 √ |
2 |
P2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
=√k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
t2 |
6 √ |
|
−3+√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
27−45 √ |
|
+27 √ |
|
P2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Найдем |
P2 |
такое, что k=300. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Подставим в формулу k=300 и получаем, что длина вектора P2≈2102. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подберем такие значения x и y, чтобы длина вектора была равна 2102.
Пусть x=2100, y=2.5.
Проверим работоспособность программы при новых начальных условиях (Рисунок 9).
11
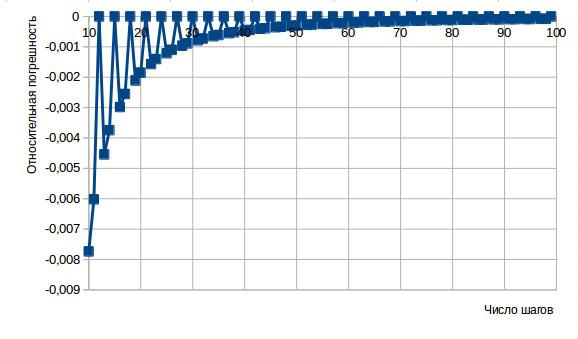
Рисунок 9: Относительная погрешность работы в "критических условиях"
Как видим, при новых начальных условиях «скачки» начали проявляться при малых N. Нас это не устраивает. Попробуем решить эту проблему.
Гипотеза №3.
Очевидно, что погрешность суммирования при вычислении длины L все также накапливается. Но избавится от нее путем замены одной арифметической операции на другую (как сделали в Листинге 4) не получится, так как длина каждого последующего полученного вектора, в любом случае, должна суммироваться с предыдущими результатами.
Математическое обоснование:
Вместо Lожид=(((L+dL)+dL)+dL+...+dL) ,
получаем, Lитог=((((L+dL)(1±e )+dL)(1±e)+dL)+...+dL)(1±e) .
Возможное решение:
Попробуем реализовать алгоритм Кэхэна (Листинг 5).
Википедия: «В вычислительной математике алгоритм Кэхэна — это алгоритм вычисления суммы последовательности чисел с плавающей запятой, который значительно уменьшает вычислительную погрешность по сравнению с наивным подходом. Уменьшение погрешности достигается введением
12
дополнительной переменной для хранения нарастающей суммы погрешностей» [2].
Листинг 5. Реализация функции нахождения длины с использованием алгорима Кэхэна.
/* функция вычисления длины кривой по координатам x,y */
float Dlina (int N,float x0,float y0,float x1,float y1,float x2,float y2,float x3,float y3) { float t,X,Y,x,y,l,L=0,pogr=0,true_l=0,TrueL=0; /* введение доп.переменных */ int i=1;
x=F(x0,x1,x2,x3,0); /* вычисление координат первого вектора */ y=F(y0,y1,y2,y3,0);
X=F(x0,x1,x2,x3,1.0/N);
Y=F(y0,y1,y2,y3,1.0/N); for (;t<1 && i<N;i++) {
true_l=Dl(X,x,Y,y)-pogr;
TrueL=L+true_l; /* L велика, true_l мало, так что младшие разряды true_l потеряны */ pogr=TrueL-L-true_l; /*восстановление разрядов pogr */
L=TrueL;
t=((float)i)/N; /* изменение переменной t */ x=F(x0,x1,x2,x3,t);
y=F(y0,y1,y2,y3,t); l=((float)(i+1))/N; X=F(x0,x1,x2,x3,l); Y=F(y0,y1,y2,y3,l);
true_l=Dl(X,x,Y,y)-pogr; L+=true_l;
return L;
}
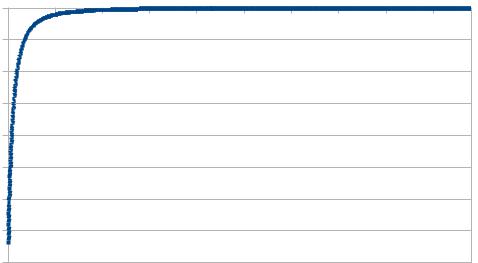
Оценим результат внесенных изменений для N=1000..5000 при начальных условиях (Рисунок 10).
Относительная погрешность
0,00E+000 |
|
|
|
|
|
|
|
|
|
100 |
600 |
1100 |
1600 |
2100 |
2600 |
3100 |
3600 |
4100 |
4600 |
-5,00E-006 |
|
|
|
|
|
|
|
|
|
-1,00E-005 |
|
|
|
|
|
|
|
|
|
-1,50E-005 |
|
|
|
|
|
|
|
|
|
-2,00E-005 |
|
|
|
|
|
|
|
|
|
-2,50E-005 |
|
|
|
|
|
|
|
|
|
-3,00E-005 |
|
|
|
|
|
|
|
|
|
-3,50E-005 |
|
|
|
|
|
|
|
|
|
-4,00E-005 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число шагов |
|
Рисунок 10: Результат работ программы с алгоритмом Кэхэна
при начальных условиях. |
13 |
|
Как видим из графика результат работы программы с реализацией алгоритма Кэхэна (Рисунок 10 ) для Листинга 5, «скачки» исчезли.
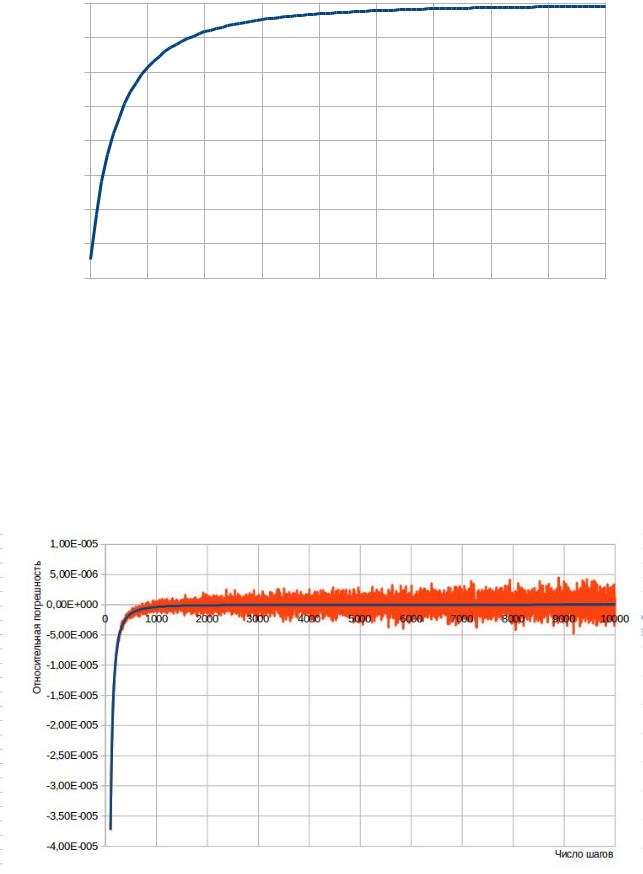
Теперь посмотрим результат работы программы с реализацией алгоритма Кэхэна в критических условиях при N=1000..5000 (Рисунок 11).
погрешность |
0 |
|
|
|
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Относительная |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число шагов |
|
|
|
Рисунок 11: График работы программы в критических условиях
Как можно заметить, «скачки» при работе прог ≈−1,5 10−6 раммы исчезли. Реализация алгоритма Кэхэна значительно улучшила результаты работы программы (Рисунок 9 и 11). Построим графики для Листинга 4 и Листинга 5 в одной области для их сравнения и анализа.
Рисунок 12: Листинг 4 и 5. N=1..10000
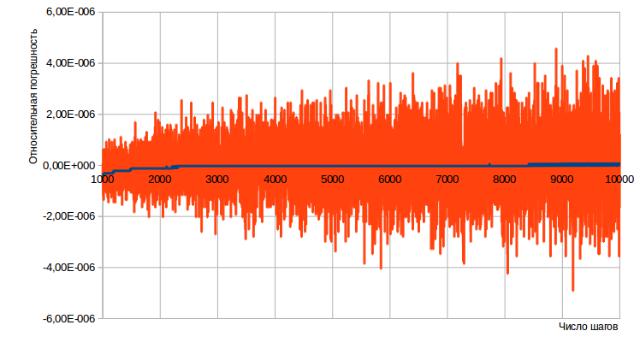
Рисунок 13: Листинг 4 и 5. N=1000..10000
Из Рисунок 12 можно заметить, что при N ~ 1..500 графики Листинга 4 и Листинга 5 совпадают. Это означает, что при малом числе шагов реализация алгоритм Кэхэна незначительно повлияла на погрешность вычислений, что же происходит при больших N?
Рассмотрим график относительной погрешности для листингов 4 и 5 для N=1000..10000 (Рисунок 13). Как видим, для больших N алгоритм Кэхэна существенно влияет на вычисление длины. Можно заметить, что при реализации функции вычисления длины кривой без алгоритма Кэхэна наблюдаются большое количество «скачков» в графике относительной погрешности (как в положительную, так и в отрицательную сторону). При реализации же данного алгоритма мы получаем плавно изменяющийся график относительной погрешности, причем ЕЛистинг 5→0 , а также ЕЛистинг 4 ЕЛистинг 5 .
Это означает, что высказанная гипотеза верна. Реализация алгоритма Кэхэна в функции вычисления длины значительно улучшила программу, уменьшив погрешность вычислений.
15
Листинг 6. Итоговая программа.
#include <stdio.h> #include <math.h>
#define reference 2.48112398487 /* эталонное решение */
/* функция вычисления относительной погрешности */ float E (float rez) {
return (rez-reference)/(reference);
}
/* функция вычисления координат */
float F (float a0,float a1,float a2,float a3,float t) { float a;
a=pow((1-t),3)*a0+3*t*pow((1-t),2)*a1+3*t*t*(1-t)*a2+pow(t,3)*a3; return a;
}
/* функция вычисления длины через модуль разности векторов */ float Dl (float X, float x, float Y, float y) {
return (sqrt(pow((X-x),2)+pow((Y-y),2)));
}
/* функция вычисления длины кривой по координатам x,y */
float Dlina (int N,float x0,float y0,float x1,float y1,float x2,float y2,float x3,float y3) { float t,X,Y,x,y,l,L=0,pogr=0,true_l=0,TrueL=0;
int i=1; x=F(x0,x1,x2,x3,0); y=F(y0,y1,y2,y3,0); X=F(x0,x1,x2,x3,1.0/N); Y=F(y0,y1,y2,y3,1.0/N); for (;t<1 && i<N;i++) {
true_l=Dl(X,x,Y,y)-pogr; TrueL=L+true_l; pogr=TrueL-L-true_l; L=TrueL;
t=((float)i)/N; x=F(x0,x1,x2,x3,t); y=F(y0,y1,y2,y3,t); l=((float)(i+1))/N; X=F(x0,x1,x2,x3,l); Y=F(y0,y1,y2,y3,l);
}
true_l=Dl(X,x,Y,y)-pogr; L+=true_l;
return L;
}
void main () {
float x0,y0,x1,y1,x2,y2,x3,y3,L,pogr; int N;
scanf("%f%f",&x0,&y0); /* считывание координат */ scanf("%f%f",&x1,&y1); /* считывание координат */ scanf("%f%f",&x2,&y2); /* считывание координат */ scanf("%f%f",&x3,&y3); /* считывание координат */ printf("Число шагов;Погрешность\n");
for (N=1000;N<5001;N++) { /* цикл для количества разбиений (1..100) */
L=Dlina(N,x0,y0,x1,y1,x2,y2,x3,y3); pogr=E(L); printf("%5d;%20.10f\n", N,pogr);
}
}
16
Список литературы.
[1]IEEE 754 — Стандарт двоичной арифметики с плавающей точкой [электронный ресурс] .- Доступ к ресурсу: http://www.softelectro.ru/ieee754.html .
[2]Алгоритм Кэхэна [электронный ресурс] .- Доступ к ресурсу:
https://ru.wikipedia.org/wiki/Алгоритм_Кэхэна .
17
