
barsukov-a
.pdf
6. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И УРАВНЕНИЯ МАКСВЕЛЛА
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
6.1. СОБСТВЕННЫЕ НЕЗАТУХАЮЩИЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
1.Периодические колебания величин, характеризующих электрические и магнитные поля, называются электромагнитными колебаниями.
2.Различают колебания полей, связанных с зарядами и токами, и колебания полей, существующих
вотрыве от зарядов и токов. Первые имеют место в электрических цепях, вторые – в электромагнитных волнах.
3.Электрическая цепь, в которой могут происходить электромагнитные колебания, называется колебательным контуром.
Колебательным контуром может служить любая цепь, даже простой отрезок провода; необходимо только определённое соотношение между электроёмкостью, индуктивностью и сопротивлением цепи (R, L, C – свойства, присущие любой цепи, любому проводнику).
4.Если электрическое и магнитное поля в колебательном контуре пространственно разобщены и локализованы в сравнительно небольших областях, контур называется закрытым (контур с сосредоточенными параметрами). В противном случае контур называется открытым (контур с распределёнными параметрами).
5.Простейший закрытый колебательный контур – это соединенные между собой конденсатор и катушка индуктивности. Хотя катушка обладает некоторой ёмкостью, а конденсатор – индуктивностью, будем полагать, что ёмкость сосредоточена только в конденсаторе, индуктивность – только в катушке и, кроме того, омическое сопротивление контура равно нулю (такой закрытый контур называется идеальным).
6.Чтобы в контуре возникли электромагнитные колебания контур необходимо вывести из состояния равновесия. Для этого достаточно зарядить конден-
С |
L |
сатор (или возбудить ток в катушке) и предоставить контур самому себе. При- |
|
соединим конденсатор к источнику постоянного напряжения (рис. 6.1).
В процессе зарядки обкладки конденсатора приобретут разноимённые заряды
±q0 , в результате чего в конденсаторе возникнет электрическое поле с энергией
Рис. 6.1
WE = q02 ,
2C
где C – ёмкость конденсатора.
7. Переключим конденсатор на катушку. Концы катушки приобретут потенциалы обкладок, внутри провода катушки возникнет электростатическое поле. Это поле приведёт в направленное движение свободные заряды катушки. Начнётся нейтрализация зарядов на обкладках конденсатора – разрядка конденсатора. Разрядный ток будет нарастать, но постепенно вследствие самоиндукции: ЭДС самоиндукции будет препятствовать мгновенному нарастанию тока. Напряжение, приложенное к катушке, ускоряет носители тока, ЭДС самоиндукции, напротив, тормозит их.
На рисунке 6.2, а изображена часть витка катушки. Ток течёт в сторону убыли потенциала. В этом направлении действуют на положительные заряды силы электростатического поля. Виток пронизывается нарастающим магнитным полем (ток в катушке растёт). Изменяющееся магнитное поле создаст в катушке и за её пределами вихревое электрическое поле. Силы этого поля вызовут в витке ток самоиндукции такого направления, что магнитное поле этого тока будет препятствовать нарастанию магнитного потока пронизывающего виток. Чтобы магнитное поле тока самоиндукции было противоположно магнитному полю тока в катушке, необходимо, чтобы линии вихревого электрического поля были направлены так, как это показано на рисунке (это направление соответствует направлению тока самоиндукции).
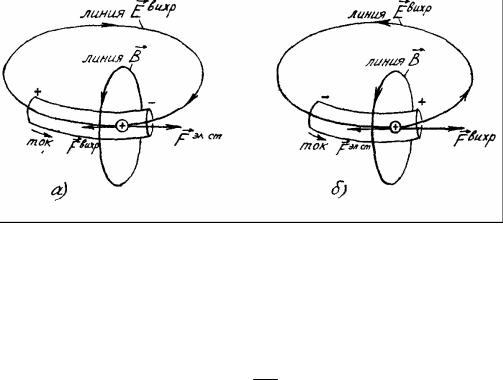
Рис. 6.2
8. В процессе разрядки конденсатора разность потенциалов на обкладках, заряд обкладок, напряжённость электрического поля уменьшаются, соответствующие характеристики магнитного поля возрастают. Энергия электрического поля конденсатора постепенно превращается в энергию магнитного поля катушки. В момент, когда конденсатор полностью разрядится, энергия электрического поля будет равна нулю, а энергия магнитного поля максимальна
LI 2
W = 0 ,
B |
2 |
|
где L – индуктивность катушки; I0 – максимальный ток в катушке.
Этим мгновением заканчивается первая стадия колебательного процесса.
9. Если бы контур не был разорван обкладками конденсатора, то ток I0 существовал бы в нём сколь
угодно долго, не нуждаясь ни в напряжении, ни в ЭДС: ведь сопротивление контура равно нулю (в момент, когда ток в контуре достигает максимального значения I0 , и напряжение, и ЭДС самоиндукции
равны нулю). Наличие в контуре конденсатора приводит к тому, что ток на его обкладках обрывается,
заряды здесь тормозятся и накапливаются: на той обкладке, по направлению к которой течёт ток, нака-
.
пливаются положительные заряды, на другой обкладке – отрицательные. Это приводит к тому, что в
конденсаторе и в катушке вновь возникает электростатическое поле, но теперь уже противоположного направления. Это поле тормозит движение зарядов катушки. Ток, а следовательно, и его магнитное поле начинают убывать. Уменьшение магнитного поля сопровождается возникновением ЭДС самоиндукции, возникновением вихревого электрического поля, которые препятствуют уменьшению тока и поддерживают его первоначальное направление (проанализируйте рис. 6.2, б). Благодаря совместному действию вихревого и кулоновского полей ток постепенно уменьшается до нуля. Энергия магнитного поля снова переходит в энергию электрического поля. Этим завершается вторая стадия цикла.
На третьей и четвертой стадиях повторятся те же процессы, что и на первой и второй стадиях, но в обратном направлении. Пройдя все эти четыре стадии, контур вернётся в исходное состояние. Последующие циклы будут в точности повторяться.
Таким образом, в колебательном контуре периодически изменяются (колеблются) следующие фи-
зические величины: q – заряд на обкладках конденсатора; U – |
разность потенциалов на конденсаторе и, |
||
R |
|
R |
ин- |
следовательно, на концах катушки; i – ток в катушке; Е – |
напряжённость электрического поля; В – |
||
дукция магнитного поля; WE – энергия электрического поля; WB – энергия магнитного поля.
10. Сопоставляя электромагнитные колебания с механическими, например, с колебаниями пружинного маятника, нетрудно подметить, что каждой величине, характеризующей механические колебания, соответствует электрическая или магнитная величина, играющая в электромагнитных колебаниях ана-
логичную роль. Так, координате x соответствует заряд q, |
скорости υ – ток i, потенциальной энергии |
|||
|
|
|
|
R |
пружины |
kx2 |
– энергия электрического поля конденсатора |
q2 |
, и т.д. |
|
2C |
|||
2 |
|
|
||
Приводим список таких величин.
Механические |
|
|
|
Электромагнитные |
|
|
|
|
колебания |
|
|
|
колебания |
|
|
|
|
Инерция |
|
|
|
Самоиндукция |
|
|
|
|
Масса |
|
m |
Индуктивность |
|
L |
|||
Коэффициент |
|
k |
Величина, обратная |
|
1 |
|
||
упругости |
|
ёмкости |
|
C |
||||
|
|
|
|
|||||
Координата |
|
x |
Заряд конденсатора |
|
q |
|||
Скорость |
|
u |
Ток |
|
i |
|||
|
|
R |
|
|
|
|
|
|
Потенциальная |
|
kx2 |
|
Энергия электриче- |
q2 |
|||
энергия |
2 |
|
ского поля |
2C |
||||
Кинетическая |
mu2 |
Энергия магнитного |
Li2 |
|||||
энергия |
2 |
|
поля |
|
2 |
|
||
Коэффициент |
|
r |
Омическое сопротив- |
|
R |
|||
трения |
|
ление |
|
|||||
|
|
|
|
|
|
|||
Внешняя сила |
|
R |
Электродвижущая си- |
|
ε |
|||
|
F |
ла |
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
Напряжение |
|
U |
||
11. Найдём вид зависимости от времени колеблющихся физических величин. Будем полагать, что процессы в контуре происходят достаточно медленно: мгновенные значения тока одинаковы во всех сечениях контура и, следовательно, к контуру применимы законы постоянного тока.
Чтобы найти закон изменения данной переменной величины, нужно составить для неё дифференциальное уравнение и найти решение этого уравнения.
Начнём c заряда конденсатора. Так как контур не излучает волн и не выделяет тепла, его энергия,
складывающаяся из энергии магнитного поля
менной
где I и q – мгновенные значения тока и заряда. Продифференцируем (6.1.1) по времени
Li2 |
и энергии электрического поля |
q 2 |
|||||
2 |
2C |
||||||
|
|
|
|
|
|||
|
|
Li2 |
+ |
q 2 |
= const , |
||
|
2 |
2C |
|||||
|
|
|
|
||||
, остаётся неиз-
(6.1.1)
Li |
di |
+ |
q |
|
dq |
= 0. |
(6.1.2) |
|
|
|
|||||
|
dt C dt |
|
|||||
Мы полагаем, что среда, в которой находится контур, неферромагнитная, и, следовательно, L ¹ L(i). Производные по времени будем обозначать точкой над дифференцируемой величиной:
|
|
|
|
|
dq |
= q , |
|
di |
= i . |
|
|
|
||
|
|
|
|
|
|
|
& |
|
|
& |
|
|
|
|
|
|
|
|
|
dt |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Учтём, что i = |
dq |
= q , |
i = q . Разделим обе части уравнения (6.1.2) на |
Li и воспользуемся введёнными |
||||||||||
|
dt |
& |
& |
&& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначениями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
&& |
+ |
1 |
q = 0. |
|
|
|
||||
|
|
|
|
|
q |
LC |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначив |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= w02 , |
(6.1.3) |
|
|
|
|
|
|
|
|
|
|
|
|
LC |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим искомое дифференциальное уравнение для заряда |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 0 . |
(6.1.4) |
|
|
|
|
|
|
|
|
|
|
|
q + w0 q |
|||
|
|
|
|
|
|
|
|
|
|
&& |
|
|
|
|

Решение этого уравнения имеет вид |
|
q = qm cos(w0t + j0 ), |
(6.1.5) |
где qm – амплитудное значение заряда; j0 – начальная фаза; ω0 – циклическая частота колебаний.
Как видно из (6.1.5), заряд на обкладках конденсатора изменяется по гармоническому закону. Частота ω0 называется собственной. Период собственных колебаний контура равен
|
|
|
|
|
|
T = |
2p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
w0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив в эту формулу выражение для ω0 по (6.1.3), получим формулу Томсона |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T = 2p |
|
|
. |
|
|
|
|
|
|
|
|
(6.1.6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
LC |
|
|
|
|
|
|
|
|
||||||||
Частота собственных колебаний равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n = |
1 |
= |
|
1 |
|
. |
|
|
|
|
|
|
(6.1.7) |
||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2p LC |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Разделив уравнение (6.1.5) на C, найдём закон изменения напряжения на конденсаторе |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
U = U m cos (w0t + j0 ), |
|
|
|
|
|
|
(6.1.8) |
|||||||||||
где U m |
= |
qm |
– |
амплитуда напряжения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закон изменения тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
+ j0 ) |
|
|
|
|
p |
(6.1.9) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= I m cos w0t + j0 + |
|
|
, |
||||||||||
|
|
|
|
|
|
|
i = q = -w0qm sin(w0t |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
где Im = w0qm – |
амплитуда тока. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Закон изменения ЭДС самоиндукции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
es = -Li& = Lw02qm cos (w0t + j0 )= esm cos (w0t + j0 ), |
(6.1.10) |
|||||||||||||||||||||
где e |
sm |
= Lw2q |
m |
– амплитуда ЭДС самоиндукции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Закон изменения энергии электрического поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
W = |
q 2 |
= |
qm2 |
cos |
2 (ω |
t + ϕ |
0 |
|
)= W |
cos 2 (ω |
t + ϕ |
0 |
), |
(6.1.11) |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
E |
|
2C |
|
2C |
|
|
0 |
|
|
|
|
Em |
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где WEm = qm2 – амплитуда энергии электрического поля.
2C
Закон изменения энергии магнитного поля
|
|
|
W = |
Li2 |
= |
Lω02 qm2 |
sin |
2 (ω |
t + ϕ |
0 |
)= W |
sin |
2 (ω |
t + ϕ |
0 |
), (6.1.12) |
|
|
|
|
|||||||||||||
|
|
|
B |
2 |
|
2 |
|
0 |
|
Bm |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где W = |
Lω2 q |
2 |
– амплитуда энергии магнитного поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Bm |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ввыражения для амплитуд всех изменяющихся величин входит амплитуда заряда qm. Эта величина,
атакже начальная фаза колебаний j0 определяются начальными условиями – зарядом конденсатора и
током в контуре в начальный момент времени t = 0. Если отсчёт времени вести с момента замыкания контура, то при t = 0, q = q0 и i = 0. Подставив эти значения в уравнения (6.1.5) и (6.1.9), получим:
q0 = qm cos j0 ;
0 = -w0qm sin j0 .
Из второго уравнения получаем j0 = 0.
Подставив j0 = 0 в первое уравнение, найдём, что qm = q0 , т.е. амплитуда заряда равна первоначальному заряду конденсатора. Если время отсчитывать от другого мгновения, связь между qm и q0 будет иной и j0 ¹ 0 .
Сопоставляя (6.1.5), (6.1.8) – (6.1.12), заключаем, что колебания заряда, напряжения, ЭДС самоиндукции совершаются в одинаковых фазах. Ток опережает по фазе эти величины на π/2. Частота колебаний энергии электрического и магнитного полей в два раза больше частоты колебаний всех других величин.
Графики всех этих величин изображены на рис. 6.3.
q

t
u
t
i
t
εs
t
WЕ
t
WВ
t
Рис. 6.3
6.2. СОБСТВЕННЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Любой реальный контур обладает омическим сопротивлением.
В реальном контуре электромагнитная энергия, запасённая в начале колебаний, постепенно превращается в тепло. Колебания вследствие этого затухают.
Составим дифференциальное уравнение собственных затухающих колебаний. Из закона изменения энергии следует, что убыль энергии электрического и магнитного полей контура за время dt равна количеству выделившегося в контуре тепла:
|
Li2 |
|
q 2 |
|
|
|
− d |
|
+ |
|
|
= i 2 Rdt . |
(6.2.1) |
|
|
|||||
|
2 |
|
|
|
|
|
|
|
2C |
|
|
||
Найдём дифференциал величины, стоящей в скобках, и разделим обе части уравнения на dt. Полу-
чим
− Lii& − qq& = i2 R. C
Перенесем i2R в левую часть, умножим обе части уравнения на (–1) и разделим все слагаемые на Li:
|
|
|
|
|
|
|
i& + |
R |
i + |
1 |
q = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
L |
LC |
|
|
|
|||
Обозначим i = q , i = q , |
R |
= 2β , |
1 |
= ω0 . |
|
|
|
|
|
||||||
& |
&& |
& |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
L |
|
LC |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получим искомое дифференциальное уравнение: |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q + |
|
2 |
(6.2.2) |
|
|
|
|
|
|
|
|
|
|
|
|
2βq + ω0 q = 0 . |
|||
|
|
|
|
|
|
|
|
|
|
|
&& |
& |
|
|
|
Решение этого уравнения при β < ω0 имеет вид |
|
q = qm0 e-b×t cos(ωt + ϕ0 ), |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(6.2.3) |
|||
где qm0 – начальная амплитуда заряда; ω = |
|
– |
|
|
|||||||||||
ω02 − β2 |
циклическая частота колебаний. |
|
|||||||||||||
3. Как видно из (6.2.3), собственные затухающие колебания не являются гармоническими: амплитуда таких колебаний с течением времени уменьшается по закону: A = qm0 e-b×t . Показатель β называется коэффициентом затухания. График q = q(t) собственных затухающих колебаний изображен на рис. 6.4.
|
q |
qm0 |
q = qm0е– βt |
0
t
q = –q m0е– βt
–q m0
Рис. 6.4
4. Разделив (6.2.3) на С, найдём закон изменения напряжения

U = U m0e-bt cos (ωt + ϕ0 ), |
(6.2.4) |
где Um0 – амплитуда заряда в начальный момент времени.
5. Чтобы найти закон изменения тока, продифференцируем (6.2.3) по времени
|
|
|
i = q = qm0e |
-bt |
[− β cos(ωt + ϕ0 ) − ωsin(ωt + ϕ0 )]. |
(6.2.5) |
|||
|
|
|
|
& |
|
|
|
|
|
Умножим и разделим правую часть этого выражения на ω0: |
|
|
|||||||
i = ω q |
e-bt − |
β |
cos(ωt + ϕ )− |
ω |
sin(ωt + ϕ ) . |
|
|||
ω0 |
|
|
|||||||
0 m0 |
|
0 |
|
ω0 |
|
|
|
||
|
|
|
|
|
|
0 |
|
||
Введём величину ψ, удовлетворяющую условиям
cos ψ = − |
β |
, |
sin ψ = |
ω |
. |
ω |
|
||||
|
|
|
ω |
||
|
0 |
|
|
0 |
|
Обозначим также ω0qm0 = Im0 . Тогда выражение для тока приобретет вид i = Im0e-bt [cos ψ cos(ωt + ϕ0 )− sin ψ sin(ωt + ϕ0 )].
Воспользовавшись известной тригонометрической формулой сложения, получим
i = Im0e-b×t cos(ωt + ϕ0 + ψ) . |
(6.2.6) |
Так как cosψ < 0, а sin ψ > 0, то π < ψ < π . 2
Величина ψ – определяет фазовый сдвиг между током и напряжением: ток в катушке индуктивности опережает по фазе напряжение на конденсаторе более чем на π/2.
6. Циклическая частота затухающих колебаний меньше собственной частоты контура: ω < ω0. Условный период затухающих колебаний равен
T = |
2π |
= |
|
|
2π |
|
|
= |
|
|
2π |
|
|
. |
(6.2.7) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ω |
|
ω0 − β |
2 |
|
1 |
|
|
R |
2 |
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4L2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
LC |
|
|||||
7. Отношение двух последующих амплитуд называется декрементом затухания |
|
|||||||||||||||||
|
|
|
A |
|
= |
|
q |
e-bt |
|
= ebT . |
(6.2.8) |
|||||||
|
|
|
|
t |
|
|
0 |
|
|
|
|
|||||||
|
|
|
A |
|
q e-b(t +T ) |
|
||||||||||||
|
|
|
|
t +T |
|
0 |
|
|
|
|
|
|
|
|
|
|
||
8. Логарифм отношения двух последующих амплитуд называется логарифмическим декрементом затухания
|
|
|
|
|
|
|
|
|
|
|
|
|
qm0e-b×t |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
λ = ln |
qm0e |
-b(t +T ) |
= βT . |
(6.2.9) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. Время релаксации затухающих колебаний τ – |
время, |
в течение которого амплитуда колебаний |
|||||||||||||||||
уменьшается в е раз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
qm0e-b×t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из условия |
qm0e |
-b(t +t) |
= e находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = |
1 |
|
и |
|
|
|
β = |
1 |
. |
(6.2.10) |
|||
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
τ |
|
|||
Таким образом, |
коэффициент затухания – это величина, |
обратная времени, в течение которого ам- |
|||||||||||||||||
плитуда колебаний уменьшается в е раз. |
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|||||
10. Подставим выражение для β в (6.2.8): λ = |
T |
. Но |
= N – число колебаний, совершаемых за время |
||||||||||||||||
τ |
|
||||||||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
||||
релаксации. Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
λ = |
1 |
. |
(6.2.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
N |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, логарифмический декремент затухания – |
величина, обратная числу колебаний, со- |
||||||||||||||||||
вершаемых за время релаксации.
11. Для характеристики затухания колебаний вводят также добротность Q, связанную с логарифми-
ческим декрементом соотношением |
π |
|
|
Q = |
(6.2.12) |
||
λ |
|||
|
|
Такой заряд конденсатор получает при подключении его к источнику с постоянной ЭДС εm .
При Ω → ∞ qm → 0.
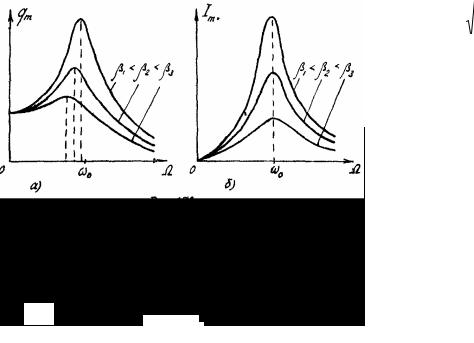
Высота резонансного пика и его «острота» тем больше, чем меньше β, т.е. чем меньше омическое сопротивление и больше индуктивность контура. Резонансные кривые для qm , соответствующие разным β, приведены на рис. 6.6, а.
Резонансную частоту для тока легко найти из (6.3.13): амплитуда тока |
максимальна |
при |
|||||
1 |
− ΩрезL = 0 , откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ΩрезC |
|
|
|
|
|
|
|
|
Ωрез,i = |
|
1 |
|
= ω0 . |
(6.3.16) |
|
|
|
|
|||||
|
|
|
LC |
|
|
||
Резонансная частота для тока совпадает с собственной частотой |
контура. При Ω → 0 i → 0; |
при |
|||||
Ω → ∞ i → 0 . |
|
|
|
|
|
|
|
Первое означает, что при постоянной ЭДС установившийся ток в цепи с конденсатором течь не может. Резонансные кривые для амплитуды тока приведены на рис. 6.6, б.
|
|
|
|
qm |
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
Из формул (6.3.1), (6.3.4) – (6.3.6) |
вид- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но, что колебания заряда, напряжения и |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тока сдвинуты по фазе относительно ЭДС. |
||||
|
|
|
|
|
|
|
|
β1 < β2 < β3 |
|
|
|
|
|
|
|
|
β1 < β2 |
< β3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот сдвиг тем больше, |
чем больше R и чем |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньше разность ΩL − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ΩC |
|
||
εC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Явление резонанса |
|
используется |
для |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выделения из сложного напряжения нужной |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составляющей. Пусть, например, к контуру |
||||
|
0 |
|
|
|
|
ω0 |
|
|
Ω |
0 |
|
|
|
|
|
ω0 |
|
|
Ω |
||||||||
|
|
|
а) |
|
|
|
|
б) |
|
|
|
|
приложено напряжение |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.6 |
U =U m1 cos (Ω1t + α01 )+U m2 cos (Ω2t + α02 ). |
|
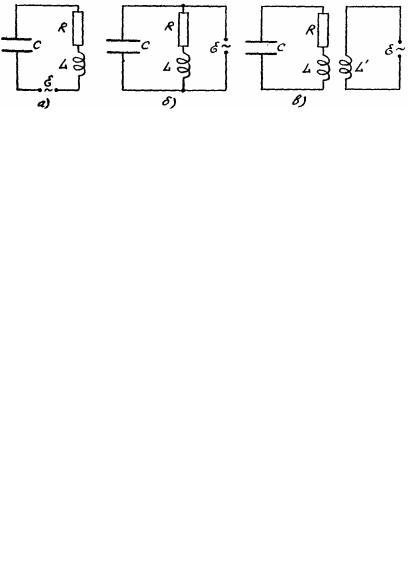
Настроив контур в резонанс с одной из частот, можно получить на конденсаторе напряжение, значительно превышающее величину данной составляющей, в то время как напряжение, создаваемое другими составляющими, будет мало. Такой процесс осуществляется, например, при настройке радиоприёмника на нужную длину волны.
УРАВНЕНИЯ МАКСВЕЛЛА
Между электрическими зарядами и токами, с одной стороны, и создаваемыми ими электрическими
имагнитными полями, с другой, существует связь. Связь существует и между самими электрическими
имагнитными полями. Эта связь проявляется в том, что электрическое и магнитное поля способны порождать друг друга. При всяком изменении магнитного поля возникает электрическое поле и, наоборот, при всяком изменении электрического поля возникает магнитное поле. Уравнения Максвелла в сжатой математической форме отражают все эти связи и все эти процессы.
6.4.ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛА
1. Следуя Максвеллу, обобщим явление электромагнитной индукции.
Как известно, при изменении магнитного потока, пронизывающего неподвижный проводящий контур, в последнем возникает вихревое электрическое поле, которое и создаёт ЭДС индукции.
Максвелл установил, что проводящий контур в этом процессе не играет принципиальной роли, а является лишь прибором, обнаруживающим вихревое электрическое поле. Переменное магнитное поле создает вихревое электрическое поле независимо от того, имеются или нет проводники в той области пространства, где существует переменное магнитное поле.
Таким образом, переменное магнитное поле порождает вихревое электрическое поле.
2. Придадим выражению закона электромагнитной индукции
εi |
= − |
dФ |
. |
(6.4.1) |
|
||||
|
|
dt |
|
|

