barsukov-a

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тамбовский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

×80 ×(0,1)2

= 6,28 ×10−5

.pdf

Скачиваний:

Добавлен:

22.05.2015

Размер:

5.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1511 12 13 14 15 > Следующая >>>

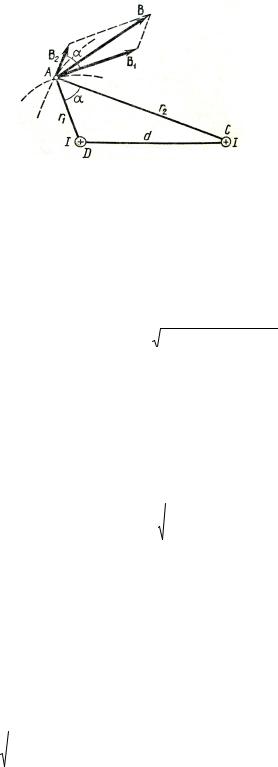
Рис. 3.30

Решение. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций В1 и В2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:

B = B1 + B2 .

Модуль вектора В может быть найден по теореме косинусов:

B =

+ B2

+ 2B B cos a ,

(1)

где a – угол между векторами В1

и В2 .

Магнитные индукции В1 и В2

выражаются соответственно через силу тока I и расстояния r1

и r2 от

поводов до точки А:

m0 I

;

m0 I

2pr1

2pr2

Подставляя выражения В и В

в формулу (1) и вынося m0 I

за знак корня, получаем

B = m0I

cos a .

(2)

r 2

r r

1 2

Вычислим cosa. Заметив, что a = Ð DAC (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем

d 2 = r12 + r22 - 2r1r2 cos a ,

где d – расстояние между проводами. Отсюда

	r 2	+ r 2	- d	2	; cos a =	52 +122 -102		23	.
cos a =	1	2					=
cos a =		2r1r2				2 ×5 ×12	=	40
		2r1r2				2 ×5 ×12		40

Подставив в формулу (2) числовые значения физических величин и произведём вычисления:

	4 ×3,14 ×10−7 ×60
B =			1	+	1		2	23	= 3,08 ×10−4 =
		(0,05)2			(0,12)2	0,05 ×0,12 40
2 ×3,14

= 308 мкТл.

Пример 2. По тонкому проводящему кольцу радиусом R = 10 см течёт ток I = 80 А. Найти магнит-

ную индукцию B в точке А, равноудалённой от всех точек кольца на расстояние r = 20 см. Решение. Для решения задачи воспользуемся законом Био– Савара– Лапласа:

	R		RR
	R		[Idl r ]
	dB =	m0	[Idl r ]	,
	dB =	4p	r 3	,
		4p	r 3
где	R				R	в точке, определяемой радиусом-
где	dB – магнитная индукция поля, создаваемого элементом тока				Idl	в точке, определяемой радиусом-
вектором r .
	R
	Выделим на кольце элемент dl и от него в точку А проведём радиус-вектор r (см. рис. 3.31). Век-
						R
тор	R
тор	dB направим в соответствии с правилом буравчика.					R
						R
	Согласно принципу суперпозиции магнитных полей, магнитная индукция B в точке А определяет-
ся интегрированием:
	R		R
	В = ∫ dB ,

где интегрирование ведётся по всем элементам dl кольца.

Разложим вектор dB на две составляющие: dB , перпендикулярную плоскости кольца, и dB|| , параллельную плоскости кольца, т.е.

dB = dB + dB|| .

Рис. 3.31

Тогда

V V V

B = ∫dB + ∫dB|| .

Заметив, что ∫dB|| = 0 из соображений симметрии и что векторы dB от различных элементов dl со-

направлены, заменим векторное суммирование (интегрирование) скалярным:

B = ∫dB ,

где dB

= dBcosb и dB = m0

Idl

(поскольку dl

перпендикулярен r

и, следовательно, sin α =1 ). Таким обра-

4p r 2

зом,

2πR

I cosb2pR

cosb ∫dl =

B =

4p r

4pr

После сокращения на 2p и замены cosb на R / r получим (см. рис. 3.31)

B = m0 IR2 .

2r 3

Проверим, даёт ли правая часть равенства единицу магнитной индукции, Тл

][I ][R2

]

1 Гн×1 А ×1 м2

1 Гн×1 А2

1 Дж

1 Н ×1 м

= 1 Тл.

[r 3 ]

м×1 м3

1 А ×1 м2

1 А × м2

Здесь мы воспользовались определяющей формулой для магнитной индукции:

B = M max .

Тогда	1 Тл =	1	Н×1 м	.

	1		А×м2

Выразим все величины в единицах СИ и произведём вычисления:

или В = 62,8 мкТл.

Вектор B направлен по оси кольца (пунктирная стрелка на рисунке) в соответствии с правилом буравчика.

Пример 3. На проволочный виток радиусом R = 10 см, помещенный между полюсами магнита, действует максимальный механический момент М = 65 дин×см. Сила тока в витке I = 2 А.

Определить магнитную индукцию B поля между полюсами магнита. Действием магнитного поля Земли пренебречь.

Решение. Индукцию B магнитного поля можно определить из выражения механического момента M , действующего на виток с током в магнитном поле,

uR .

uR||

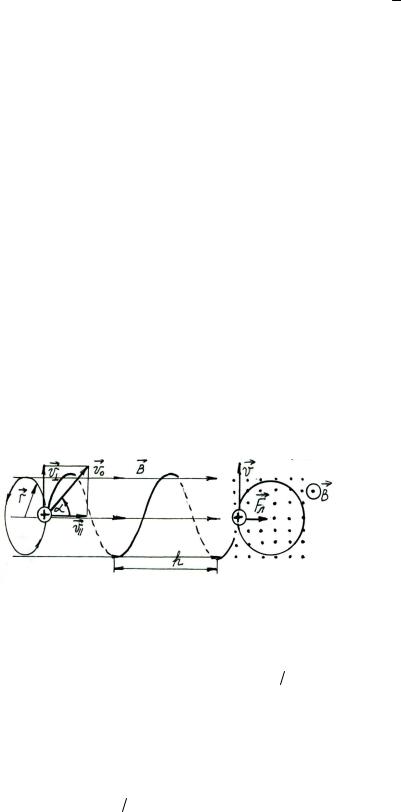
M = pmBsin a ,	(1)
где pm – магнитный момент витка с током; B – индукция магнитного поля; a –	угол между направле-
нием индукции магнитного поля и нормали к плоскости витка.

Если учесть, что максимальное значение механический момент принимает при a = p (sin a = 1) , а так-

					2
же, что магнитный момент витка с током имеет выражение pm = IS , то формула (1) примет вид
	M = IBS .
Отсюда, учитывая, что S = pR2 , находим
				B =	M	.	(2)
				B =		.	(2)
					pR2 I
Подставим числовые значения в формулу (2)
B =	6,5 ×10−6		= 1,04 ×10−4	Тл.
B =	3,14 × 2 ×10	−2	= 1,04 ×10−4	Тл.
		−2

Пример 4. Электрон движется в однородном магнитном поле (В = 10 мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость u.

Решение. Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом (a ¹ p/2) к линиям магнитной индукции. Разложим, как это показано на рис.


3.32, скорость	R	электрона на две составляющие: параллельную вектору			R	R	) и перпендикулярную
3.32, скорость	u0	электрона на две составляющие: параллельную вектору			B ( u\|\|		) и перпендикулярную
R			R	в магнитном поле не изменяется и обеспечивает перемещение электрона вдоль
ему ( u ). Скорость			u\|\|

силовой линии. Скорость uR в результате действия силы Лоренца будет изменяться только по направлению (FЛ ^ uV ) (в отсутствие параллельной составляющей ( u|| = 0) движение электрона происходило бы

по окружности в плоскости, перпендикулярной магнитным силовым линиям). Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью и рав-

номерном движении по окружности со скоростью

Рис. 3.32

Период обращения электрона связан с перпендикулярной составляющей скорости соотношением

T = 2pR u .

(1)

Найдём отношение Ru . Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение a n = u2 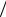R . Согласно второму закону Ньютона, можно написать FЛ = man , или

				e	υ B = mυ 2 / R ,	(2)

где u = u0 sin a .
Сократив (2) на υ , выразим соотношение R u ( R /υ = m / eB ) и подставим его в формулу (1):
T = 2p	m		.

	e	B

Убедимся в том, что правая часть равенства даёт единицу времени, с:

[m]		1 кг		1 кг × А × м2		1 кг × с2 × м2
	=		=		=		= 1 с.
[e][B]	=	1 Кл ×1 Тл	=	1 А × с× Н × м	=	1 с× кг × м2	= 1 с.

Произведём вычисления:

T =

2p × 9,1×10−31

= 3,57 ×10−9 = 3,57 нс.

1,6 ×10

−19

×10 ×10

−3

Модуль скорости u0 , можно выразить через u и u|| :

+ u2 .

Из формулы (2) выразим перпендикулярную составляющую скорости:

Параллельную составляющую скорости

u||

найдём из следующих соображений. За время, равное

периоду обращения Т , электрон пройдёт вдоль силовой линии расстояние, равное шагу винтовой ли-

нии, т.е. h = Tu|| , откуда u|| = h .

Подставив вместо Т правую часть выражения (2), получим

u= е Bh

||p .

2 m

Таким образом, модуль скорости электрона

2 2

u0 = u + u||

Убедимся в том, что правая часть равенства даёт единицу скорости м/с. Для этого заметим, что R и h имеют одинаковую единицу – метр (м). Поэтому в квадратных скобках мы поставим только одну из величин (например, R ):

[e][B] 2

1 Кл×1 Тл 2

1 А× с× Н× м× м 1 Н× с 1 кг× м× с

[R ]2

(м

)

= 1 м/с.

[m]

1 кг

кг× А× м2

1 кг

1 кг × с2

Произведем вычисления:

1,6 ×10−19 ×10 ×10−3

0,06

u0 =

(0,01)

= 2,46 ×10

м/с,

9,1×10−31

или 24,6 Мм/с.

Пример 5. Определить индукцию и напряжённость магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N = 200 витков, идёт ток силой I = 5 А. Внешний диаметр тороида d1 = 30 см, внутренний – d2 = 20 см.

Решение. Для определения напряжённости магнитного поля внутри тороида вычислим циркуляцию вектора H вдоль силовой линии поля:

∫ Hdl .

Из условия симметрии следует, что силовые линии тороида представляют собой окружности и что во всех точках силовой линии численное значение напряжённости одно и то же. Поэтому в выражении циркуляции напряжённость H можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2πr, где r – радиус окружности, совпадающей с силовой линией, вдоль которой вычисляется циркуляция, т.е.

2πr

∫ Hdl = H ∫ dl = 2prH .

Сдругой стороны, в соответствии с законом полного тока циркуляция вектора напряжённости маг-

нитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция:

	n
∫ Hl dl = ∑ Il .		(2)
L	i =1
Приравняв правые части равенства (1) и (2), получим
	n
2prH = ∑ Ii .		(3)

i =1

Силовая линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид

2πrH = NI .

Отсюда

H = NI .

2pr

Для средней линии тороида

r = R1 + R2 = d1 + d 2 .

2 4

Подставив это выражение r в (4), найдём

			H =		2NI					.
			H =	p(d + d		2		)		.
			1			2
Индукция В связана с напряжённостью поля соотношением
	B = mm0 H .
Следовательно,
			B =		2mm0 NI						.
			B =		p(d + d		2		)		.
			1				2
Подставляя числовые значения в (5) и (6), получим
H =	2 × 200 ×5	= 1370	А/м;
H =	3,14(0,3 + 0,2)	= 1370	А/м;

B = 2 × 4p ×10−7 × 200 × 5 = 1,6 ×10−3 Тл. p(0,3 + 0,2)

(4)

(5)

(6)

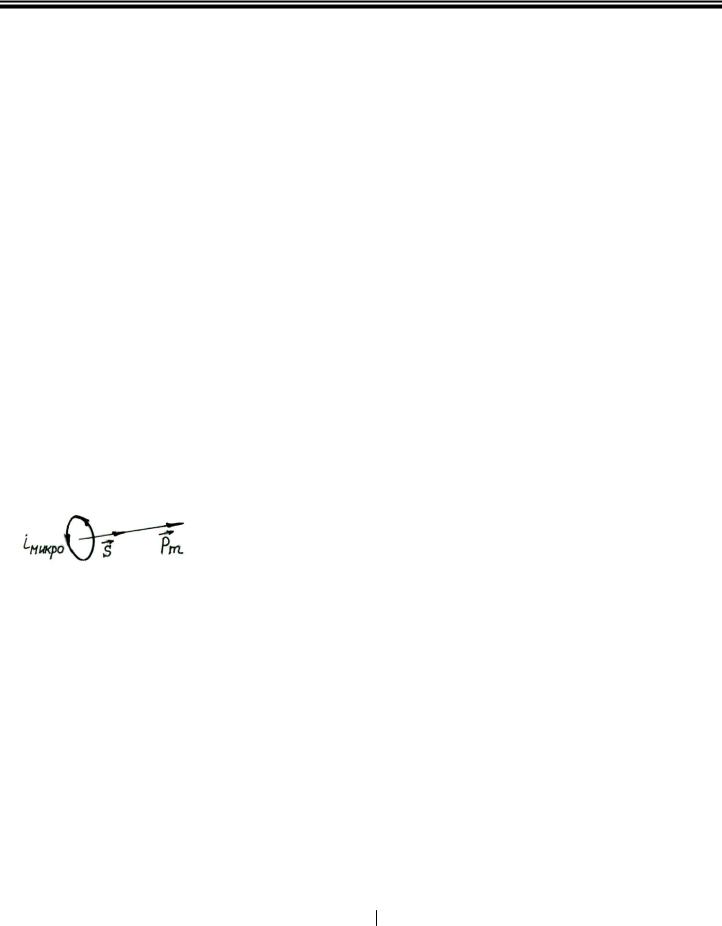
4. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

КЛАССИФИКАЦИЯ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВ

4.1. НАМАГНИЧЕННОСТЬ МАГНЕТИКОВ

Все вещества, помещённые в магнитное поле, намагничиваются, т.е. приобретают вполне определённые магнитные моменты и сами становятся источниками магнитного поля. При этом полное поле B в веществе (усреднённое) складывается из намагничивающего поля B0 и поля, возникшего в веществе

B′ , т.е. B = B0 + B′.

Вещества, способные намагничиваться, называются магнетиками. В зависимости от того, как направлены в каждой точке магнетика поля B′ и B0 и как велико B′ , по сравнению с B0 , все вещества де-

лятся на диамагнетики ( B′ £ B0 , B′ −↓ B0 ), парамагнетики ( B′ £ B0 , B′ -- B0 ) и ферромагнетики ( B′ ³ B0 ,

B′ -- B0 ).

Действие любого из магнетиков можно формально свести к совокупности замкнутых элементарных токов. Ампер назвал их молекулярными токами (или микротоки). Каждый микроток имеет свое магнит-

ное поле, характеризуемое магнитным моментом R (рис. 4.1)

pm = iмикроS ,

где iмикро − микроток; S – вектор, численно равный площади, охватываемой микротоком.

В намагниченном веществе магнитные поля микротоков, складываясь, дают результирующее поле B′ , а магнитные моменты – некоторый результирующий момент.

Магнитное состояние намагниченного вещества характеризуется вектором намагниченности или намагничения.

Рис. 4.1

для неоднородного

Вектор намагниченности J – физическая векторная величина, характеризующая интенсивность намагничивания вещества и равная магнитному моменту единицы объёма вещества.

Для однородного магнетика

		R
R	=	∑ pm	,
J	=	V	,
		V
				∑ pm
				R
	R	= lim		V	.	(4.1.1)
	J			V
	J
		V →0		V

Магнетик называется однородным, если его магнитные свойства одинаковы во всех его точках. Магнетик называется изотропным, если его магнитные свойства одинаковы по всем направлениям. Теория и опыт показывают, что в однородной, изотропной неферромагнитной среде, в не очень

сильных полях и при не очень высоких частотах изменения внешнего поля			R	имеет место соотношение
			B0
			R
R	=	χ	B0	,	(4.1.2)
J
			μ0

где χ – безразмерный коэффициент, зависящий от природы вещества и называемый магнитной воспри-

	R
имчивостью;	B0	и	R	по размерности одинаковы
	B0		J
	μ0		J
	μ0
					B0	=	Н/Ам	= А/м;
					B0		Н/Ам
					μ0		Н/А2

Между магнитной индукцией поля микротоков связь. Установим её.

J	=	Ам2	= А/м.

		м3		R
R
		и вектором намагниченности			существует
B′				J

магнитное

поле

индукцией B0 внесём металлический

стержень, все его микротоки

установятся

перпендикулярно

J .

Рассмотрим

поперечное

се-

чение цилиндра (рис. 4.2).

Смежные

микротоки

компенсируются.

Не

компенсируются

только микротоки во внешнем

слое (10–10 м).

Эти

токи

дают

результирующий

поверхностный

ток,

который и создает поле B′ . Оно

подобно полю соленоида

B′ = μ0 Iмикро,

Рис. 4.2

где Iмикро – поверхностный ток,

приходящийся на единицу длины, или

поверхностная плотность тока (для соленоида B = μ0 NI ).

Микроток i, приходящийся на

отрезок dl цилиндра, равен

i = Iмикроdl ,

его магнитный момент

pm = iS = IмикроdldS ,

где dS − сечение

стержня. Поделив магнитный момент на элементарный объём

dV = dldS , получим магнитный момент единицы объёма, т.е. намагниченность

IмикроdldS

= J

= Iмикро ;

dldS

тогда

B′ = μ0 J ,

(4.1.3)

т.е. векторы

B′ и

совпадают. Учитывая, что J =

(4.1.2),

получим

B′ =

χ B ,

и полное поле в ве-

μ0

ществе станет равным

B = B0

+ B′

= B0

+ χ B0

= (1 +

χ) B0

= μB0 ,

(4.1.4)

где μ −

относительная магнитная проницаемость вещества. Она показывает, во сколько раз изменяется

поле в веществе, по сравнению с вакуумом μ = B / B0.

4.2. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОГО ПОЛЯ

В ВЕЩЕСТВЕ

Установлено, что магнитное поле создается любыми токами, как макроскопическими, так и микротоками. Следовательно, выражение (3.5.1) примет вид

		R	R	= μ0 ∑Iпров + μ0 ∑iмикро .
		∫Bdl		= μ0 ∑Iпров + μ0 ∑iмикро .	(4.2.1)
	R	L
Между вектором намагничения	R	и микротоками iмикро	существует связь. Проведём внутри мате-
Между вектором намагничения	J	и микротоками iмикро	существует связь. Проведём внутри мате-

риала проводника замкнутый контур L (рис. 4.3) и подсчитаем число микротоков, нанизанных на элемент контура dl. Нанизываться будут те токи, центры которых лежат внутри наклонного цилиндра с

площадью основания dS и длиной dl.

При концентрации микротоков n их полное число в цилиндре

	ndV = ndSdl cos α ,
где α – угол между dl и	R
где α – угол между dl и	J . Суммарный ток будет равен iмикроndSdl cos α .

Учитывая, что по определению

		iмикроdSn = pmn = J
	Риc. 4.3	iмикроdSn = pmn = J
	Риc. 4.3	есть вектор намагничения, получаем,	что суммарный микроток, связан-


ный с элементом dl контура обхода, равен
		R R
		iмикроndSdl cos α = Jdl cos α = Jdl ,
		R R
т.е. полный микроток, охватываемый контуром L, будет ∑iмикро = ∫Jdl			и тогда (4.2.1) примет вид

						R R			R R
					∫ Bdl			= μ0 ∑ Iпров + μ0 ∫ Jdl .		(4.2.2)
					L				L
Разделим выражение (4.2.2) на μ0 и объединим интегралы							R
							R
					∫ (		B	R R	= ∑ Iпров ,
							B	− J )dl		(4.2.3)
							μ	− J )dl		(4.2.3)
					L	0
	R				L
	R
	B		R	R
где выражение	B		− J	= H	называется напряжённостью магнитного поля. Единицей напряжённости яв-
где выражение	μ	0	− J	= H
	μ

ляется А/м, что следует из (4.2.3) H м = А , откуда Выполнив замену в (4.2.3), получим

H = A/м .

R R	= ∑ I пров .
∫ Hdl	= ∑ I пров .	(4.2.4)

Выражение (4.2.4) называется законом полного тока или теоремой о циркуляции вектора напряжённости магнитного поля.

Циркуляция вектора напряжённости стационарного магнитного поля равна полному току проводимости, протекающему через любую поверхность, опирающуюся на контур интегрирования.

Таким образом,		R	R
Таким образом,		для характеристики магнитного поля введены два вектора B	и H . Основным явля-
ется	R	R
ется	B . Поскольку	H зависит от макротоков, то по ним легче следить за изменениями поля.
	R		R
	H зависит от среды μ, в ограниченных магнетиках – от их формы и размеров.		H не зависит от сре-

ды, когда однородная среда заполняет всё пространство поля или эта среда не пересекается с линиями внешнего поля.

Рассмотрим примеры определения напряженности поля в магнетиках. 1. Напряжённость магнитного поля в вакууме.

R′

Так как для вакуума J = 0 , то и

B = 0 . Следовательно,

B =

′ = B0

H0 =

− J =

(4.2.5)

μ0

делённому на μ0 .

Напряжённость магнитного поля в вакууме

0 равна B0 ,

2. Напряжённость магнитного поля в безграничной однородной изотропной среде.

Рассмотрим безграничный соленоид. Если в нём сердечника нет,

то H0

= B0 / μ0.

После заполне-

R′

ния соленоида однородным изотропным веществом H =

− J =

+ B

− J , но так как

′

= μ0 J (4.1.3),

μ0

то,

= B0 / μ0 , т.е. поле в однородном изотропном магнетике равно полю в вакууме

H = H 0 (4.2.5)

совпадает с напряжённостью внешнего поля. Для изотопной неферромагнитной среды связь между B

проста, так как B0

= μ0 H ,

то из B = μB0 следует, что

B = μ0μH.

(4.2.6)

3. Напряжённость поля в ограниченных магнетиках.

Рассмотрим бесконечно длинный соленоид с однородным, изотропным сердечником. Удалим части А и Б (рис. 4.4).

АБ

Рис. 4.4

	R			R	R	R
Тогда индукция B1		станет меньше		B , а так как	B1 <	B , то и напряжённость поля в коротком сер-
R	R						R R	R	R
дечнике H1	= B1 / μ0μ будет меньше напряжённости поля длинного сердечника						H = B / μ0μ , т.е. H1 <		H , но
R R		R	R
H = H0 , следовательно,		H1 <	H0 .

В ограниченных магнетиках напряжённость магнитного поля меньше напряжённости внешнего по-

ля.

4.3. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ ВЕКТОРОВ H И B

Для ограниченных магнетиков большое значение приобретают граничные условия, определяющие поведение B и H на границе раздела сред. Эти условия вытекают из теоремы о циркуляции вектора напряжённости и теоремы Гаусса для вектора индукции.

На границе раздела двух магнетиков с магнитными проницаемостями μ1 и μ2 вырежем небольшой цилиндр так, чтобы его образующая была перпендикулярна границе раздела магнетиков (рис. 4.5).

Рис. 4.5

Для рассматриваемого цилиндра по теореме Гаусса поток Ф равен нулю,

				Ф = Bn	2	S − Bn	S = 0 ,
					2	1
откуда	Bn	2	= Bn	,			(4.3.1)
		2	1

нормальные составляющие вектора индукции при переходе границы раздела магнетиков не изменяются.

Выразив вектор индукции через напряжённость поля, получим

μ0μ1Hn1 = μ0μ2 Hn2 ,

откуда

Hn		=	μ	2 .	(4.3.2)
	1
H
	n2		μ
				1

Вычислим циркуляцию вектора напряжённости (в проекции на выбранное направление) по прямоугольному контуру, стороны которого параллельны границе раздела магнетиков (рис. 4.6)

∫ Hdl = Hτ1 l − Hτ 2 l = ∑ I = 0 ,

так как контур обхода не охватывает токов.

		Рис. 4.6
Из последнего равенства получаем
			H τ2 = H τ1 ,					(4.2.3)
	R	R
еще раз учитывая, что	B = μ0μH , имеем
			Bτ1	=	μ1		.	(4.2.4)
			B	=			.	(4.2.4)
			B		μ	2
			τ2			2

Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая

R R

вектора индукции Bn и тангенциальная составляющая вектора напряжённости Hτ не изменяется; тан-

генциальная составляющая вектора индукции Bτ и нормальная составляющая вектора напряжённости Hn изменяются скачкообразно (рис. 4.7).

Рис. 4.7

МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА

4.4.МАГНИТНЫЕ МОМЕНТЫ АТОМОВ И МОЛЕКУЛ

1.Согласно представлениям классической физики электроны в атомах движутся по замкнутым орбитам. Следовательно, каждый электрон создаёт замкнутый микроток, магнитное поле которого можно охарактеризовать магнитным моментом (рис. 4.8).

обусловленный движением электрона по

Магнитный

момент pm ,

орбите,

называется

орбитальным

магнитным

моментом

электрона.

Величина

орбитального

магнитного момента электрона равна

pm = iS ,

где i – ток,

создаваемый

Рис. 4.8

электроном; S –

площадь орбиты.

Будем считать орбиту круговой. Через любое сечение электронной орбиты за единицу времени переносится заряд eν , где e – заряд электрона; ν – число оборотов в секунду. Следовательно, созданный электроном ток равен i = eν . Частоту обращения ν можно выразить через линейную скорость υ

ν =	υ	,
ν =		,
	2πr
где r – радиус орбиты. Площадь орбиты равна S = πr 2 .
Таким образом
		pm	= iS =	eυr	.	(4.4.1)
		pm	= iS =		.	(4.4.1)
			2

Так как заряд электрона отрицателен, направление движения электрона и направление создавае-

мого им тока противоположны. Направление вектора R образует с направлением тока правовинтовую, pm

а с направлением движения электрона левовинтовую систему (рис. 4.8).

Движущийся по орбите электрон обладает моментом импульса, который принято называть орбитальным механическим моментом

	R	R	(4.4.2)
	L = [r mυ],		(4.4.2)
где r – радиус-вектор электрона (рис. 4.8).
R
Модуль вектора	R
Модуль вектора	L равен
так как угол между r	L = rmυ ,		(4.4.3)
так как угол между r	и υ все время прямой.
R

Отношение модулей векторов орбитального магнитного и орбитального механического моментов

называется орбитальным гиромагнитным отношением электрона
				pm	= g.	(4.4.4)
					= g.	(4.4.4)
				L
Учитывая направления	R	и	R
Учитывая направления	pm	и	L ,

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1511 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.05.2015986.45 Кб52ankudimova.pdf
#
22.05.2015758.09 Кб13Ankudim_c.pdf
#
21.05.20151.16 Mб12anologi.doc
#
20.03.20163.16 Mб39Antsiferov.pdf
#
11.07.2019142.34 Кб12Appendix.doc
#
22.05.20155.26 Mб11barsukov-a.pdf
#
21.09.20193.4 Mб9BARSUKOV.doc
#
22.05.20152.97 Mб85baryshev-s.pdf
#
22.05.2015100.86 Кб270bazafilosofia.docx
#
21.05.201510.41 Mб82Baza_po_fizike_3_semestr.doc
#
21.05.2015832.51 Кб69baza_po_istorii.doc