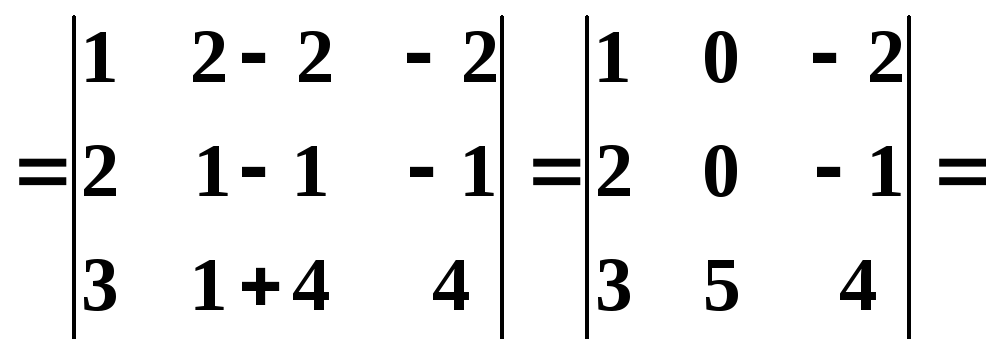- •Фгоу впо «Волгоградская академия государственной службы»
- •1.2. Цели и задачи учебной дисциплины.
- •1.3. Требования к уровню освоения дисциплины (знания, умения, навыки).
- •1.4. Тематический план курса «математика» (174 ч.)
- •1.5. Учебно-методическое обеспечение учебной дисциплины
- •Тема 6. Понятие функции. Способы задания и основные свойства функций.
- •Тема 7. Предел последовательности и функции. Правила вычисления пределов.
- •Тема 8. Замечательные пределы. Непрерывность функции. Основные теоремы о непрерывных функциях. Точки разрыва и их классификация.
- •Тема 9. Задачи, приводящие к производной. Понятие производной функции.
- •Тема 10. Производная неявных и параметрических функций. Производные высших порядков.
- •Тема 11. Понятие дифференциала функции.
- •Тема 12. Основные теоремы о дифференцируемых функциях. Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя-Бернулли раскрытия неопределенностей вида и.
- •Тема 13. Полное исследование функций и построение графиков.
- •Тема 14. Первообразная и неопределенный интеграл. Свойства интеграла. Таблица неопределенных интегралов.
- •Тема 15. Основные методы интегрирования.
- •Тема 16. Понятие определенного интеграла. Свойства и правила вычисления определенного интеграла.
- •Тема 17. Приложения определенного интеграла. Несобственные интегралы.
- •Планы семинарских и практических занятий
- •Тема 1. Операции над матрицами. Определители третьего порядка. (2 часа)
- •Тема 2. Определители четвертого и выше порядков. Элементарные преобразования определителей. Обратная матрица. (4 часа)
- •Тема 3. Ранг матрицы.(4 часа)
- •Тема 8. Замечательные пределы. Основные эквивалентные функции (4 часа).
- •Тема 9. Определение производной. Геометрический смысл. Основные правила дифференцирования. Таблица производных элементарных функций.(2 часа)
- •Тема 10. Производные неявных и параметрических функций. Логарифмическое дифференцирование. Производные высших порядков.(2 часа)
- •Тема 11. Дифференциал функции. Приложение производной в теории пределов. (2 часа)
- •Тема 12. Общая схема исследования функций и построения их графиков.(2 часа)
- •Тема 13. Контрольная работа.(2 часа)
- •Тема 14. Неопределенный интеграл. Свойства неопределенного интеграла. Интегралы от основных элементарных функций. Основные методы интегрирования.(2 часа)
- •Тема 15. Основные методы интегрирования: интегрирование по частям.(2 часа)
- •Тема 16. Определенный интеграл. Формула Ньютона-Лейбница. Методы интегрирования. Геометрические приложения определенного интеграла. (4 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Основы теории множеств.
- •Тема 2. Элементы аналитической геометрии.
- •Вопросы к зачету:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1
- •Тема 19. Экстремум функций нескольких переменных. Наибольшее и наименьшее значения функции. Условный экстремум.
- •Тема 20. Условный экстремум функций нескольких переменных.
- •Тема 21. Основные понятия теории дифференциальных уравнений. Дифференциальные уравнения первого порядка.
- •Тема 22. Линейные неоднородные дифференциальные уравнения первого порядка.
- •Тема 23. Линейные однородные дифференциальные уравнения второго порядка. Линейные неоднородные дифференциальные уравнения второго порядка с правой частью специального вида.
- •Тема 24. Линейные неоднородные дифференциальные уравнения второго порядка. Метод Лагранжа.
- •Тема 30. Алгебра событий. Теоремы сложения и умножения вероятностей событий.
- •Тема 31. Формула полной вероятности. Формула Байеса.
- •Планы семинарских и практических занятий
- •Тема 1. Функции нескольких переменных. Частные производные. Дифференциал. (4 часа)
- •Тема 2. Экстремум функций двух переменных. Наибольшее и наименьшее значения функции. (2 часа)
- •Тема 3. Дифференциальные уравнения. Общее решение дифференциального уравнения. Задача Коши. (2 часа)
- •Тема 4. Линейные неоднородные дифференциальные уравнения первого порядка. (2 часа)
- •Тема 5. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Уравнения однородные. Неоднородные уравнения с правой частью специального вида. (4 часа)
- •Тема 6. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа. (4 часа)
- •Тема 7. Числовые ряды. Определение сходимости ряда. Основные свойства рядов. Необходимый признак сходимости числового ряда.Достаточные признаки сходимости знакоположительных рядов. (4 часа)
- •Тема 8. Знакочередующиеся ряды. Теорема Лейбница.(2 часа)
- •Тема 9. Понятие функционального ряда. Область сходимости. Степенной ряд. Интервал и радиус сходимости степенного ряда.(2 часа)
- •Тема 10. Разложение функций в степенные ряды. Формула и ряд Тейлора. Формула и ряд Маклорена. Применение рядов в приближенных вычислениях. (2 часа)
- •Тема 11. Контрольная работа. (2 часа)
- •Тема 12. Классическое определение вероятности. Элементы комбинаторики. Алгебра событий. Теоремы сложения и умножения вероятностей. (2 часа)
- •Тема 13. Формула полной вероятности. Формула Байеса. (2 часа)
- •Тема 14. Последовательность независимых испытаний. Наивероятнейшее число появлений события в серии из n независимых испытаний. Асимптотические формулы.(2 часа)
- •Тема 15. Контрольная работа.(2 часа)
- •Тема 16. Дискретная и непрерывная случайная величина. Закон распределения. Числовые характеристики.(2 часа)
- •Тема 17. Классические законы распределения случайных величин. Биномиальный закон. Равномерное и показательное распределение. Нормальная случайная величина.(2 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Самостоятельное решение задач по теории дифференциальных уравнений и теории рядов.
- •Тема 2. Самостоятельное решение задач по теории вероятностей.
- •Вопросы к экзамену:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1 Примерный вариант заданий
- •Контрольная работа № 2 Примерный вариант заданий
- •Примерный вариант экзаменационного билета
- •Список рекомендуемой литературы
- •Раздел 2. Методические рекомендации по изучению учебной дисциплины для студентов
- •2.1. Рекомендации по использованию материалов учебно-методического комплекса:
- •2.2. Пожелания к изучению отдельных тем курса
- •2. 3. Рекомендации по работе с литературой
- •2.4. Советы по подготовке к экзамену (зачету)
- •Раздел 3. Материалы тестовой системы или практикум по решению задач по темам лекций
- •Iсеместр
- •Примеры решения задач по темам 1 – 5
- •Примерный вариант практического задания по Темам 1 – 5.
- •Примеры решения задач по темам 6 – 13
- •Примерный вариант практического задания по Темам 6 – 13.
- •Примеры решения задач по темам 14 – 17
- •Примерный вариант практического задания по Темам 14 – 17.
- •IIсеместр
- •Примеры решения задач по темам 18 – 24
- •Примерный вариант практического задания по Темам 18 – 24.
- •Примеры решения задач по темам 25 – 28
- •Примерный вариант практического задания по Темам 25 – 28.
- •Примеры решения задач по темам 29 – 35
- •Примерный вариант практического задания по Темам 29 – 35.
- •Раздел 4. Словарь основных терминов (глоссарий)
2. 3. Рекомендации по работе с литературой
Очень важную роль играет выбор учебной литературы и методических пособий. Желательно придерживаться этих учебников при изучении всего курса, так как замена может привести к утрате логической связи между отдельными темами.
В последние годы среди студентов экономических специальностей особой популярностью пользуется следующая литература:
Высшая математика для экономистов. / Под.ред. Н.Ш. Кремера.-М.: Банки и биржи, 1997.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. -М.: Наука, 1986.
Карасев А.Н., Аксютина З.М., Савельева Т.Н. Курс высшей математики для экономических вузов. Ч1 и 2.-М.: Высшая школа, 1986.
Красс М.С. Математика для экономических специальностей. -М.:Инфра-М, 1998.
Исследование операций в экономике. / Под.ред. Н.Ш.Кремера. -М.: Банки и биржи, 1997.
Практикум по высшей математике для экономистов. / Под.ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2002.
2.4. Советы по подготовке к экзамену (зачету)
Фундамент математических знаний закладывается на лекционных и семинарских занятиях, а также при подготовке к ним. Буквально с первого сентября необходимо выработать серьезное отношение к конспекту по математике. Он должен в полном объеме содержать определения, теоремы и выводы основных формул курса. Записи должны быть аккуратными. Не нужно забывать, что они делаются для того, чтобы впоследствии с ними работать. Все теоремы и факты нужно понять, а поняв, уметь их самостоятельно доказывать. Прочитав доказательство какой-то теоремы, воспроизвести это доказательство на бумаге без конспекта или учебника.
Помните, что умение решать задачи является следствием глубоко понятого соответствующего теоретического материала. Учебник нужно не просто читать, а изучать; основой запоминания является понимание, знание забывается – понимание никогда; повторение – важнейшее средство, предотвращающее забывание; необходимо выработать привычку систематической самостоятельной работы, «натаскивание» к экзамену или зачету дает слабый и поверхностный результат.
Для успешной сдачи зачета и экзамена студент должен знать наизусть достаточно солидный объем теорем, формул, алгоритмов, моделей. Не откладывая процесс заучивания на последние три дня перед экзаменом, подготовка должна вестись с первых лекций. Будет очень хорошо, если вы заведете себе личный справочник и будете его регулярно изучать, пополняя новым материалом.
Раздел 3. Материалы тестовой системы или практикум по решению задач по темам лекций
Iсеместр
Примеры решения задач по темам 1 – 5
Пример 1.
Вычислить
определитель
 :
:
а) разложив его по элементам первого столбца;
б) предварительно упростив с помощью элементарных преобразований.
Решение:а) Разложим заданный определитель по элементам первого столбца, которые равны a11 = 1, a21 = 2, a31 = 3. Вычислим алгебраические дополнения этих элементов:
![]() ,
,
![]() ,
,
![]() ,
так как первая строка пропорциональна
второй.
,
так как первая строка пропорциональна
второй.
Итак, применяя теорему Лапласа, получаем:
∆ = a11 A11 + a21 A21 + a31 A31 = 1 5 +2 (‑10) + 3 0 = ‑15.
б) упростим определитель с помощью элементарных преобразований.
|
|
Сложим элементы второго и третьего столбцов. Результат запишем во второй столбец. |
|
|
Разложим этот определитель по элементам второго столбца, т. к. в нём содержится два нуля. |
|
|
Вычислим определитель 2-го порядка. |
![]() . Ответ:
обоими способами получили ∆ = ‑15.
. Ответ:
обоими способами получили ∆ = ‑15.
Пример 2.
Вычислить определитель четвёртого порядка
.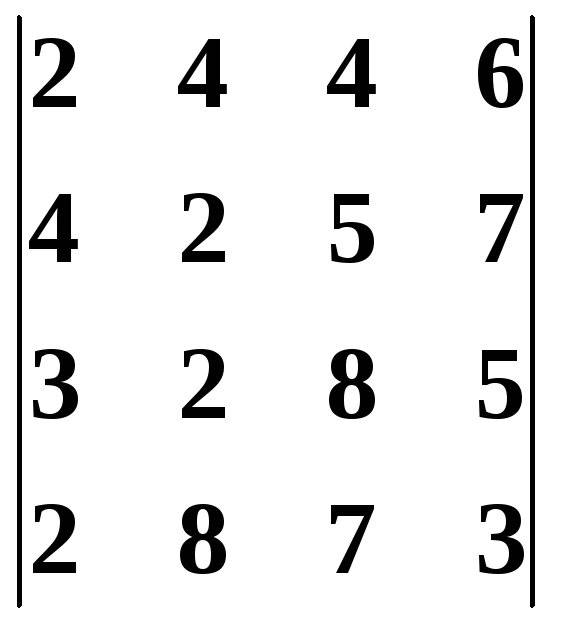 Решение.
Выполним следующие элементарные
преобразования. Из второго столбца
вычтем третий. Получим:
Решение.
Выполним следующие элементарные
преобразования. Из второго столбца
вычтем третий. Получим:
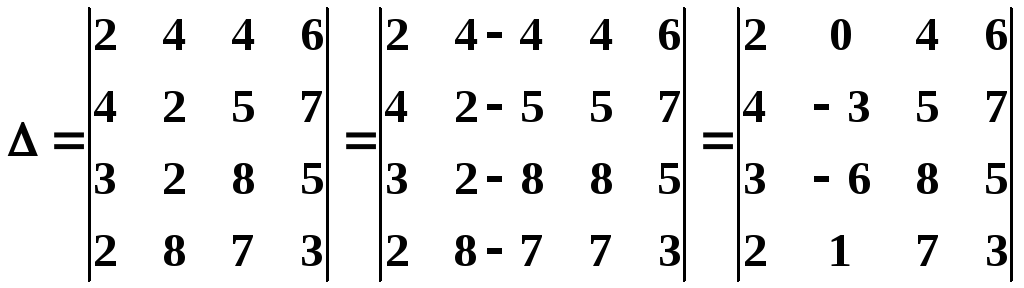 .
.
Затем из третьего столбца вычтем удвоенный первый:
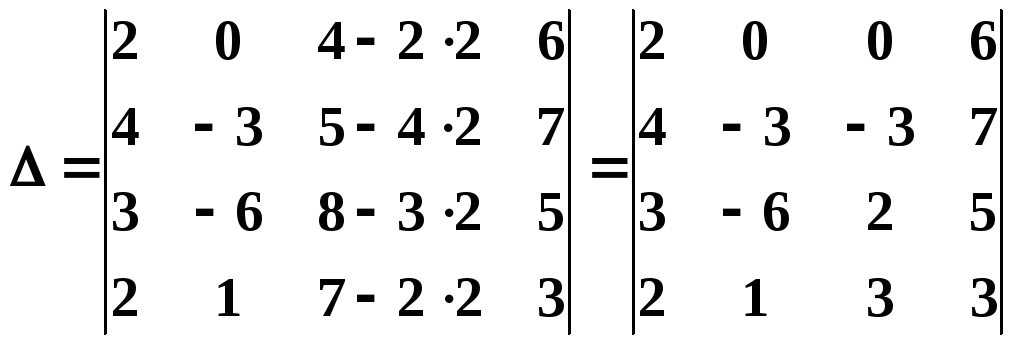 .
.
Из четвёртого столбца вычтем утроенный первый:
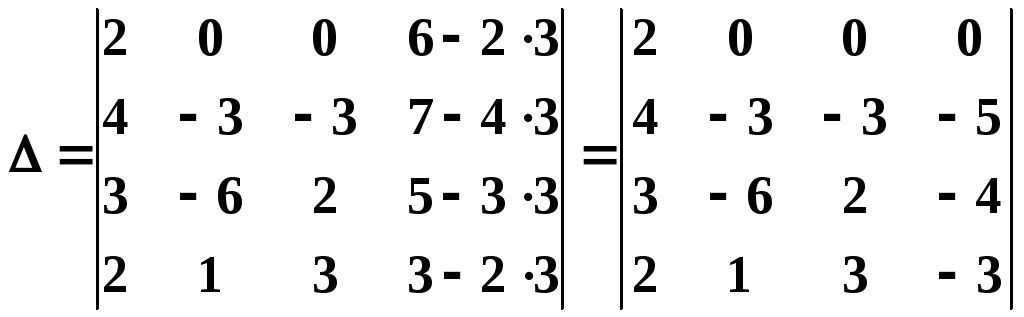 .
.
Разложим этот определитель по элементам 1-й строки:
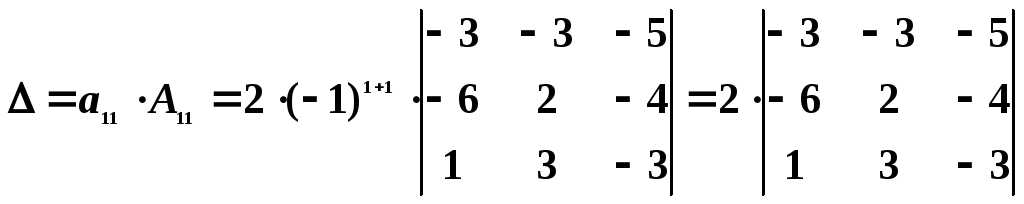 .
.
Сложим второй и третий столбцы, получим:
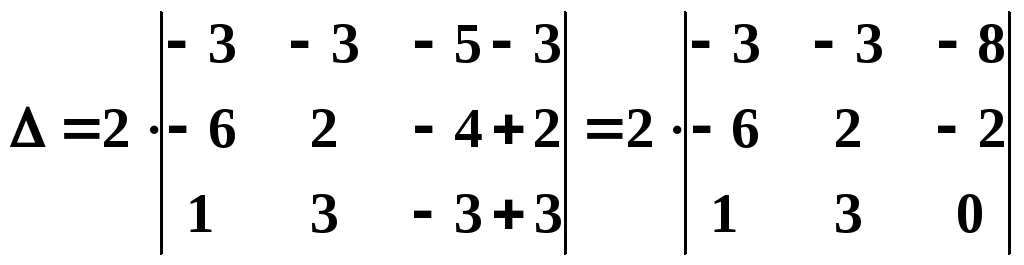 .
.
Из второго столбца вычтем утроенный первый и разложим определитель по элементам третьей строки:
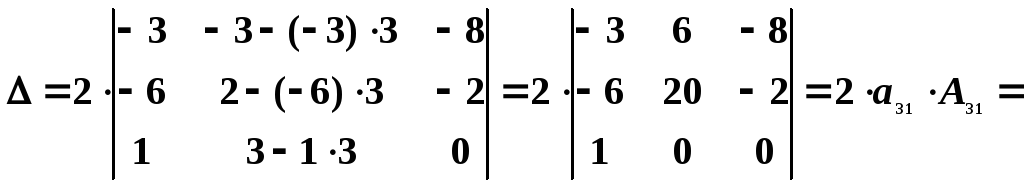
![]() .
.
Ответ: ∆ = 296.
Пример 3.
Для
матрицы
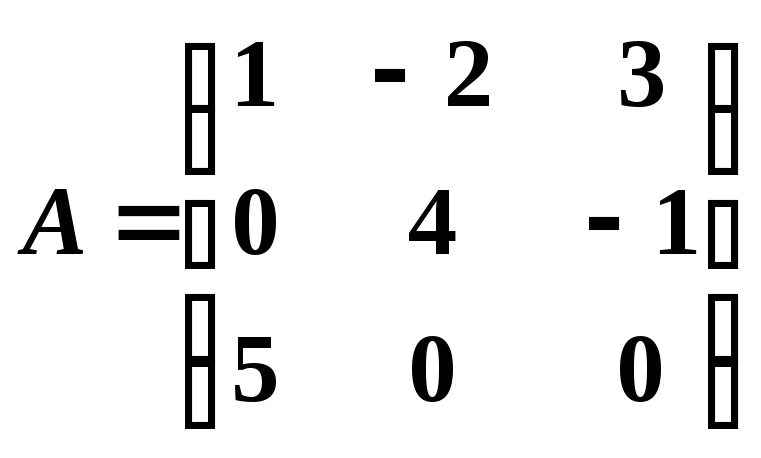 найти обратную.
найти обратную.
Решение.Сначала запишем транспонированную матрицу:
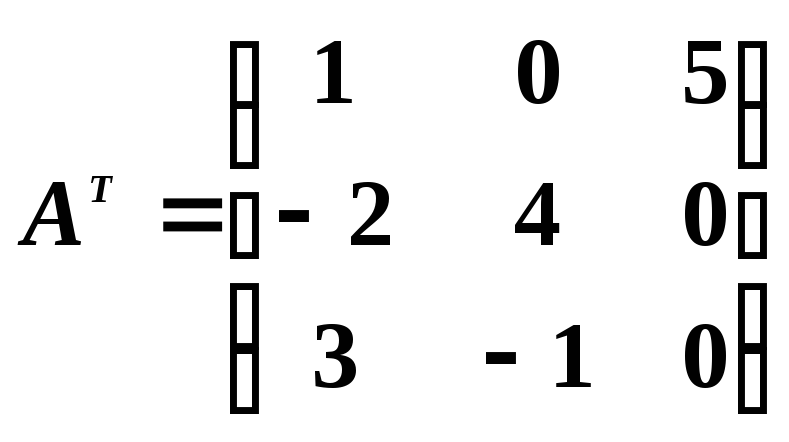 .
.
Находим присоединенную матрицу. По определению, элементами присоединенной матрицы являются алгебраические дополнения элементов транспонированной матрицы. Вычислим элементы присоединенной матрицы.
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Таким образом, матрица, присоединенная к матрице A, имеет вид:
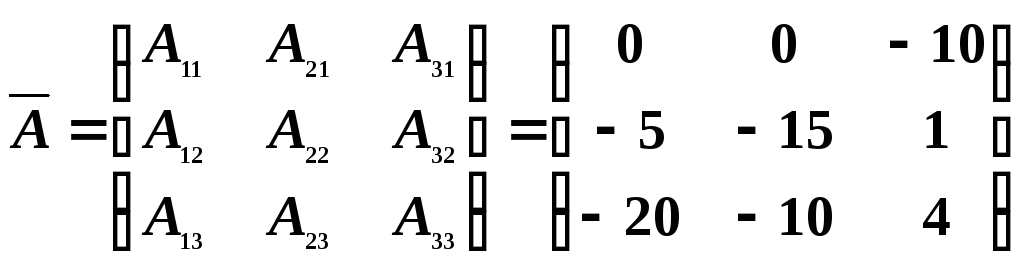 .
.
Пользуясь
правилом треугольников, найдем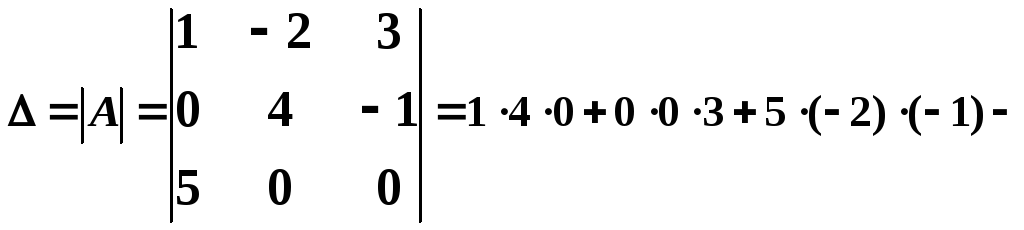
![]() .
.
Так
как
= –50
0, то матрица — неособенная и для неё
существует обратная
![]() .
.
Подставляя найденные определитель и присоединённую матрицу, находим обратную матрицу:

 .
.
Нам осталось сделать проверку, используя то свойство, что произведение заданной матрицы A и найденной обратной A‑1 должно равняться единичной матрице, т. е. A A-1= E.
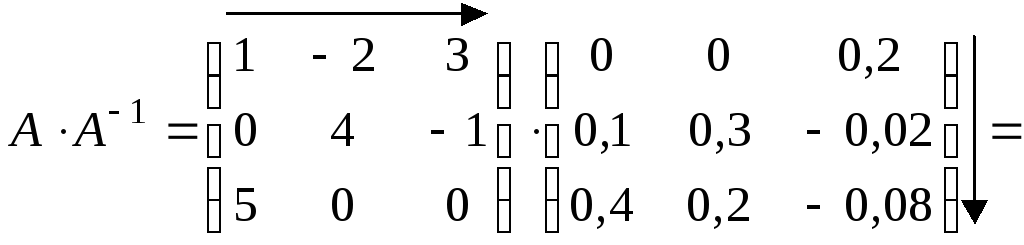
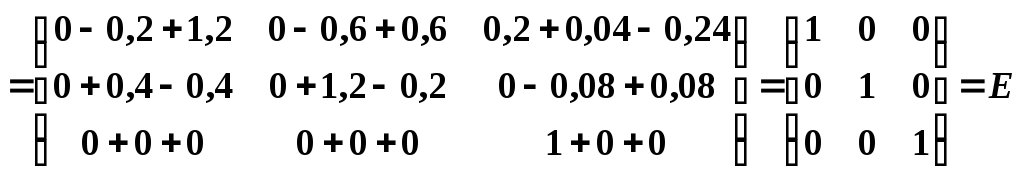 ,
,
следовательно, обратная матрица найдена верно.
Ответ:
 .
.
Пример 4. Определить ранг матрицыА=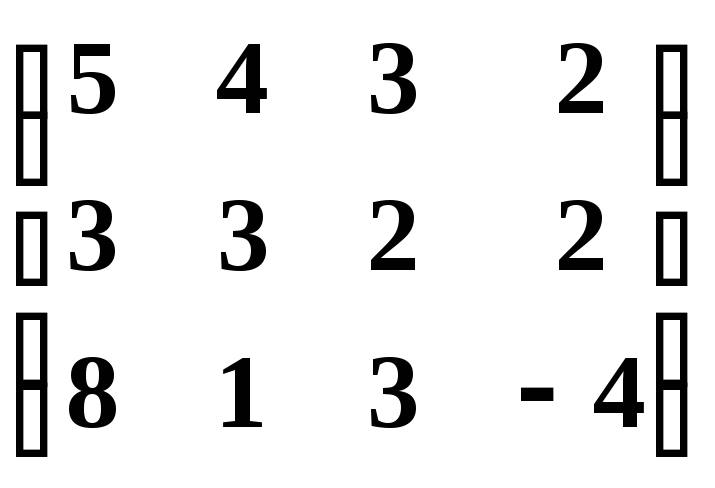 .
.
Решение.
В левом
верхнем углу матрицы минор второго
порядка отличен от нуля
![]() .
Два минора третьего порядка, которые
его окаймляют равны:
.
Два минора третьего порядка, которые
его окаймляют равны:
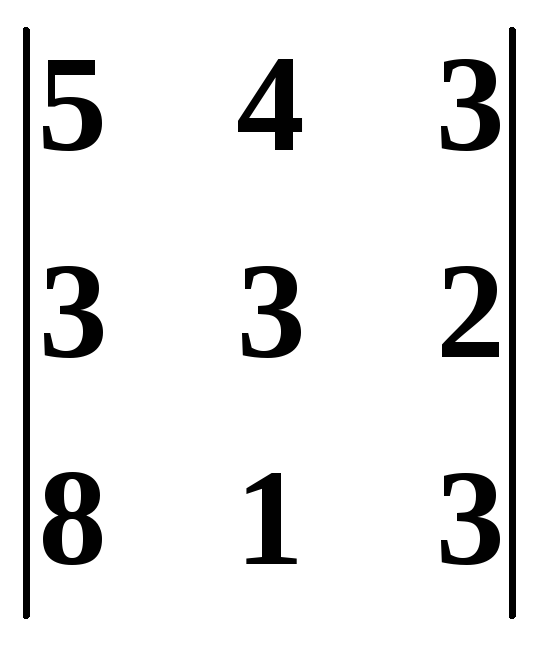 =
118 – 118 = 0,
=
118 – 118 = 0,
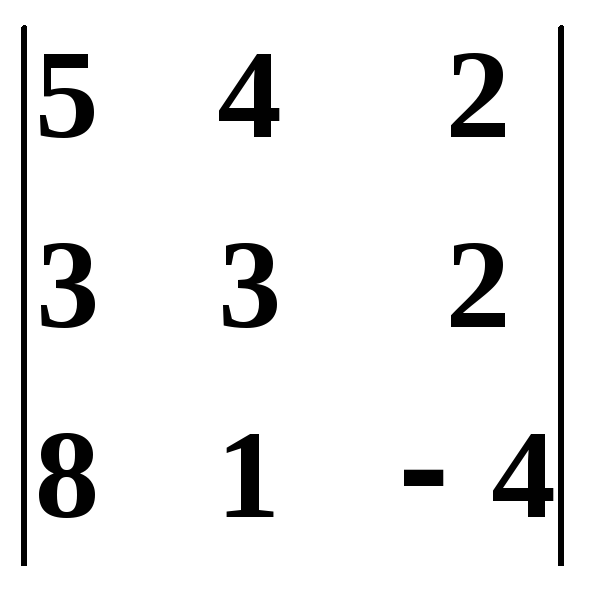 = 10 – 10 = 0.
= 10 – 10 = 0.
Как видно, они нулевые, поэтому r(A) = 2. Ответ: r(A) = 2.
Пример 5. Применяя метод Гаусса, решить систему уравнений:
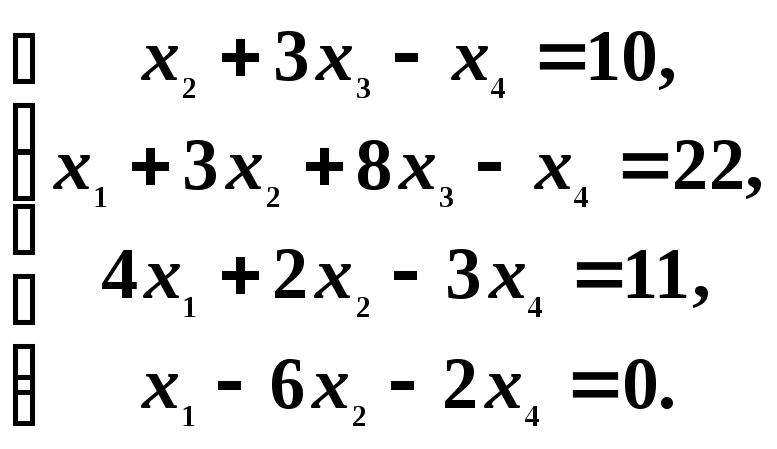
Решение. С помощью одного из уравнений надо исключить из всех последующих уравнений переменную x1. Поменяем местами первое уравнение со вторым, тогда получим:
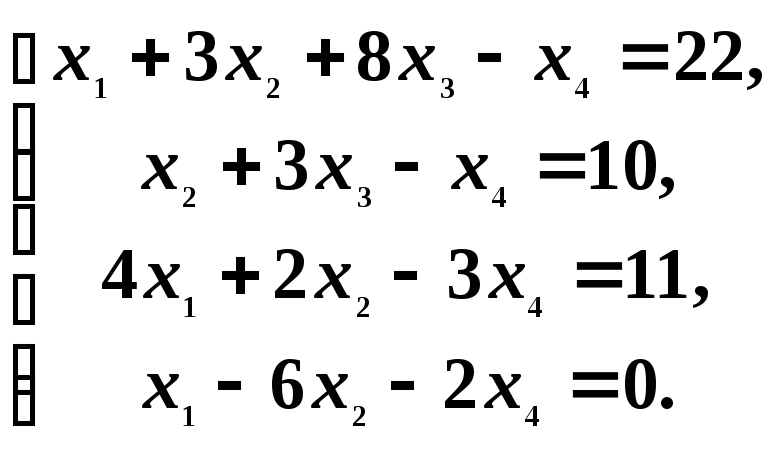
Шаг 1. Так как а11 = 1 0, можно исключить с помощью первого уравнения переменную x1 из последующих уравнений. Как видно из системы, второе уравнение не содержит переменную x1.Чтобы с помощью первого уравнения исключить переменную x1 из третьего уравнения, умножим первое уравнение на (-4) и прибавим полученное уравнение к третьему уравнению:
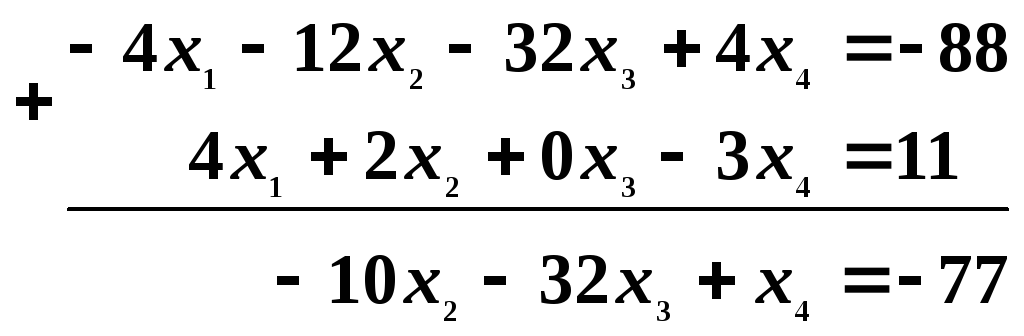 .
.
Это уравнение записываем вместо третьего. Теперь исключаем x1 из четвертого уравнения. Для этого первое уравнение умножаем на (-1) и складываем с четвертым:
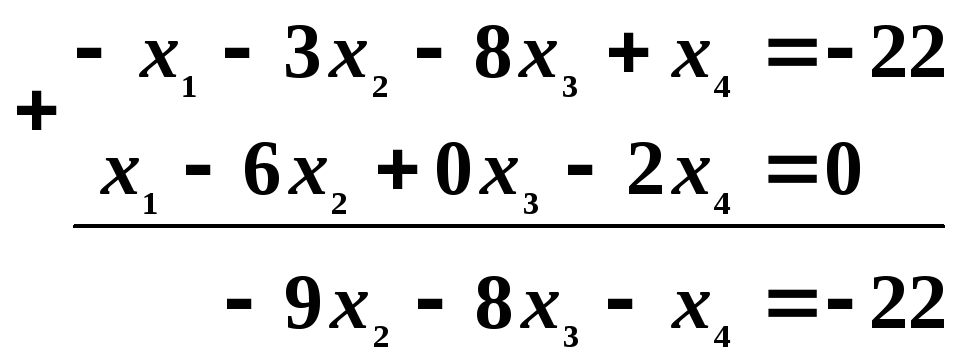 .
.
Записываем полученное уравнение в четвертой строке новой системы. Сохраняем первое и второе уравнения без изменения, а третье и четвёртое записываем в преобразованном виде, получим:
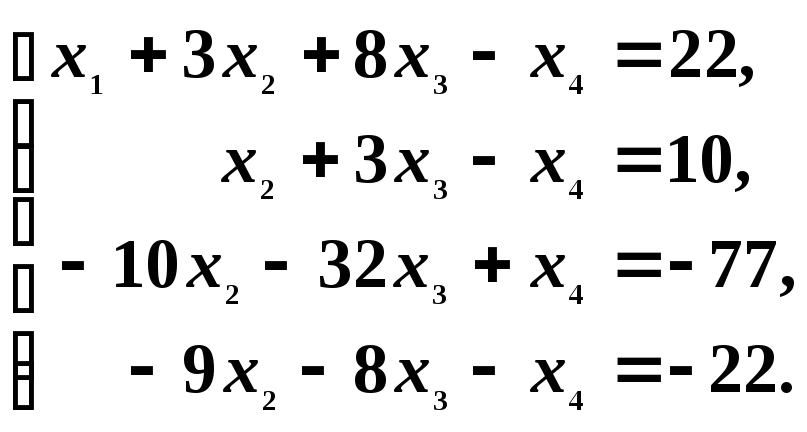
Шаг 2. Рассмотрим новую систему. Здесь а22 = 1 0, следовательно, можно, оставляя без изменения первое уравнение новой системы, с помощью второго уравнения исключить переменную x2 из последующих. Для этого к третьему уравнению прибавляем второе, умноженное на 10, а к четвёртому — второе, умноженное на 9. В результате получим систему:
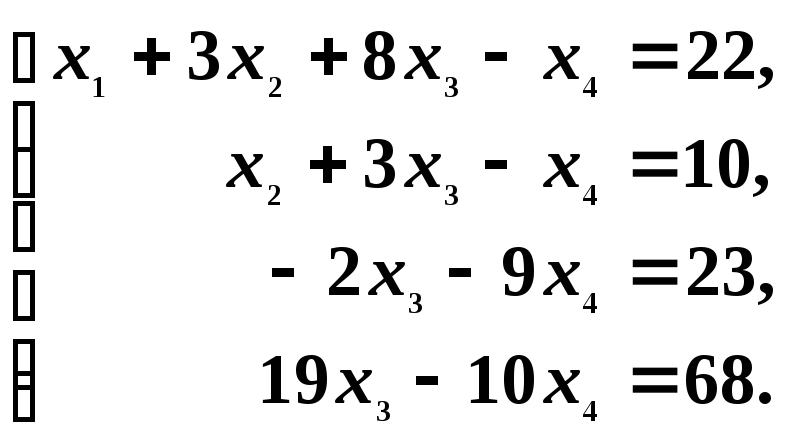
Шаг 3. Сохраняя первые два уравнения новой системы без изменения, с помощью третьего уравнения исключаем переменную x3 из последнего уравнения. Это возможно, так как а33 = ‑2 0. Прибавим к четвертому уравнению третье, умноженное на 19/2 = 9,5. В результате приходим к системе треугольной формы, содержащей четыре уравнения и четыре переменные:
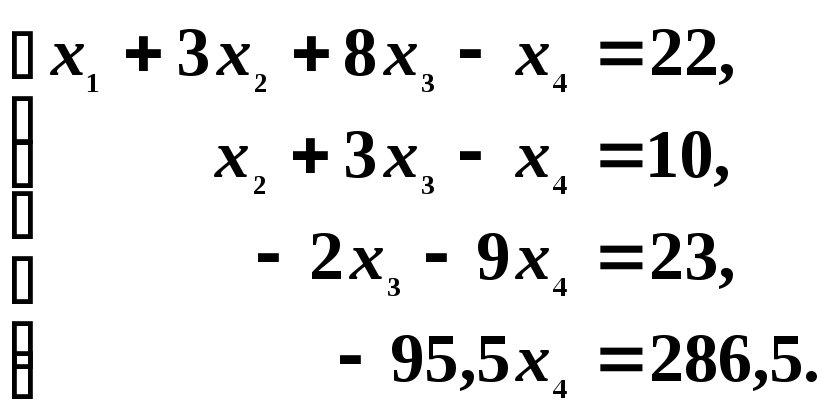
Следовательно, полученная и исходная системы являются совместными. Искомое решение находим, используя обратный ход метода Гаусса, т.е. все неизвестные определяются последовательно, начиная с последнего уравнения. Из четвёртого уравнения находим:
x4 = 286,5 / (-95,5) = -3. Это значение x4 = -3.
Подставляем в третье уравнение системы и получаем:
-2x3 ‑9(‑3) = 23, отсюда x3 = 2.
Далее, подставляем значения x3 и x4 во второе уравнение системы:
x2 + 32 ‑ (‑3) = 10, тогда x2 = 1.
Наконец, подстановка значений x2, x3, x4 в первое уравнение даёт:
x1 +31 +82 ‑ (‑3)=22, откуда x1 = 0.
Итак, данная система уравнений совместна и имеет единственное решение
x1 = 0; x2 = 1; x3 = 2; x4 = -3.