Тема 7. Интегральное исчисления функций

одной переменной.

Основные теоретические сведения.

1. Неопределенным интегралом от функции называется выражение видаесли. Функция называется первообразной для заданной функции .

2. Свойства неопределенного интеграла.

1)

2)

3)

4) где

5)

3. Таблица основных неопределенных интегралов.

1. где().

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

4. Методы интегрирования.

При интегрировании наиболее часто используются следующие методы.

1) Если то

(1)

где а и b–некоторые постоянные.

2) Подведение под знак дифференциала:

(2)

так как

3) Формула интегрирования по частям:

(3)

Обычно выражение выбирается так, чтобы его интегрирование не вызывало особых затруднений. За, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида , где–многочлен отх.

4) Интегрирование рациональных дробей, т.е. отношений двух многочленов и(соответственной иnй степени): сводится к разложению подынтегральной функциина элементарные, всегда интегрируемые дроби вида:

, (4)

где l и m –целые положительные числа, а трехчлен не имеет действительных корней. При этом в случае неправильной дроби () должна быть предварительно выделена целая часть.

5) Интегрирование методом замены переменной (способом подстановки) является одним из эффективных приемов интегрирования. Его сущность состоит в переходе от переменной х к новой переменой t: . Наиболее целесообразная для данного интеграла замена переменной, т.е. выбор функции , не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные подстановки:

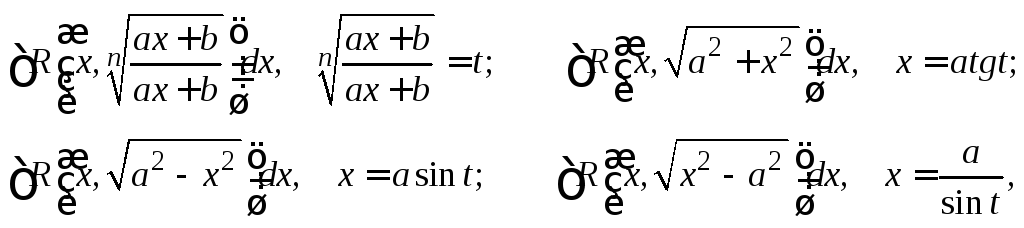
где R– символ рациональной функции.

2. Формула Ньютона-Лейбница для вычисления определенного интеграла имеет вид:

(5)

если и первообразнаянепрерывна на отрезке.

Определенный интеграл численно равен площади криволинейной трапеции, ограниченной прямыми x=a, x=b, y=0 и частью графика функции взятой со знаком плюс, если, и со знаком минус, если.

Пример 1. Найти .

Решение. Так как то, используя формулы (1), получим

Проверка:

Пример 2. Найти .

Решение. Так как , то по формуле (2) находим

Пример 3. Найти .

Решение. Применим метод интегрирования по частям. Положим ,тогда. Используя формулу (3), имеем

.

Пример 4. Найти .

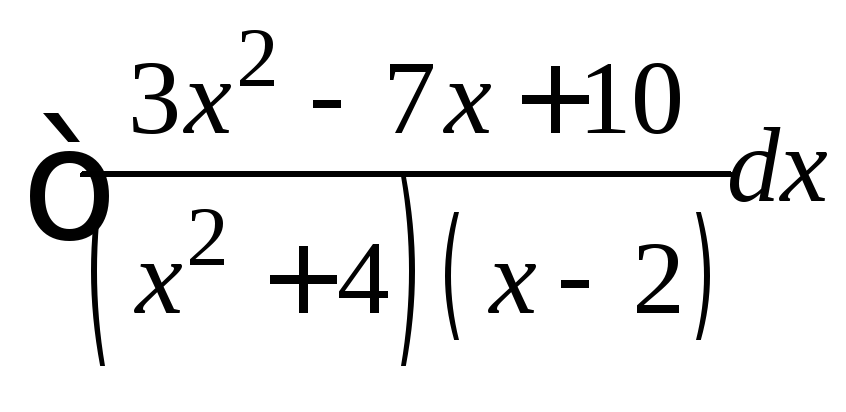Решение. Подынтегральная рациональная дробь является правильной и разлагается на элементарные дроби вида (4):

.

Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов :

.

Составим систему трех уравнений с тремя неизвестными. Одно уравнение получим, полагая х=2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, например ипри:

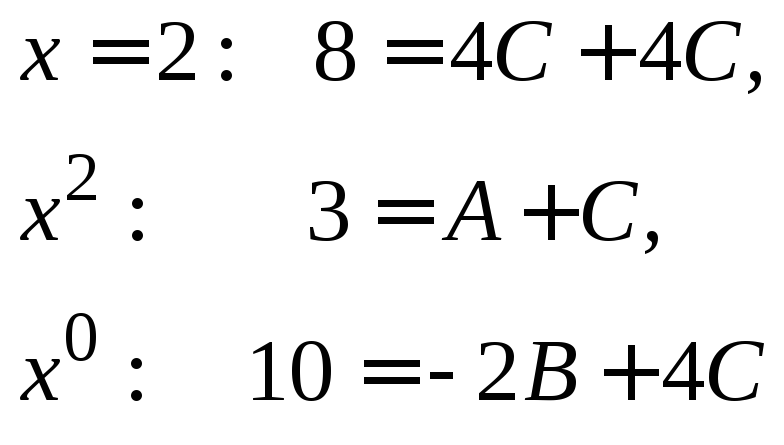
Решение этой системы дает: . Таким образом,

.

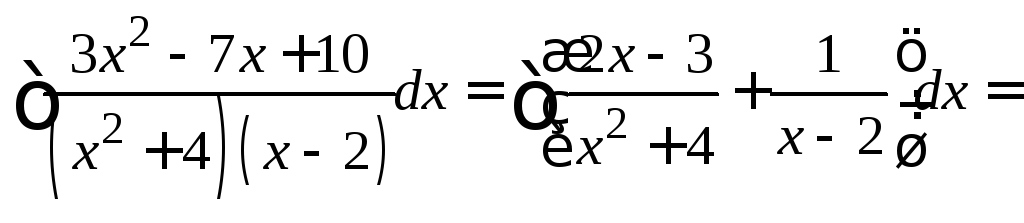
Пример 5. Вычислить определенный интеграл .

Решение. Применим метод замены переменной; положим , откуда. Найдем пределы интегрирования по переменойt: при имеем, а приимеем. Переходя в исходном интеграле к новой переменнойи применяя формулу Ньютона-Лейбница (5), получаем:

.