
- •Дидактический план
- •Литература Основная
- •Дополнительная
- •Перечень умений
- •1.1.2. Векторное произведение
- •1.1.3. Смешанное произведение
- •1.2. Плоскость в пространстве
- •1.2.2. Общее уравнение плоскости. Неполное уравнение
- •1.2.3. Уравнение плоскости «в отрезках»
- •1.2.4. Угол между двумя плоскостями
- •1.2.5. Расстояние от точки до плоскости
- •2. Прямая в пространстве
- •2.1. Различные уравнения прямой
- •2.1.1. Прямая как пересечение двух неколлинеарных плоскостей
- •2.1.2. Угол между двумя прямыми
- •2.2. Прямая и плоскость в пространстве
- •2.3. Типовые задачи
- •3. Поверхности второго порядка
- •3.1. Общее уравнение второго порядка
- •3.2. Канонические уравнения второго порядка
- •3.3. Линейчатые поверхности
- •3.4. Поверхности вращения
- •3.5. Основные поверхности второго порядка
- •3.5.1. Эллипсоид
- •3.5.2. Однополостный гиперболоид
- •3.5.3. Двуполостный гиперболоид
- •3.5.4. Параболоиды
- •3.5.5. Конус
- •3.5.6. Цилиндры второго порядка
- •Приложения
- •1. Понятие линейного пространства
- •2. Понятие линейного функционала
- •3. Гиперплоскость в пространстве Rn
- •4. Уравнение прямой в произвольном линейном пространстве Rn
- •Задания для самостоятельной работы
- •1. Составьте логическую схему базы знаний по теме юниты:
- •2. Решите самостоятельно следующие задачи: Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Тренинг умений
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Пример выполнения упражнения тренинга на умение 1б Задание
- •Решение
- •Выполните самостоятельно следующие задания: Задание 1
- •Глоссарий
О Г Л А В Л Е Н И Е
Стр.
ДИДАКТИЧЕСКИЙ ПЛАН 2
ЛИТЕРАТУРА 3
ПЕРЕЧЕНЬ УМЕНИЙ 4
ТЕМАТИЧЕСКИЙ ОБЗОР 7
1. Плоскость в пространстве 7
1.1. Элементы векторной алгебры 7
1.1.1. Скалярное произведение 7
1.1.2. Векторное произведение 7
1.1.3. Смешанное произведение 8
1.2. Плоскость в пространстве 9
1.2.1. Уравнение плоскости, проходящей через точку M0 (x0,y0,z0) с данным вектором нормали =(A,B,C), 9
1.2.2. Общее уравнение плоскости. Неполное уравнение 10
1.2.3. Уравнение плоскости «в отрезках» 10
1.2.4. Угол между двумя плоскостями 11
1.2.5. Расстояние от точки до плоскости 12
2. Прямая в пространстве 12
2.1. Различные уравнения прямой 12
2.1.1. Прямая как пересечение двух неколлинеарных плоскостей 13
2.1.2. Угол между двумя прямыми 14
2.2. Прямая и плоскость в пространстве 15
2.3. Типовые задачи 16
3. Поверхности второго порядка 21
3.1. Общее уравнение второго порядка 21
3.2. Канонические уравнения второго порядка 22
3.3. Линейчатые поверхности 23
3.4. Поверхности вращения 24
3.5. Основные поверхности второго порядка 24
3.5.1. Эллипсоид 24
3.5.2. Однополостный гиперболоид 26
3.5.3. Двуполостный гиперболоид 27
3.5.4. Параболоиды 28
3.5.5. Конус 29
3.5.6. Цилиндры второго порядка 30
ПРИЛОЖЕНИЯ 31
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 35
ТРЕНИНГ УМЕНИЙ 46
ГЛОССАРИЙ 59
Дидактический план
Плоскость в пространстве и ее уравнения. Прямая в пространстве. Различные способы ее задания.
Взаимное расположение двух прямых, двух плоскостей, прямой и плоскости. Типовые задачи.
Поверхности второго порядка, их канонические уравнения. Метод параллельных сечений. Поверхности вращения.
Литература Основная
*1. Керимова Д.Х., Красовская И.А. Элементы векторной алгебры. Аналитическая геометрия на плоскости. – М.: СГУ, 2004.
*2. Ситникова Е.Г. Аналитическая геометрия. Юнита 1. – М.: СГУ, 2004.
Дополнительная
*1. Бакельман И.Я. Аналитическая геометрия и линейная алгебра. – М.: Наука, 1976.
*2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1987.
*3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1984.
*4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1969.
*5. Ефимов Н.В. Квадратичные формы и матрицы. – М.: Наука, 1972.
*6. Каган М.Л., Самохин М.В. Алгебра и геометрия в инженерном вузе. – М.: МГСУ, 1998.
*7. Клетеник Д.В. Сборник задач по аналитической геометрии. – М., 1972.
*8. Красовская И.А., Керимова Д.Х, Математика (курс 3). Юнита 2,3. Линейная алгебра. Часть 1, 2. – М.: СГУ, 2002.
*9. Осмоловский Н.П., Осипов Ю.В., Керимова Д.Х. и др. Конспект лекций по линейной алгебре и аналитической геометрии. – М.: МГСУ, 2000.
*10. Погорелов А.В. Аналитическая геометрия. – М.: Физматгиз, 1968.
11. Привалов И.И. Аналитическая геометрия. – М.: Физматгиз, 1973.
*12. Цубербиллер О.И. Задачи и упражнения по аналитической геометрии. – М.: Физматгиз, 1968.
_________________________
Примечание. Знаком (*) отмечены работы, на основе которых составлен тематический обзор.
Перечень умений
|
№ п/п |
Умение |
Алгоритм |
|
1 |
Точка на плоскости а)
Определить, лежит ли точка
|
1.
В уравнение плоскости подставить
вместо текущих координат x,
y, z
координаты данной точки
2.
Если при этом получится тождество
(верное равен-ство), то точка
|
|
б)
Найти координаты какой-нибудь точки
|
1.
Двум координатам из трех следует
присвоить произвольные значения:
причем, если
2. Подставить выбранную пару координат в уравнение плоскости. 3. Из полученного относительно третьей координаты уравнения, найти значение этой координаты |
|
|
2 |
Найти
вектор
|
1.
Проверить, будут ли векторы
2. Найти векторное произведение
3.
Положить вектор
|
|
3 |
Найти
расстояние d от точки
|
Вычислить расстояние d по формуле
|
|
4 |
Каноническое и параметрическое уравнение прямой а)
Написать каноническое уравне-ние
прямой по двум точкам
|
1. Вычислить координаты вектора
2.
Взять направляющим вектором прямой
3. Написать
каноническое уравнение прямой,
прохо-дящей через точку
|
|
б)
Написать параметрическое урав-нение
прямой, заданной канони-ческим уравнением
|
1.
Обозначить коэффициент пропорциональности
через t (параметр)
2.
Из полученных равенств выразить
координаты
|
|
№ п/п |
Умение |
Алгоритм |
|
5 |
Написать каноническое уравнение прямой, заданной как пересечение двух плоскостей
( |
1.
Найти какую-нибудь точку
Одной
из переменных следует присвоить
произвольное значение (удобно брать
значение равное нулю) и решить систему
из двух уравнений с двумя неизвестными:
если
2. Выписать
координаты векторов нормали
3.
Найти векторное произведение
4. Взять направляющим вектор прямой
5. Написать каноническое уравнение прямой
|
|
6 |
Найти
точку
|
1. Записать параметрические уравнения заданной прямой (см. ум. 4). 2.
Полученные выражения для координат
3. Из последнего уравнения вычислить значение параметра t. 4.
а) если найденное значение t
единственно, то под-ставив его в
параметрическое уравнение прямой,
получим единственную точку пересечения
б) если уравнение для t несовместно, точек Пересе-чения нет, прямая параллельна плоскости; в) если уравнение справедливо при любом t , то прямая лежит на плоскости – точек пересечения множества. Замечание. Фактически здесь описан один из способов решения совместного уравнения плоскости и прямой |
|
№ п/п |
Умение |
Алгоритм |
|
7 |
Определить тип поверхности второго порядка и ее основные параметры по общему уравнению (в уравнении отсутствуют произве-дения координат)
|
1. В
выражениях
2. Выписать
преобразование координат при
параллельном сдвиге системы координат
в «новое» начало
3. Подставить полученные выражения в уравнение записанное в п.1, получить каноническое уравнение поверхности. 4. По каноническому уравнению определить тип поверхности и ее параметры. |
|
8 |
Определить по каноническому уравнению цилиндра второго порядка: а) уравнение его направ-ляющей; б) какой из координатных осей параллельны его образующие. |
1. Уравнение направляющей (в одной из координат-ных плоскостей) совпадает с уравнением цилиндра. 2. Образующие параллельны той координатной оси, «название» которой в уравнении цилиндра отсутствует (например, если отсутствует Z – то оси OZ). 3. Построить чертеж |
ТЕМАТИЧЕСКИЙ ОБЗОР*
1. Плоскость в пространстве
1.1. Элементы векторной алгебры
1.1.1. Скалярное произведение
Определение.
Скалярное произведение двух векторов
![]() и
и
![]() - число, обозначаемое (
- число, обозначаемое (![]() ,
,![]() )
или
)
или
![]()
![]() и вычисляемое по формуле
и вычисляемое по формуле
(![]() ,
,![]() )
=
)
=
![]() •
•![]()
![]() ,
,
где
![]() – длины векторов, φ – угол между
– длины векторов, φ – угол между
![]() и
и
![]() .
.
В координатной
форме скалярное произведение векторов
![]() =(x1,
y1, z1)
и
=(x1,
y1, z1)
и
![]() =(x2,
y2, z2)
вычисляют так:
=(x2,
y2, z2)
вычисляют так:
(![]() ,
,![]() )=х1·x2+y1·y2+z1·z2.
)=х1·x2+y1·y2+z1·z2.
В частности,
скалярный квадрат вектора (![]() ,
,![]() )=
)=![]() .
.
Из определения скалярного произведения для ненулевых векторов следует, что

Отсюда следует,
что векторы
![]() и
и
![]() ортогональны (
ортогональны (![]() )
тогда и только тогда, когда их скалярное
произведение равно нулю:
)
тогда и только тогда, когда их скалярное
произведение равно нулю:
![]() .
.

 .
.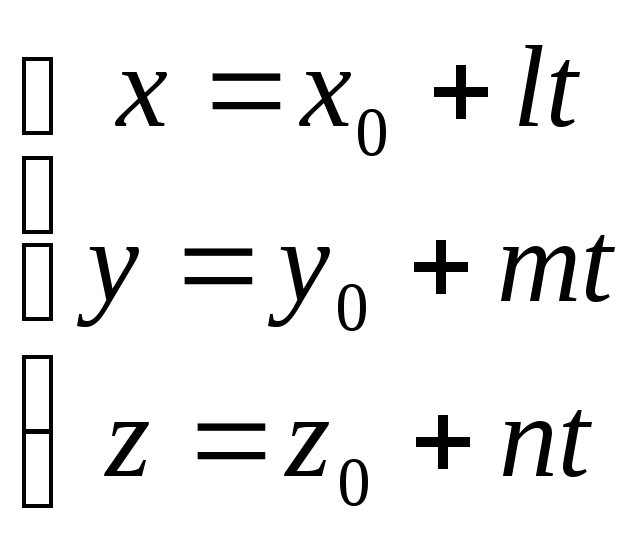

 выделить полные квадраты и записать
исходное уравнение в виде:
выделить полные квадраты и записать
исходное уравнение в виде:
 .
.