6.5. Непрерывность функции и точки разрыва. Краткая теория

1.Функцияназываетсянепрерывной в точкеx₀, если она удовлетворяет следующим условиям: 1) определена в точкеx₀; 2) имеет конечный предел прих→x_0;

3) этот предел равен значению функции в этой точке: (6.1)

(первое определение).

2. Функцияназываетсянепрерывной в точкеx₀, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:(6.2)

(второе определение).

3. Если функцииинепрерывны в точке, то их сумма, произведение и частное (при условии, что знаменатель отличен от нуля) являются функциями, непрерывными в этой точке.

4.Если функцияу=непрерывна в точкеu₀=, а функцияu=непрерывна в точкеx₀, то сложная функция у =непрерывна в точкеx₀.

5.Функция называетсянепрерывнойна некотором промежутке, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны во всех точках, где они определены.

6.Если не выполнено определение непрерывности (6.1) или (6.2), то функция в точкеx₀терпит разрыв, причем:

а) если хотя бы один из односторонних пределов или

бесконечен, то x₀-точка разрыва второго рода;

б) если оба односторонних предела иконечны, но не равны между собой, тоx₀— точка неустранимого разрыва первого рода;

в) если оба односторонних предела иконечны, равны между собой, но не равны, тоx₀— точка устранимого разрыва первого рода.

6.168. Исследовать на непрерывность функции у =в точкех = 1. В случае разрыва установить его характер в точкех= 1:

а) ; б); в); г).

Решение: а) При х = 1 функция не определена, следовательно, функция в точке

х= 1 терпит разрыв (рис. 6.1):, т.е. конечный предел существует; следовательно,х= 1 — точка устранимого разрыва первого рода. (Доопределив функцию в точкех= 1, т.е. положив= 0, получим, что новая функция

будет уже непрерывна в точке х = 1 .)

6) При x= 1 функция не определена, следовательно, функция в точкеx= 1 терпит разрыв (рис. 6.2):

Так как односторонние пределы (достаточно было бы одного) бесконечны, то х= 1 – точка разрыва функции второго рода.

в) При х= 1 функция определена,(x-1) = 0,(x-1) = 0,у(1) = 1 - 1 = 0, т.е.у(х)=у(х) =у(1) = 0, следовательно, функция в точкех= 1 непрерывна

(рис. 6.3).

г) При х= 1 функция определена,у(1)=0,

у(х)=(х+1)=2,у(х)=(х-1)=0,

имеему(х) ≠у(х), таким образом, в точкех = 1 функция терпит неустранимый разрыв первого рода (рис. 6.4.)

Глава 7. Производная

7.1. Определение производной Краткая теория

1.Производной функции называется конечный предел приращения функции к приращению независимой переменной при стремлении последнего к нулю (при условии, что этот предел существует):

.(7.1)

Если функция в точке (или на промежутке) имеет конечную производную, то функция называетсядифференцируемойв этой точке (или на промежутке).

2.Если функция дифференцируема в точке ,(или на промежутке), то она в этой точке непрерывна (или на промежутке). Если функция непрерывна в данной точке, то она обязательно дифференцируема в данной точке.

1. Используя определение производной, найти производную функции.

Решение.Придавая аргументуприращение, найдем соответствующее приращение функции:

.

Составим отношение:

.

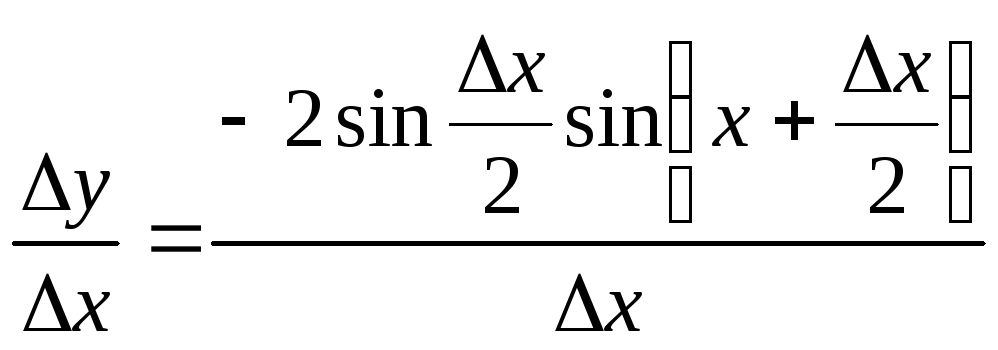Найдем предел этого отношения при :

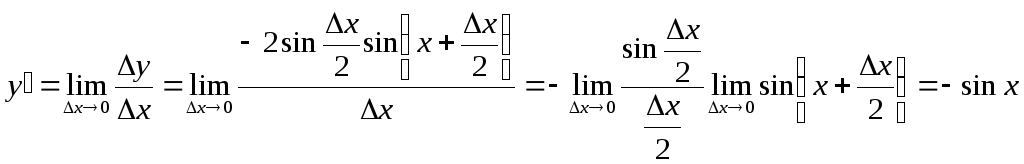
(ибо в силу (6.1) первый предел равен 1).

Таким образом: .

2.Доказать, что функциянепрерывна, но не дифференцируема в точке.

Решение. Функция:

1. определена на всей числовой оси, в том числе в точке ;

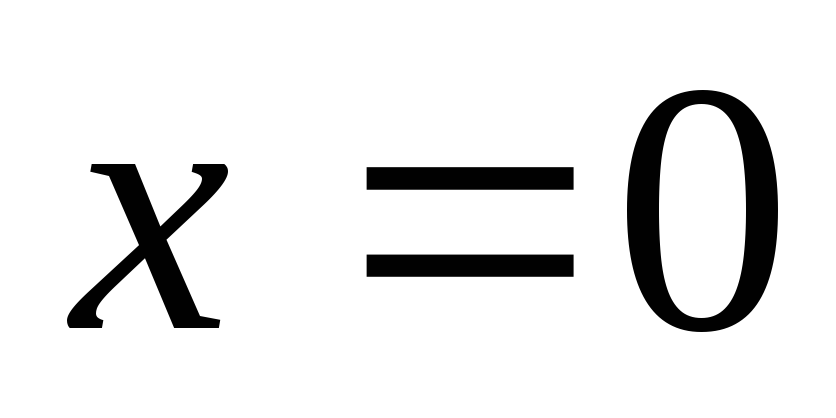2. существует конечный предел ;

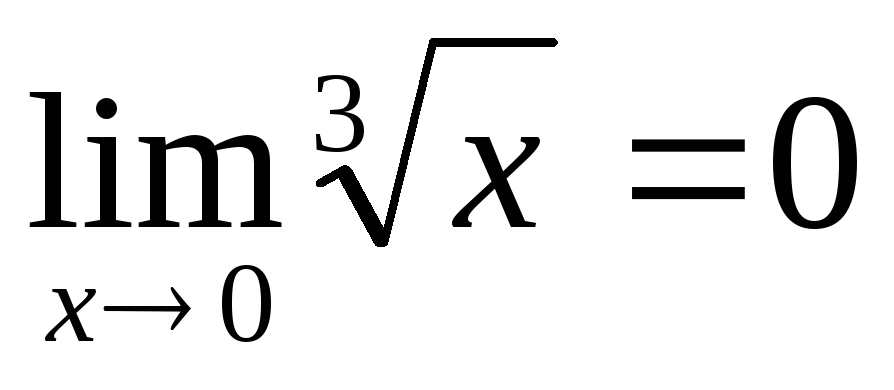3. этот предел равен значению функции в точк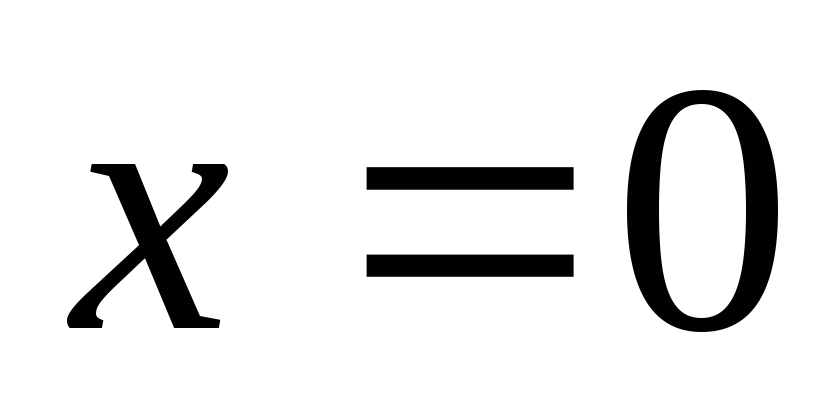е , т.е..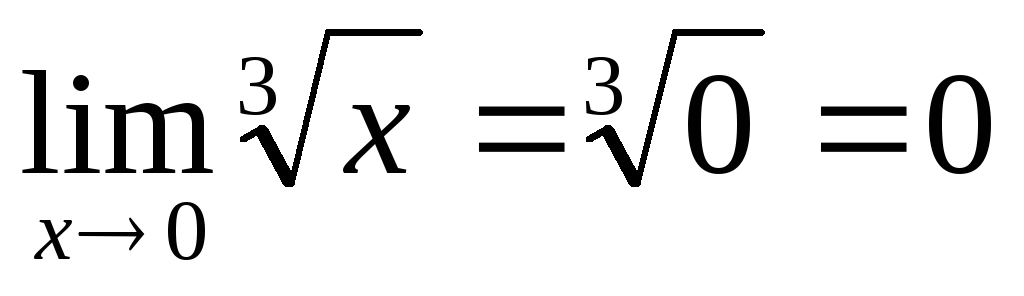

Таким образом, согласно определению (6.4) непрерывности функции в точке, функция непрерывна при .

Производная функции

,

т.е. функция не является дифференцируемой при .

Используя определение производной, найти производные функций:

1..

2..

3..

4..

5..

6..

Доказать, что функции непрерывны и дифференцируемы при :

7.,.

8.,.

Доказать, что функции являются непрерывными, но не дифференцируемы при :

9.,.

10.,.