Теория Информации - Методичка (1 семестр)

Средняя длина кода 5 меньше, чем этот параметр кода 6, следовательно, среди рассмотренных кодов код 5 можно считать наиболее предпочтительным для использования.

Пример 2.5. Пусть необходимо вычислить фактор сжатия и коэффициент сжатия кода 5 из примера 4. Для вычисления фактора и коэффициента сжатия необходимо знать размеры файла до сжатия и после сжатия, однако в условии задачи эти параметры не указаны в явном виде. Предположим, что входной файл, содержит 1000 символов входного алфавита {a, b, c}. Используя уже вычисленное значение средней длины кода, подсчитываем размер закодированного файла 1000 1,3=1300 бит.

Оценим длину исходного файла. Мощность входного алфавита 3, следовательно, для однозначного отображения символов входного алфавита кодовыми словами двоичного алфавита, необходимо использовать не менее двух бит на каждый символ входного алфавита (21<3<22). Например, {a=00, b=01, c=11}. Следовательно, для передачи 1000 символов входного алфавита в двоичном виде необходимо использовать 2000 бит. Таким образом,

коэффициент сжатия =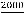=1,53.

В примере 2.2 были даны коды, среди которых надо было найти лучший. В настоящее время существуют алгоритмы, которые гарантированно строят «хорошие» коды для заданного источника данных. В гл. 3 будет рассмотрен пример такого алгоритма.

2.2. Кодовое дерево

Для построения префиксных кодов и описания их свойств удобно использовать так называемое кодовое дерево – граф-дерево с приписанными его ребрам метками из алфавита В. На рис. 2.3 представлен пример двоичного кодового дерева.

Из рис. 2.3 видно, что все ребра дерева помечены элементами двоичного алфавита. Листья дерева задают кодовые слова. Так как из корня дерева к любому листу можно добраться единственным

39

образом, то каждому листу соответствует единственное кодовое слово. Кодовым словом является список меток ребер дерева, которые надо пройти, чтобы добраться от вершины дерева к листу. Так, на рис. 2.3 выделен путь к одному из листьев, задающему кодовое слово 1011.

Уровень

0

1

2

3

4

Рис. 2.3. Пример двоичного кодового дерева

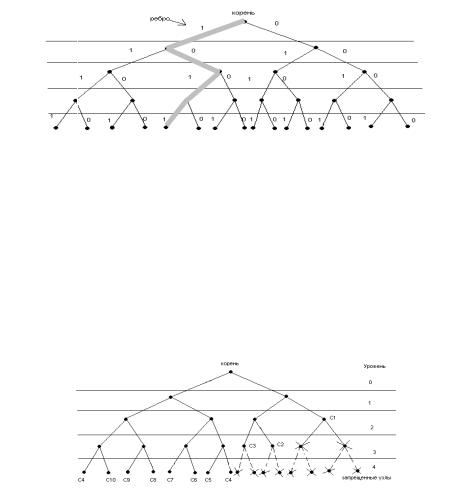
На рис. 2.4 представлено двоичное дерево, очевидно, что можно построить кодовое дерево для алфавита любой мощности. Перечислим основные свойства кодового дерева, построенного для алфавита мощностью D. Во-первых, кодовая конструкция соответствует префиксному коду, так как кодовые слова определяются листьями (конечными узлами). Во-вторых, на i-м уровне существует максимум Di узлов i-го уровня (порядка). В-третьих, каждый узел i- го порядка порождает точно Dn–i узлов n-го уровня.

Рис. 2.4. Пример кодовой конструкции

40

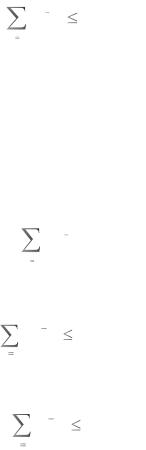
2.3. Неравенство Крафта и утверждение Мак-Миллана

Теорема о неравенстве Крафта. Для существования одно-

значно декодируемого префиксного D-ичного кода, содержащего k кодовых слов с длинами n1, n2, …, nr (ni – натуральные числа) необходимо и достаточно, чтобы выполнялось неравенство Крафта:

k

D nk 1.

k 1

Для доказательства этого утверждения воспользуемся кодовой конструкцией (см., например, рис. 2.2 или 2.3). В качестве кодовых слов будем рассматривать вершины (листья) кодового дерева.

Для простоты упорядочим длины кодовых слов:

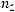
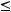
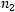
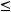
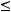
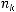
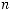. (2.1)

Начнем доказательство с необходимости. Кодовое слово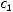

длиной запрещает в точности Dn n1 возможных конечных узлов на последнем 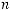-м уровне. Так как слова префиксного кода не объединяются, то на 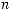-м уровне получаем:

k

Dn nk

k 1

запрещенных узлов. Общее число возможных узлов на 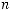-м уровне

равно Dn , следовательно:

k

Dn nk Dn .

k 1

Разделим обе части неравенства на Dn и получим неравенство Крафта:

k

k 1

Для доказательства достаточности покажем, что из справедливости неравенства (2.2) вытекает существование кода с задан-

41

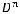
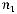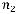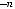
ным набором длин кодовых слов. По-прежнему будем считать, что выполняется равенство (2.1). Из общего числа вершин на ярусе дерева выберем одну любую вершину, сделаем ее концевой (листом дерева). Продолжим строить дерево из оставшихся вершин до следующего яруса . Из общего числа возможных вершин нужно исключить вершин, которые не будут построены, так как одна из вершин на ярусе 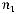была закреплена за кодовым словом и не будет иметь продолжения в кодовой конструкции. На ярусе 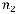останется

вершин. Вновь сделаем одну из вершин этого яруса концевой, тогда на следующем ярусе останется

вершин. Продолжая построение, получаем на последнем nk-м уровне

.

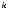
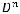
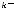
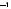
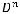
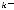
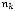
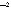
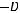
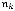
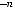
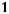Таким образом, мы завершаем построение префиксного кода, сохраняя неравенство Крафта выполненным.

Требование префиксности накладывает ограничения на длины кодовых слов и не позволяет делать длины слов слишком короткими. Так, если в конструкции на рис. 2.3 сделать одно кодовое слово длиной 1, то для того, чтобы в коде попрежнему существовало 11 слов, необходимо увеличить длины оставшихся слов.

При доказательстве неравенства Крафта были использованы особенности префиксных кодов. Очевидно, что было бы удобно иметь условие однозначности декодирования для любого кода и такое условие существует. Рассмотрим его далее.

Теорема об утверждении Мак-Миллана. Каждый однознач-

но декодируемый код удовлетворяет неравенству Крафта. (Без доказательства).

Неравенство Крафта часто называют неравенством Крафта–Мак-Миллана. Считается, что впервые оно было выведено Леоном Крафтом в 1949 г., однако он рассматривал только префиксные коды, а в 1956 г. Броквэй Мак-Миллан доказал необходимость и достаточность этого неравенства для более общего класса однозначно декодируемых кодов.

42

2.4. Теоремы кодирования источников

Сформулируем основные теоремы кодирования источников.

Прямая теорема кодирования источников. Для любого дис-

кретного источника без памяти с конечным алфавитом X={x1, …, xn},

Замечание. В литературе встречается и другая запись выражения (2.3), а именно:

Нормирование энтропии на логарифм от основания кода подчеркивает тот факт, что при вычислении энтропии в числителе правой части неравенства используется логарифм по основанию, совпадающему со значением D.

Доказательство.

Используем неравенство Крафта в следующем виде:

Пока неравенство Крафта выполняется, мы свободны в выборе длин кодовых слов Выберем для каждого слагаемого такое наименьшее значение 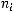при котором будет справедливо неравенство:

(2.4)

При таком ограничении на длины кодовых слов неравенство Крафта будет выполняться, следовательно, можно построить пре-

Далее, используя свойства логарифма, получаем:

43

Просуммируем по всем i :

.

Разделив далее обе части неравенства на 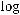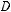и переставив элементы неравенства с умножением на минус 1, получим искомое неравенство.

Обратная теорема кодирования источников. Для однознач-

но декодируемого кода, дискретного источника без памяти с конечным алфавитом X={x1, …, xn}, соответствующими вероятностями появления символов {р(x1), …, р(xn)} и энтропией H(X) средняя длина кодовых слов удовлетворяет условию:

(2.5)

Замечание. Аналогично (2.3) выражение (2.5) может быть записано в виде:

Доказательство.

Запишем неравенство иначе:

Раскроем это выражение.

Используем известную логарифмическую оценку

При обсуждении рассмотренных неравенства Крафта и теоремы кодирования часто упоминают понятие оптимального кода.

44

Однозначно декодируемый код C называется оптимальным, если его средняя длина минимальна в множестве всех кодов, построенных для данного источника.

Другими словами, оптимальное кодирование дает максимальное уплотнение данных, максимальное сжатие. Теоремы кодирования источников показывают, что даже в случае самого лучшего кода средняя длина кода не может быть меньше энтропии источника сообщений. И при этом

длина слов хорошего кода не отличается от энтропии источника более чем на единицу.

Из этих теорем следует, что невозможно закодировать сообщение таким образом, чтобы средняя длина кодовых слов была меньше энтропии сообщения. Кроме того, существует кодирование, при котором средняя длина кодового слова незначительно отличается от энтропии источника сообщений. В некоторых литературных источниках эти теоремы объединяют в одну примерно со следующей формулировкой.

Теорема Шеннона о кодировании источников. Существует способ сжатия любого файла, заданного над алфавитом Х с частотными характеристиками {р1, …, рn}, который обеспечивает сжатие, сколь угодно близкое к Н(Х) бит на символ и не существует способа сжатия файлов с данными частотными характеристиками, обеспечивающего лучшее сжатие.

Краткие итоги

Сжатие позволяет минимизировать технические затраты на передачу и хранение данных.

У кодов сжатия выделяют ряд свойств.

Неравенство Крафта и утверждение Мак-Миллана дают необходимое и достаточное условие существования разделимых и префиксных кодов, обладающих заданным набором длин кодовых слов.

Прямая и обратная теоремы кодирования устанавливают связь средней длины кодового слова и энтропии однозначно декодируемых кодов.

45

Рекомендуемая литература

1.Вернер М. Основы кодирования / М. Вернер. – М.: Тех-

носфера, 2004. – 288 с.

2.Духин А.А. Теория информации / А.А. Духин. – М.: Ге-

лиос АРВ, 2007. – 248 с.

3.Кудряшов Б.Д. Теория информации / Б.Д. Кудряшов. –

СПб.: Питер, 2009. –320 с.

Набор для практики по теме «Теоремы кодирования источников»

Проверьте уровень освоения материала по теме «Теоремы кодирования источников», используя предложенные упражнения и тесты.

Упражнения

1.Для источника без памяти Х с конечным алфавитом {a;b;c;d} и вероятностями появления символов p(a)=0,12; p(b)=0,3; p(c)=0,38; p(d)=0,2 построили двоичный код, средняя длина кодовых слов которого составляет 1,88. Может ли данный код быть префиксным? Обоснуйте ответ.

2.Для источника без памяти Х с конечным алфавитом {a;b;c;d} и вероятностями появления символов p(a)=0,12; p(b)=0,3; p(c)=0,38; p(d)=0,2 построили двоичный код, средняя длина кодовых слов которого составляет 1,40. Может ли данный код быть префиксным? Обоснуйте ответ.

3.Возможно ли существование однозначно декодируемого бинарного кода, содержащего 5 кодовых слов с длинами а) 2,2,4,5,9; б) 3,3,4,4,7? Обоснуйте ответ с теоретической точки зрения.

4.Обоснуйте теоретически, возможно ли существование однозначно декодируемого тернарного кода, содержащего 5 кодо-

вых слов с длинами а) 1,2,3,4,5; б) 3,3,4,4,7?

46

5. Для заданного алфавита построены два кода

Вычислите среднее число бит на символ. Будет ли это значение меньше, больше или равно энтропии? Являются ли данные коды префиксными? Укажите достоинства и недостатки указанных кодов.

Тесты

Вариант 1

1. Буквы алфавита мощностью 4 обозначаются двоичными кодовыми словами: с1=0, с2=10, с3=110, с4=010? Вычислите среднюю длину кодовых слов, при условии равновероятного появления букв

2. Дан трехсимвольный алфавит со следующими вероятностями появления символов: р(а)=0,73; р(в)=0,25; р(с)=0,02. Для данного алфавита построены следующие шесть вариантов кодов:

3. Выберите верные характеристики кода, заданного множеством кодовых слов {0, 10, 101, 110}.

47

4. Выберите верное утверждение о том, между какими величинами устанавливают связь теоремы кодирования источников.

Вариант 2

1. Дан трехсимвольный алфавит со следующими вероятностями появления символов: р(а)=0,73; р(b)=0,25; р(с)=0,02. Для данного алфавита построен следующий код: 1, 00, 01. Чему равна средняя длина кодовых слов?

а) 1/3; б) 1,27; в) 0,423; г) 1,29.

2. Дан трехсимвольный алфавит со следующими вероятностями появления символов: р(а)=0,73; р(b)=0,25; р(с)=0,02. Для данного алфавита построены следующие шесть вариантов кодов:

Какие из этих кодов обладают свойством мгновенной деко-

3. Выберите верные характеристики кода, заданного множеством кодовых слов {01, 10, 00, 11}.

48