§ 3. Евклидовы пространства

1. Скалярное произведение

В курсе аналитической геометрии вводится понятие скалярного произведения двух векторов (на плоскости или в пространстве), которое обладает четырьмя основными свойствами. Мы рассмотрим векторные пространства произвольной природы, для элементов которых каким-либо способом (причем, безразлично каким) определено правило, ставящее в соответствие любым двум элементам число, называемое скалярным произведением этих элементов. При этом важно только, чтобы это правило обладало теми же четырьмя свойствами, что и правило составления скалярного произведения для геометрических векторов на плоскости или в пространстве. Векторные пространства, в которых определено указанное правило, называются евклидовыми пространствами.

Вещественное линейное пространство называется вещественнымевклидовым пространством(или просто евклидовым пространством), если выполнены следующие два требования:

а) Имеется правило, посредством которого любым двум элементам этого пространства иставится в соответствие вещественное число, называемоескалярным произведениемэтих элементов (и обозначаемое символом).

б) Указанное правило подчинено следующим четырем аксиомам:

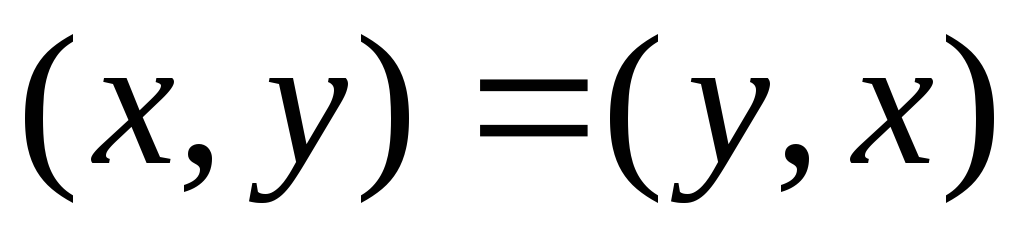1. (коммутативность или симметрия);

2. (дистрибутивность скалярного произведения относительно сложения);

3. ;

4. , если;, если.

Пример

Рассмотрим векторные пространства иливекторов на плоскости или в пространстве. Скалярное произведение любых двух векторов определим стандартным образом (как произведение длин этих векторов на косинус угла между ними). В курсе аналитической геометрии доказывается, что в этом случае выполняются аксиомы 1) – 4). Следовательно, пространстваиявляются евклидовыми пространствами.

Утверждение

Арифметическое пространство Rⁿ, в котором скалярное произведение векторов задано равенством

,

является евклидовым пространством. Оно обозначается Eⁿ.

Пример(неравенство Коши-Буняковского)

Для любых двух элементов иевклидова пространства справедливо неравенство

,

называемое неравенством Коши–Буняковского.

►Для любого вещественного числа в силу аксиомы (4) скалярного произведения справедливо неравенство

.

В силу аксиом (1) – (3) последнее неравенство можно переписать в виде

.

Необходимым и достаточным условием неотрицательности последнего квадратного трехчлена является неположительность его дискриминанта :

.

Из неравенства сразу же следует неравенство Коши–Буняковского.

В том случае, когда квадратный трехчленвырождается в линейную функцию. Но в этом случае элементявляется нулевым, так что, и неравенствотакже справедливо. ◄

Наша очередная задача – ввести в произвольном евклидовом пространстве понятие нормы (или длины) каждого элемента. Для этого введем понятие нормированного пространства.

Векторное пространство называетсянормированным, если выполнены следующие два требования:

а) Имеется правило, посредством которого каждому элементу ставится в соответствие вещественное число, называемоенормой(илидлиной) указанного элемента и обозначаемое символом.

б) Указанное правило подчинено следующим трем аксиомам:

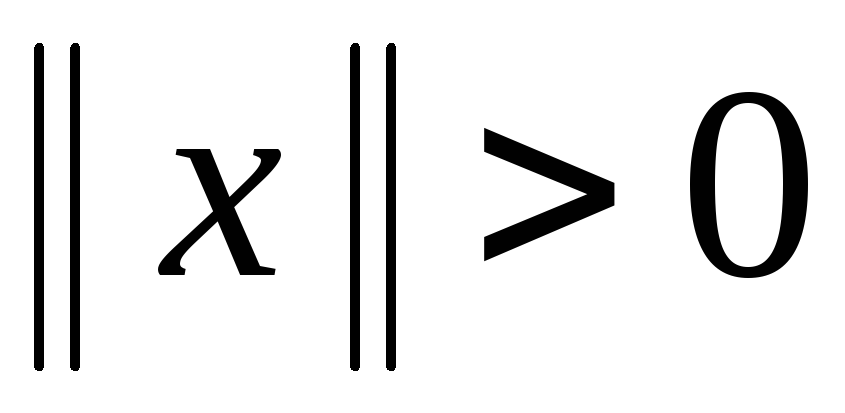1. , если;, если;

2. ,;

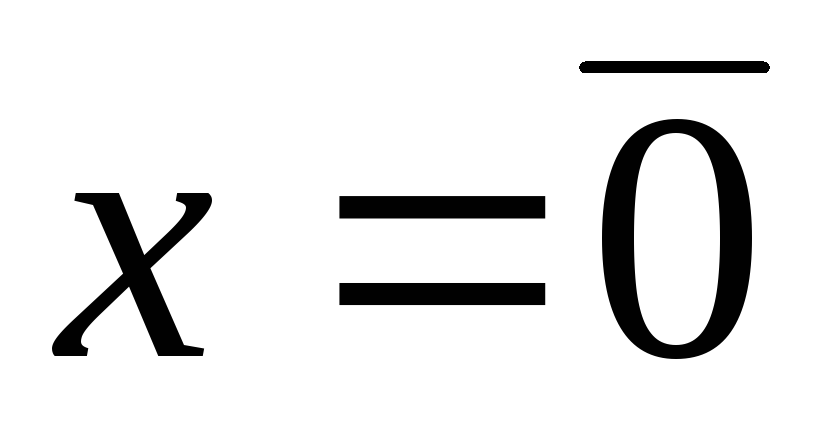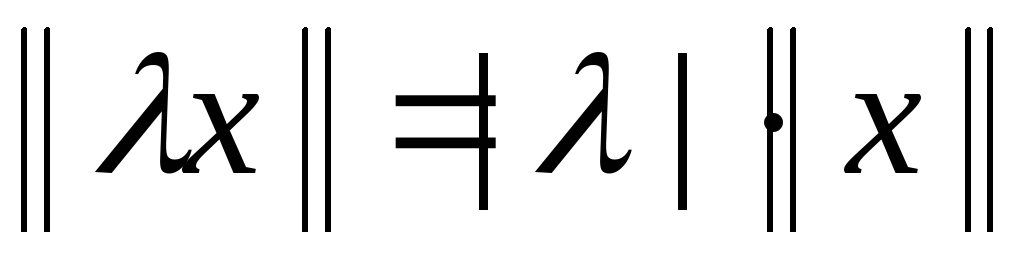
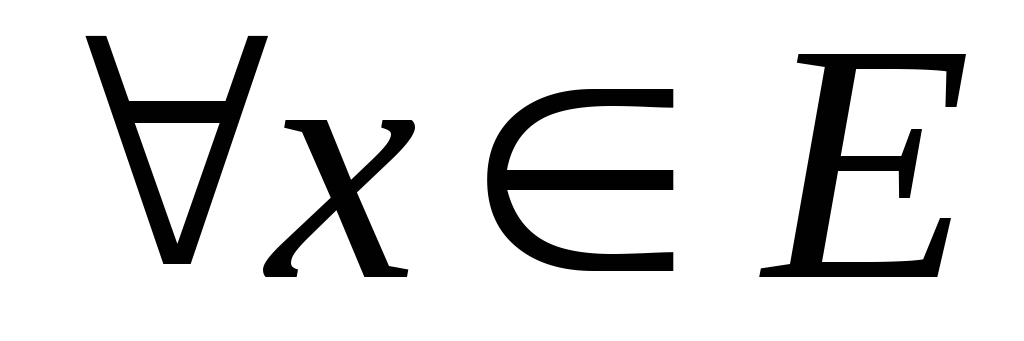
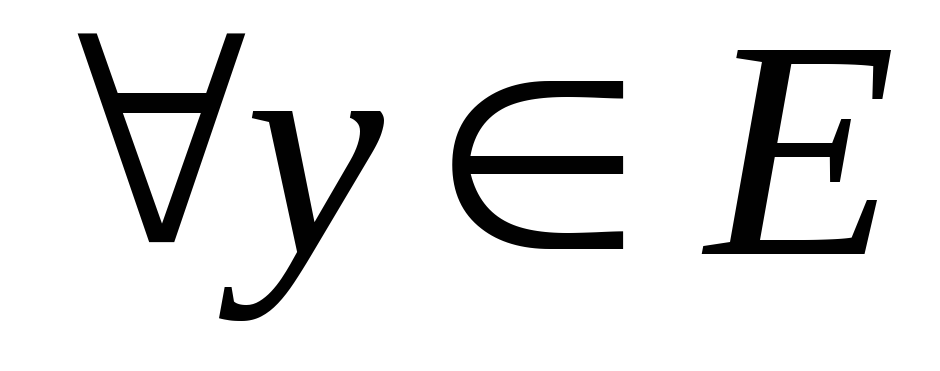
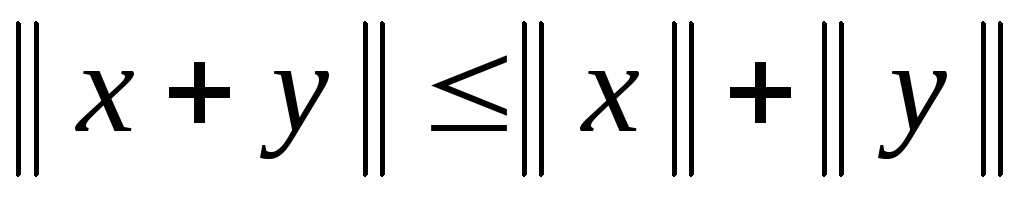3. (неравенство треугольника).

ТЕОРЕМА.Всякое евклидово пространство является нормированным, если в нем норму любого элемента определить равенством

.

В любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными элементами иэтого пространства. Аналогично тому, как это делается в курсе аналитической геометрии (на плоскости и в пространстве), мы назовемуглом между элементамиитот (изменяющийся в пределах отдо) угол, косинус которого определяется соотношением

.

Данное нами определение угла корректно, ибо в силу неравенства Коши-Буняковского дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.

Будем называть два произвольных элемента иевклидова пространстваортогональными, если(в этом случае).

Снова проводя аналогию с геометрическими объектами, назовем сумму двух ортогональных элементовигипотенузойпрямоугольного треугольника, построенного на элементахи.

Во всяком евклидовом пространстве справедлива теоремаПифагора:квадрат гипотенузы равен сумме квадратов катетов. В самом деле, посколькуиортогональны, а, следовательно,, то в силу аксиом и определения нормы

Ранее было введено понятие базиса -мерного векторного пространства. Все базисе в произвольном векторном пространстве являлись равноправными, и у нас не было оснований предпочитать один базис другому. В евклидовом пространстве существуют специальные, особо удобные базисы, называемые ортонормированными базисами. Эти базисы играют ту же роль, что и декартов прямоугольный базис в аналитической геометрии.

Говорят, что элементов-мерного евклидова пространстваобразуютортонормированный базисэтого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если

Для того чтобы установить корректность определения, следует доказать, что входящие в это определение векторы образуют один из базисов-мерного пространства. А для этого (в силу теоремы о связи между понятиями базиса и размерности) достаточно доказать, что эти элементы линейно независимы, т.е. равенство

возможно лишь при .

Докажем это. Пусть – любой из номеров. Умножая данное равенство скалярно на элементи пользуясь аксиомами скалярного произведения и соотношениями ортогональности, мы получим, что.

Ценность понятия ортонормированного базиса была бы невелика, если бы не следующая теорема.

ТЕОРЕМА.Во всяком -мерном евклидовом пространстве существует ортонормированный базис.

Произвольный ортонормированный базис любого евклидова пространства обладает свойствами, аналогичными свойствам декартова прямоугольного базиса. Так, например, в ортонормированном базисе скалярное произведение двух любых векторов равно сумме произведений соответствующих координат этих векторов.

Еще раз подчеркнем, что существенным отличием произвольных векторных пространств от их частного случая, евклидовых пространств, является то, что в векторном пространстве не определены метрические соотношения между его элементами.