
- •Глава 1. Дифференциальное исчисление
- •§1. Понятие функции нескольких переменных
- •2. Предел функции
- •3. Непрерывность функции
- •4. Непрерывность по отдельным переменным
- •§2. Частные производные
- •1. Частные производные первого порядка
- •2. Частные производные высших порядков
- •§3. Полный дифференциал и его применение
- •§4. Дифференцирование сложных функций
- •1. Случай одной независимой переменной
- •2. Случай нескольких независимых переменных
- •§5. Неявные функции и их дифференцирование
- •§6.Экстремум функции многих переменных
- •§7.Наибольшее и наименьшее значения функции многих переменных в замкнутой области
- •2.Условный экстремум функции двух переменных
- •§8. Градиент и производная по направлению
- •§9. Метод наименьших квадратов.
- •Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (4) располагаем в таблице:
- •§10. Теория функций многих переменных и основные зависимости, используемые в экономике 1. Производственная функция
- •II. Вопросы промежуточного контроля
§10. Теория функций многих переменных и основные зависимости, используемые в экономике 1. Производственная функция
Функция, выражающая зависимость объёма производства от величины затраченных ресурсов, называется производственной функцией (ПФ).
Если
![]() ,
то ПФ называетсяодноресурсной.
В ряде случаев ПФ может быть сведена к
зависимости производительности труда
у
(то есть выпуска продукта в расчёте на
одного работника) от капиталовооруженности
труда х
(то есть величины капитала в расчёте на
одного работника), где капиталовооруженность
–
,
то ПФ называетсяодноресурсной.
В ряде случаев ПФ может быть сведена к
зависимости производительности труда
у
(то есть выпуска продукта в расчёте на
одного работника) от капиталовооруженности
труда х
(то есть величины капитала в расчёте на
одного работника), где капиталовооруженность
–
![]() (здесь К – величина капитала,
(здесь К – величина капитала,![]() ─ численность занятых).
─ численность занятых).
Возникновение
теории производственных функций
относится к 1928 году. Тогда появилась
статья американских учёных Д. Кобба и
П. Дугласа, в которой впервые была введена
функция, выражающая зависимость между
объёмом основных фондов К,
затратами труда
![]() и объёмом выпускаемой продукции
и объёмом выпускаемой продукции![]() ,
где
,
где![]() .
График ПФКД в трёхмерном пространстве
есть коническая поверхность (рис.1).
.
График ПФКД в трёхмерном пространстве
есть коническая поверхность (рис.1).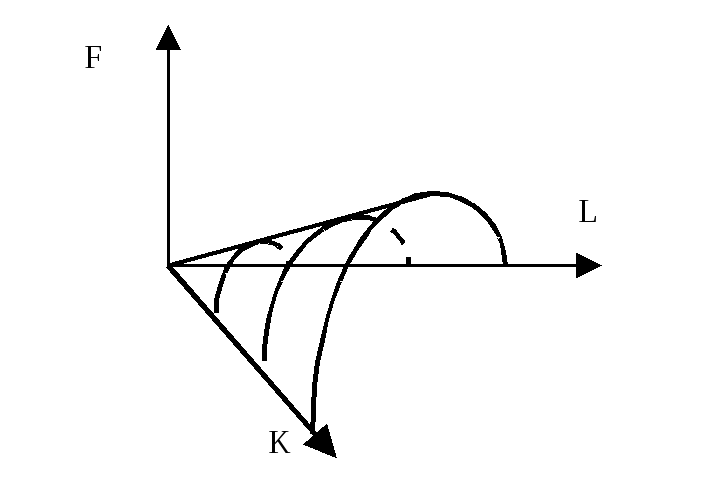 Рис.1
Рис.1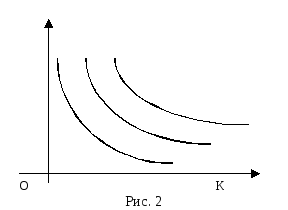
Для
производственной функции двух переменных
![]() линией уровня, соответствующей
линией уровня, соответствующей![]() ,
является множество точек плоскости с
неотрицательными координатами,
удовлетворяющих условию
,
является множество точек плоскости с
неотрицательными координатами,
удовлетворяющих условию![]() .
Для функции Кобба-Дугласа
.
Для функции Кобба-Дугласа![]() линии уровня, соответствующие
линии уровня, соответствующие![]() ,
задаются уравнением
,
задаются уравнением![]() или
или![]() .
Линии уровня функции
.
Линии уровня функции![]() для различных значений
для различных значений![]() изображены на рис. 2.
Точки
изображены на рис. 2.
Точки![]() ,
лежащие на одной линии уровня, соответствуют
различным наборам затрат, обеспечивающим
один и тот же выпуск продукции.
Линии
уровня ПФ называютсяизоквантами.
Отметим, что изокванта, соответствующая
,
лежащие на одной линии уровня, соответствуют
различным наборам затрат, обеспечивающим
один и тот же выпуск продукции.
Линии
уровня ПФ называютсяизоквантами.
Отметим, что изокванта, соответствующая
![]() ,
расположена «северо-восточнее» изокванты,
соответствующей
,
расположена «северо-восточнее» изокванты,
соответствующей![]() .
.
Пример
Найдём изокванты
производственной функции Кобба-Дугласа
![]() .
Изокванта этой функции, соответствующая
значению
.
Изокванта этой функции, соответствующая
значению![]() ,
задана уравнением
,
задана уравнением![]() или
или![]() 2.◄
2.◄
Далее выясним, какую экономическую интерпретацию можно дать частным производным ПФ. Отношение
![]()
показывает, какой
дополнительный выпуск приходится на 1
единицу изменения основных фондов
![]() при постоянных затратах труда
при постоянных затратах труда![]() .
Если существует конечный предел
указанного выше отношения при
.
Если существует конечный предел
указанного выше отношения при![]() ,
то это есть частная производная функции
,
то это есть частная производная функции![]() по переменной
по переменной![]()
![]() .
.
Частная производная
![]() называетсяпредельной
фондоотдачей.
Частная производная
называетсяпредельной
фондоотдачей.
Частная производная
![]() называетсяпредельной
производительностью
труда и определяется аналогично
называетсяпредельной
производительностью
труда и определяется аналогично
![]() .
.
Найдем в явном виде частные производные ПФ
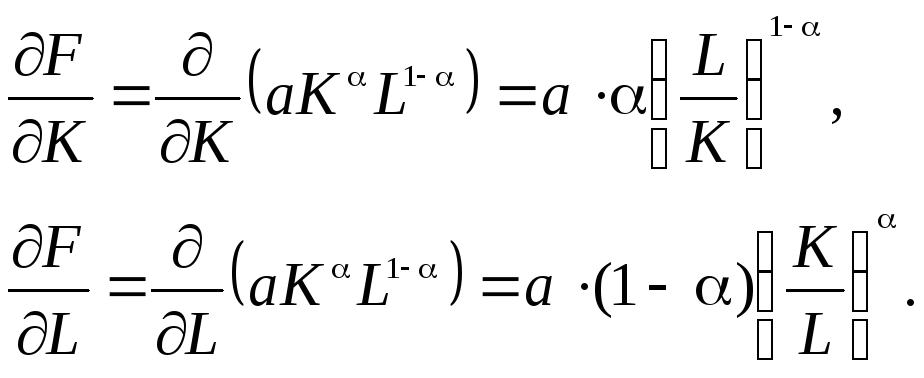
Эластичностью
функции
![]() в точке
в точке![]() по переменной
по переменной
![]() называется
предел
называется
предел![]() ,
по переменной
,
по переменной![]() – предел
– предел
![]() .
Значит
.
Значит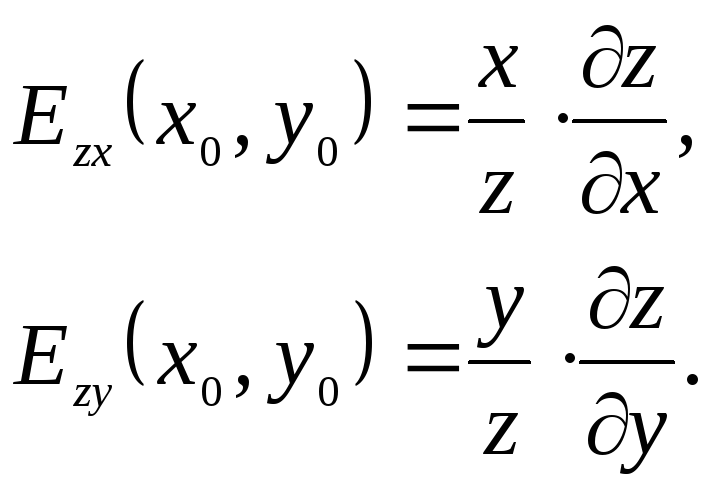 Эластичность приближённо показывает
на сколько процентов изменится выпуск,
если затраты какого-либо одного ресурса
увеличатся на 1 % при неизменных объёмах
другого ресурса.
Эластичность приближённо показывает
на сколько процентов изменится выпуск,
если затраты какого-либо одного ресурса
увеличатся на 1 % при неизменных объёмах
другого ресурса.
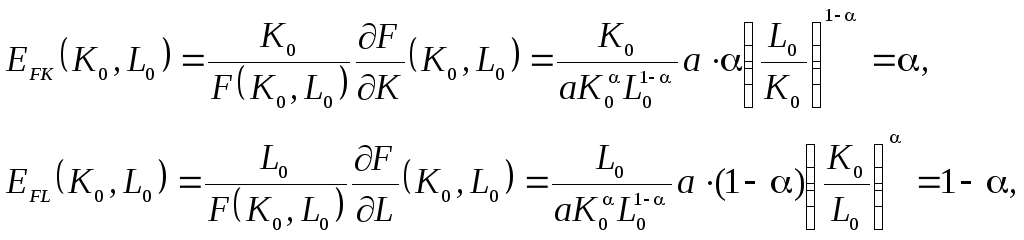
Экономический
смысл параметра
![]() .
Эластичность выпуска по основным фондам
равна
.
Эластичность выпуска по основным фондам
равна![]() .
Значит, относительное изменение основных
фондов
.
Значит, относительное изменение основных
фондов![]() на 1 % вызывает относительное изменение
выпуска на
на 1 % вызывает относительное изменение
выпуска на![]() % (приблизительно), если считать изменение
% (приблизительно), если считать изменение![]() на 1% достаточно малым.
на 1% достаточно малым.
Пример
Функции спроса на
товары
![]() и
и![]() имеют вид:
имеют вид:![]() ;
;![]()
где
![]() ,
,![]() и
и![]() ,
,![]() – спрос на товары
– спрос на товары![]() и
и![]() и их цены соответственно,
и их цены соответственно,
![]() – часть дохода потребителя, которую он
расходует на приобретение названных
товаров. Определить коэффициенты
эластичности функций при
– часть дохода потребителя, которую он
расходует на приобретение названных
товаров. Определить коэффициенты
эластичности функций при
![]() .
.
►
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Величины
![]() и
и
![]() показывают, что с ростом цены товара
показывают, что с ростом цены товара![]() на 1%, спрос на товар
на 1%, спрос на товар![]() снижается на 1,8%, а спрос на товар
снижается на 1,8%, а спрос на товар![]() повышается на 0,043%.
повышается на 0,043%.
Аналогично величины
![]() и
и
![]() Ер2(у)
показывают, что с увеличением цены
товара
Ер2(у)
показывают, что с увеличением цены
товара![]() на 1%, спрос на товар
на 1%, спрос на товар![]() повышается на 0,11%, а спрос на товар
повышается на 0,11%, а спрос на товар![]() снижается 0,27%.◄
снижается 0,27%.◄
Пусть выпуск
![]() является постоянным, (то есть все наборы
затрачиваемых ресурсов расположены на
одной изокванте), тогда полный дифференциал
ПФ
является постоянным, (то есть все наборы
затрачиваемых ресурсов расположены на
одной изокванте), тогда полный дифференциал
ПФ![]() тождественно равен нулю
тождественно равен нулю
![]() ,
здесь
,
здесь
![]() и
и![]() ─ дифференциалы переменных
─ дифференциалы переменных![]() и
и![]() .
.![]() ,
значит,
,
значит,![]() .
.
Отношение
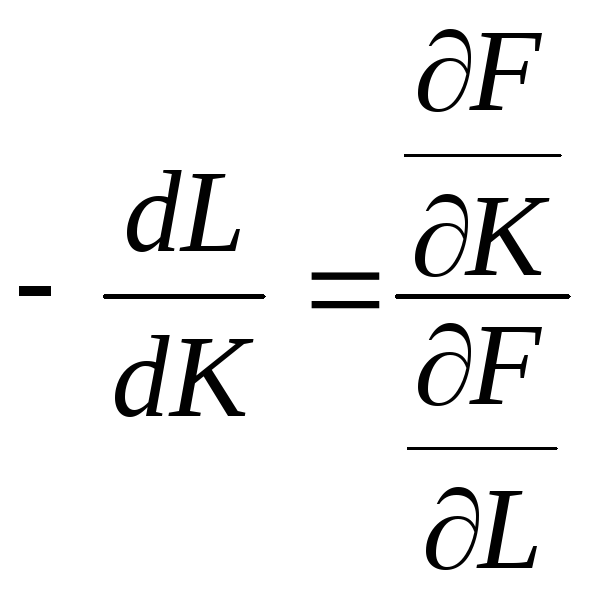 является предельной нормой замены
основного капитала трудом.
является предельной нормой замены
основного капитала трудом.
2. Функция
полезности. Задача потребительского
выбора (ЗПР)
В основе модели поведения потребителей
лежит гипотеза, что каждый из них,
осуществляя выбор наборов благ при
заданных ценах и имеющемся доходе,
стремиться максимизировать уровень
удовлетворения своих потребностей.
Пусть на рынке потребителю предлагается
n
различных наборов благ
![]() где
где![]() -
количествоi-го
блага в натуральных единицах. Блага
приобретаются по рыночным ценам
-
количествоi-го
блага в натуральных единицах. Блага
приобретаются по рыночным ценам
![]() соответственно. Стоимость набора благ
-
соответственно. Стоимость набора благ
-![]() В распоряжении потребителя имеется
ограниченное число денегR
(доход). Ясно, что существует бюджетное
ограничение
В распоряжении потребителя имеется
ограниченное число денегR
(доход). Ясно, что существует бюджетное
ограничение
![]() Полезность блага
– это способность удовлетворять ту или
иную потребность. Потребитель выбирает
наиболее предпочтительный набор среди
всех доступных. В XIX
веке была введена функция полезности
для предпочтения одного набора другому.
Основное ее свойство в том, что потребитель
предпочитает набор X, а не Y, если u(X)>u(Y),
то есть она упорядочивает наборы по
предпочтению.
Полезность блага
– это способность удовлетворять ту или
иную потребность. Потребитель выбирает
наиболее предпочтительный набор среди
всех доступных. В XIX
веке была введена функция полезности
для предпочтения одного набора другому.
Основное ее свойство в том, что потребитель
предпочитает набор X, а не Y, если u(X)>u(Y),
то есть она упорядочивает наборы по
предпочтению.
 Рис.3.
Рассмотрим
пространство двух благ (товаров).
Функция полезности
Рис.3.
Рассмотрим
пространство двух благ (товаров).
Функция полезности
![]() – это субъективная числовая оценка
полезностиu
набора товаров (x,y).
Линии уровня функции полезности называют
кривыми
безразличия.
Так как если
– это субъективная числовая оценка
полезностиu
набора товаров (x,y).
Линии уровня функции полезности называют
кривыми
безразличия.
Так как если
![]() то потребителю безразлично, каким
набором обладать, так как они имеют
одинаковую полезность.
то потребителю безразлично, каким
набором обладать, так как они имеют
одинаковую полезность.
Чем
«северо-восточнее» расположена кривая
безразличия, тем большему уровню она
соответствует (рис.3). Кривые безразличия
являются убывающими.
В теории
потребительского выбора большую роль
играют предельные полезности, которые
выражают дополнительное удовлетворение
от потребления одной дополнительной
единицы блага. Математически этот факт
описывается частными производными
функции полезности:
![]() Предельные полезности положительны,
так как с увеличением потребления блага
его полезность возрастает. Вектор,
координаты которого есть предельные
полезности, называетсявектором
предельных полезностей.
Таким образом
Предельные полезности положительны,
так как с увеличением потребления блага
его полезность возрастает. Вектор,
координаты которого есть предельные
полезности, называетсявектором
предельных полезностей.
Таким образом
![]() .
Закон убывающей полезности гласит, что
с увеличением потребления блага его
предельная полезность убывает, то есть
.
Закон убывающей полезности гласит, что
с увеличением потребления блага его
предельная полезность убывает, то есть![]() Рассмотрим вопрос о взаимозаменяемости
благ. Пусть объемы потребляемых благ
изменились на малые величины
Рассмотрим вопрос о взаимозаменяемости
благ. Пусть объемы потребляемых благ
изменились на малые величины![]() и
и![]() .
Тогда полным приращением полезности
является величина
.
Тогда полным приращением полезности
является величина![]() ,
где
,
где![]()
![]() Если двигаться вдоль линии уровня, то
Если двигаться вдоль линии уровня, то![]() и, следовательно, можно считать равной
нулю и главную линейную часть полного
приращения, то есть
и, следовательно, можно считать равной
нулю и главную линейную часть полного
приращения, то есть![]() .
Тогда
.
Тогда![]() или
или это есть предельная норма замены первого
блага вторым. Она показывает, сколько
надо единиц второго товара, чтобы
заменить выбывшую малую единицу первого.
Если потребитель обладает доходомR,
то множество всех наборов товаров
стоимостью не более R
называется бюджетным
множеством.
Граница бюджетного множества - это
множество наборов, которые стоят ровно
R.
ЗПВ (задача рационального поведения
потребителя на рынке) заключается в
выборе такого набора, который максимизирует
функцию полезности при заданном бюджетном
ограничении, то есть
это есть предельная норма замены первого
блага вторым. Она показывает, сколько
надо единиц второго товара, чтобы
заменить выбывшую малую единицу первого.
Если потребитель обладает доходомR,
то множество всех наборов товаров
стоимостью не более R
называется бюджетным
множеством.
Граница бюджетного множества - это
множество наборов, которые стоят ровно
R.
ЗПВ (задача рационального поведения
потребителя на рынке) заключается в
выборе такого набора, который максимизирует
функцию полезности при заданном бюджетном
ограничении, то есть
![]() Таким образом, на бюджетном множестве
требуется найти точку, принадлежащую
кривой безразличия с максимальным
уровнем полезности. Графически поиск
означает последовательный переход на
линии все более высокого уровня полезности
до тех пор, пока линии еще имеют общие
точки с бюджетным множеством. Следовательно,
искомая точка лежит на границе бюджетного
множества. В ней кривая безразличия
касается линии бюджетного ограничения.
Следовательно, ЗПВ можно заменить
задачей на условный экстремум:
Таким образом, на бюджетном множестве
требуется найти точку, принадлежащую
кривой безразличия с максимальным
уровнем полезности. Графически поиск
означает последовательный переход на
линии все более высокого уровня полезности
до тех пор, пока линии еще имеют общие
точки с бюджетным множеством. Следовательно,
искомая точка лежит на границе бюджетного
множества. В ней кривая безразличия
касается линии бюджетного ограничения.
Следовательно, ЗПВ можно заменить
задачей на условный экстремум:![]() Так как функция полезности является
выпуклой, то на бюджетном множестве
существует единственная точка максимума
функции полезности.
Так как функция полезности является
выпуклой, то на бюджетном множестве
существует единственная точка максимума
функции полезности.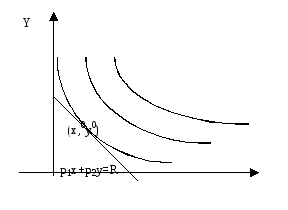 рис.4.
Значит, у потребителя даже нет выбора
в том, как с наибольшей пользой потратить
свои деньги, так как существует
единственный набор
рис.4.
Значит, у потребителя даже нет выбора
в том, как с наибольшей пользой потратить
свои деньги, так как существует
единственный набор
![]() ,
максимизирующий полезность. Эта точка
называетсяточкой
спроса
(рис.4).
Для решения задачи на условный
экстремум построим функцию Лагранжа
,
максимизирующий полезность. Эта точка
называетсяточкой
спроса
(рис.4).
Для решения задачи на условный
экстремум построим функцию Лагранжа
![]() .
Согласно необходимому условию локального
экстремума имеем
.
Согласно необходимому условию локального
экстремума имеем
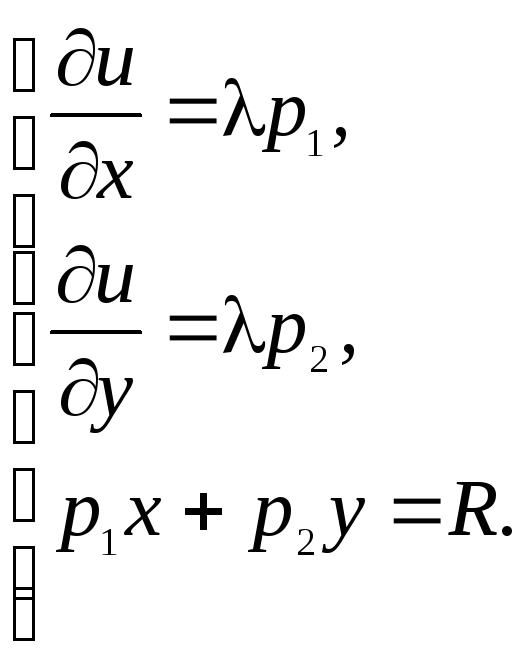
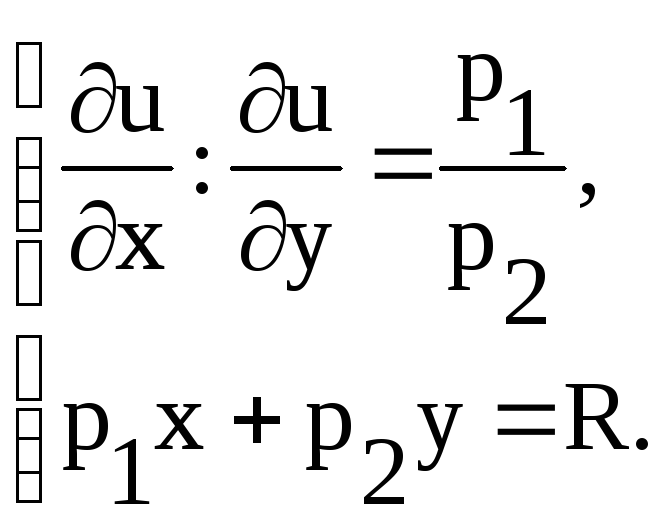 Вывод:
точка спроса лежит на границе бюджетного
множества. В ней вектор предельных
полезностей пропорционален вектору
цен. Координаты и точки спроса есть
функции параметров p1,
p2
и R:
Вывод:
точка спроса лежит на границе бюджетного
множества. В ней вектор предельных
полезностей пропорционален вектору
цен. Координаты и точки спроса есть
функции параметров p1,
p2
и R:
![]() .
.
Полученные функции называются функциями спроса на первый и второй продукты соответственно. Важным свойством является их однородность нулевой степени относительно цен и дохода, то есть пропорциональное изменение цен и дохода не влечет изменение спроса на продукт (первый или второй – безразлично).
Пример
Линии уровня
функции издержек производства называются
изокостами.
Пусть функция полных издержек
двухпродуктовой фирмы задана уравнением
![]() ,
где
,
где![]() и
и
![]() - объемы
выпуска товаров первого и второго видов
соответственно. Найти изокосту (линию
постоянных издержек) для
- объемы
выпуска товаров первого и второго видов
соответственно. Найти изокосту (линию
постоянных издержек) для
![]() и множество производственных
возможностей, ограниченное издержками
производства в объеме 32.
и множество производственных
возможностей, ограниченное издержками
производства в объеме 32.
►Изокоста задается
уравнением
![]() или
или![]() ,
то есть является дугой окружности
радиуса 5 с центром в начале координат.
Множество производственных возможностей
определяется неравенствами:
,
то есть является дугой окружности
радиуса 5 с центром в начале координат.
Множество производственных возможностей
определяется неравенствами:![]() ,
то есть является четвертью круга,
лежащей в первом квадранте.◄
,
то есть является четвертью круга,
лежащей в первом квадранте.◄
Пример
Для некоторого товара определена производственная функция:
![]() ,
где
,
где
![]() и
и![]()
факторы производства. Найти предельную
производительность каждого фактора
при
факторы производства. Найти предельную
производительность каждого фактора
при
![]() .
.
►Находим частные
производные от данной функции по
![]() и
и![]() :
:![]() и
и
![]() .
Искомые
производительности равны:
.
Искомые
производительности равны:
![]() и
и
![]() .◄
.◄
Пример
Фирма производит
товар двух видов в количествах
![]() и
и![]() .
Функция полных издержек определена
соотношением
.
Функция полных издержек определена
соотношением![]() .
Цены этих
товаров на рынке равны
.
Цены этих
товаров на рынке равны
![]() и
и
![]() .
Определить, при каких объемах выпуска
достигается максимальная прибыль и
найти эту прибыль.
.
Определить, при каких объемах выпуска
достигается максимальная прибыль и
найти эту прибыль.
►Функция прибыли имеет вид
![]() .
.
Найдем максимум
этой функции. Вычислим первые частные
производные:
![]() ;
;
![]() и приравняем их нулю. Решив систему,
получим
и приравняем их нулю. Решив систему,
получим
![]() .
Проверим
достаточные условия. Имеем:
.
Проверим
достаточные условия. Имеем:
![]() .
Следовательно, при объемах выпуска
.
Следовательно, при объемах выпуска
![]() достигается максимальная прибыль,
равная
достигается максимальная прибыль,
равная![]() .◄
.◄
Пример
Завод производит
товар двух видов в количестве
![]() и
и![]() .
Известна функция полных издержекC
= 10 + 5
.
Известна функция полных издержекC
= 10 + 5![]() +
7
+
7![]() и функция цен
и функция цен![]() и
и![]() спроса на каждый из этих товаров
спроса на каждый из этих товаров![]() и
и![]() =
19 - 2
=
19 - 2![]()
![]() .
При каких объемах выпуска продукции
достигается максимум прибыли; найти
этот максимум.
.
При каких объемах выпуска продукции
достигается максимум прибыли; найти
этот максимум.
►Функция прибыли I имеет вид
I=![]()
![]() +
+![]()
![]()
![]() =
=![]()
![]() +
+![]()
![]()
![]()
![]() -
-![]() +
+![]() +
+![]()
или
![]() .Найдем
максимум этой функции. Частные производные
.Найдем
максимум этой функции. Частные производные
![]() и
и![]() существуют при любых значениях
существуют при любых значениях![]() и
и![]() .
Чтобы найти точки, в которых они
обращаются в ноль, решим систему
.
Чтобы найти точки, в которых они
обращаются в ноль, решим систему
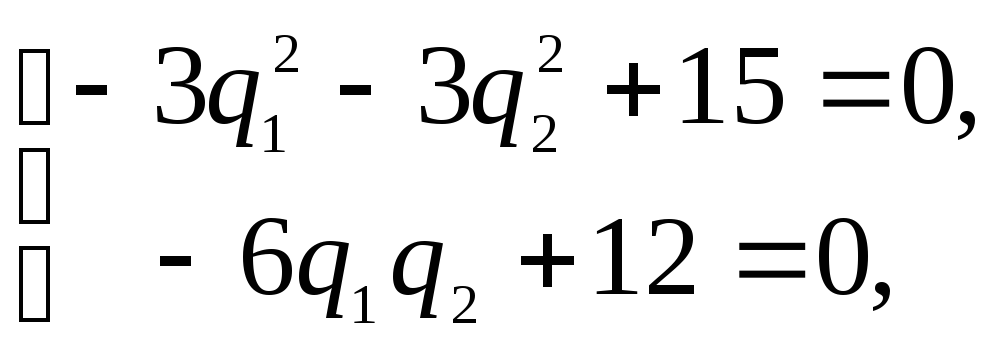
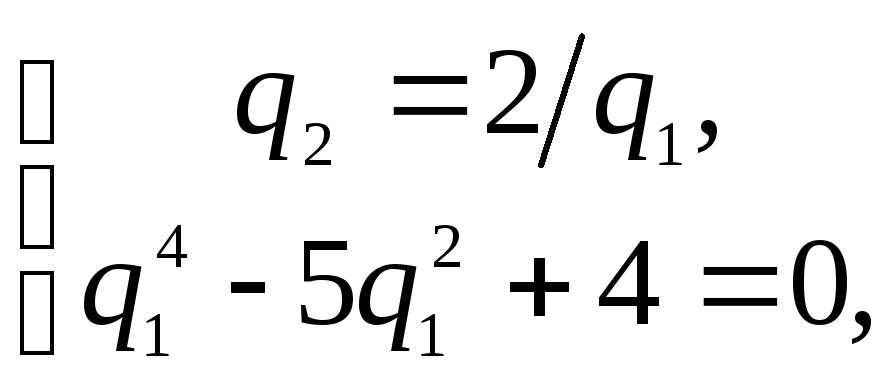
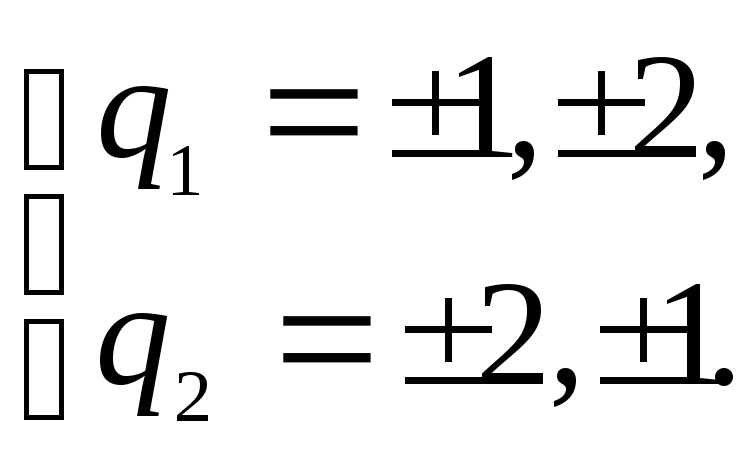 .
.
Отсюда, с учетом
неотрицательности
![]() и
и![]() ,
имеем две стационарные точки
,
имеем две стационарные точки![]() и
и
![]() ,
в которых возможны экстремумы функции
прибыли. Для применения достаточного
признака экстремума вычислим частные
производные второго порядка
,
в которых возможны экстремумы функции
прибыли. Для применения достаточного
признака экстремума вычислим частные
производные второго порядка
![]() ,
,
![]() ,
,![]() .
.
В точке
![]() A=
A=![]() ,B=
,B=![]() ,C=
,C=![]() ,
,
![]() .
Следовательно, в точке M
функция не имеет экстремума.
.
Следовательно, в точке M
функция не имеет экстремума.
В точке
![]() A=
A=![]() ,B=
,B=![]() ,C=
,C=![]() ,
,
![]() .
Следовательно, в точке N
при
.
Следовательно, в точке N
при
![]() и
и![]() функция прибыли имеет максимум
функция прибыли имеет максимум![]() .◄
.◄
Пример
Фирма производит
товар двух видов в количествах
![]() и
и![]() .
Функция полных издержек определена
соотношением
.
Функция полных издержек определена
соотношением![]() .
Цены этих
товаров на рынке равны
.
Цены этих
товаров на рынке равны
![]() и
и
![]() .
Определить, при каких объемах выпуска
достигается максимальная прибыль на
множестве производственных возможностей,
ограниченном издержками производства
в объеме
.
Определить, при каких объемах выпуска
достигается максимальная прибыль на
множестве производственных возможностей,
ограниченном издержками производства
в объеме![]() .
Найти эту прибыль.
.
Найти эту прибыль.
►
![]() .
.
Н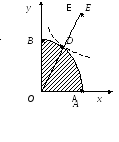 адо
найти максимум этой функции для
неотрицательных
адо
найти максимум этой функции для
неотрицательных![]() и
и![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
т.е. в области,
заданной неравенствами:
,
т.е. в области,
заданной неравенствами:
![]() .
(На рис. эта
область заштрихована).
.
(На рис. эта
область заштрихована).
1)Находим координаты стационарной точки из системы:
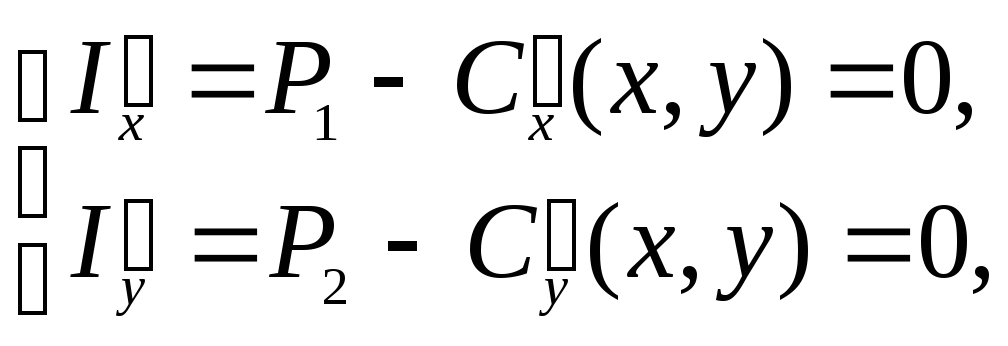
имеющей для данной
задачи вид:
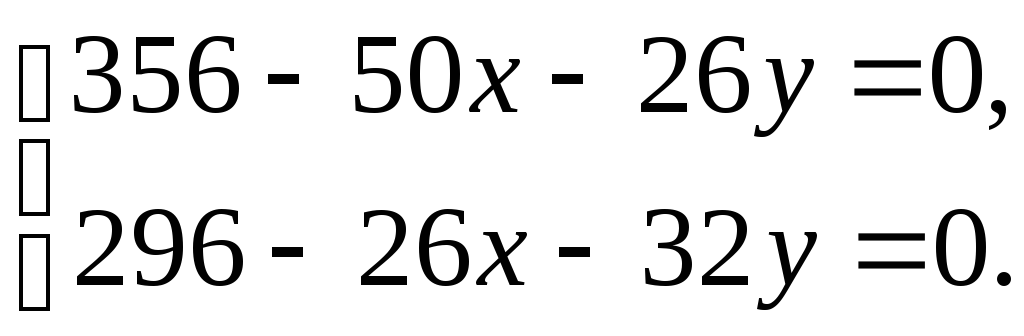 Решив систему, найдем стационарную
точку
Решив систему, найдем стационарную
точку![]() .
Полные издержки
.
Полные издержки
![]() при таких объемах выпуска больше чем
при таких объемах выпуска больше чем
![]() ,
поэтому точка
,
поэтому точка
![]() не принадлежит
множеству производственных возможностей.
не принадлежит
множеству производственных возможностей.
2)Максимум прибыли
достигается, следовательно, на границе
области. Легко проверить, что на отрезках
![]() и
и
![]() критических
точек нет. Найдем критическую точку на
дуге
критических
точек нет. Найдем критическую точку на
дуге
![]() .
Уравнение этой дуги
.
Уравнение этой дуги
![]() .
Составим
функцию Лагранжа:
.
Составим
функцию Лагранжа:
![]()
![]() .
.
Система уравнений для определения координат экстремальной точки имеет вид:
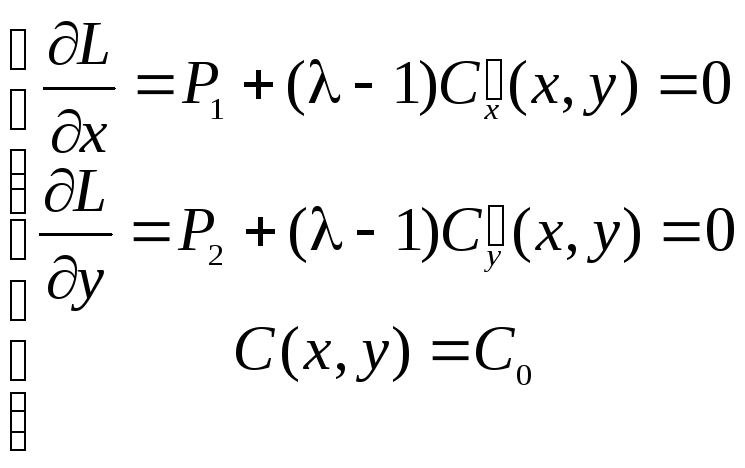 .
.
Исключив
![]() ,
получим систему
,
получим систему
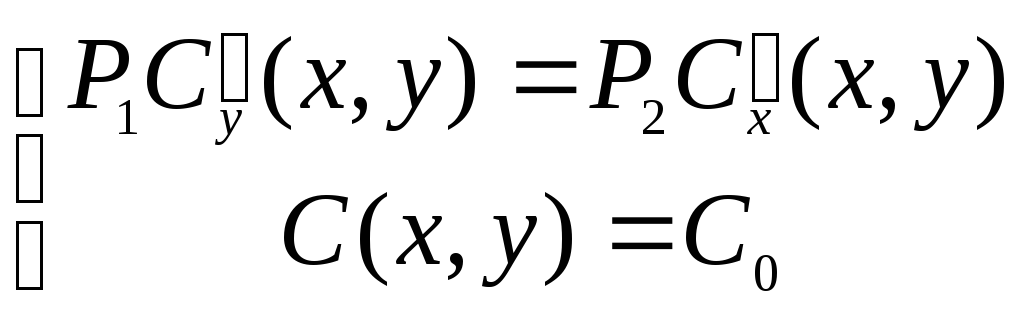 .
Для данной задачи первое уравнение
системы принимает вид:
.
Для данной задачи первое уравнение
системы принимает вид:![]() ,
или
,
или
![]() ,а второе:
,а второе:
![]() .
Решая
систему, найдем экстремальную точку
.
Решая
систему, найдем экстремальную точку
![]() .
В этой точке линия уровня функции
прибыли (эллипс с центром в точке
.
В этой точке линия уровня функции
прибыли (эллипс с центром в точке
![]() касается изокосты
касается изокосты![]() .
.
3) Значения функции
прибыли в угловых точках O(0;
0); A(4;
0) и B(0;
5) меньше чем в точке D(2,
3),
следовательно, при объемах выпуска
![]() достигается
максимальная прибыль
достигается
максимальная прибыль
![]() .◄
.◄
