Основы биомедицинской статистики

В программе Excel доверительные интервалы рассчитываются с помощью функции ДОВЕРИТ (рис.14). Она возвращает значение, с помощью которого можно определить доверительный интервал для математического ожидания генеральной совокупности. Доверительный интервал представляет собой диапазон значений. Выборочное среднее x является серединой этого диапазона, следовательно, доверительный интервал определяется как (x ± ДОВЕРИТ).

Рис. 14. Функция ДОВЕРИТ

ДОВЕРИТ(альфа; станд_откл; размер)

Альфа — это уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется (1 - альфа).100%, или, другими словами, альфа равное 0,05 означает 95процентный уровень надежности.

Станд_откл — это стандартное отклонение (среднее квадратическое отклонение) генеральной совокупности для интервала данных, оно предполагается известным. Размер — это размер выборки.

Автор: доцент Андаспаева А.А.

12

Если какой-либо из аргументов не является числом, то функция ДОВЕРИТ возвращает значение ошибки #ЗНАЧ!.

Если альфа ≤ 0 или альфа ≥ 1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО! Если станд_откл ≤ 0, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Если размер не целое, то оно округляется.

Если размер < 1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Доверительные интервалы для среднего квадратического отклонения.

определяются по следующим формулам, если число испытаний n<100:

где S – среднее квадратическое отклонение. Значения Zн и Zв определяются с помощью табл.4.

При числе испытаний К=n-1 >100 значения Zн и Zв вычисляют по формулам:

где U = t1 при n=∞ – квантиль распределения Стьюдента при доверительной вероятности Рд=0,95.

Доверительные интервалы для коэффициента вариации.

4 Оценка анормальности результатов испытаний

Если результаты измерений можно отнести к нормальному распределению, то грубые погрешности исключают, основываясь на критериях оценки анормальности результатов наблюдений.

Анормальным называют результат измерений, резко отклоняющийся от группы результатов, являющихся нормальными.

План расчета:

1. Полученные результаты ранжируют в порядке возрастания

Х1 < X2 < X3 <... ...< Xn

В программе Excel 2007 расположить результаты в порядке возрастания можно с помощью кнопки на вкладке ДАННЫЕ (рис. 15).

Рис. 15. Сортировка по возрастанию в Excel 2007

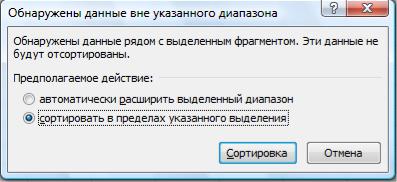
Если предварительно выделить диапазон данных, то появится окно, показанное на рис. 16, в

котором отмечаем точкой СОРТИРОВАТЬ В ПРЕДЕЛАХ УКАЗАННОГО ВЫДЕЛЕНИЯ.

Автор: доцент Андаспаева А.А.

13

Рис. 16. Установка предела сортировки

2. Подсчитывают выборочное среднее, среднее квадратическое отклонение

Чтобы оценить Хn и Х1 в данной нормальной совокупности и принять решение об исключении или оставлении данных значений в составе выборки, находят отклонения этих величин относительно среднего значения, для чего используются следующие формулы:

В программе Excel нет функций, соответствующих данным формулам, поэтому для расчетов их придется набирать в ячейках.

Полученные результаты сравнивают со значением m, взятым из таблиц для данного объема выборки n и принятых уровней значимости q.

Если Un > т или U1 > т , то значения Xn или X1 исключают из дальнейших исследований. Значения т приведены в таблице 5.

Правила оценки анормальности отдельных результатов наблюдений при нормальном распределении результатов изложены в таблице 5.

5 Проверка гипотез о соответствии фактического распределения результатов испытаний теоретическому

Распространять сводные выборочные характеристики на всю партию материала можно с определенной вероятностью, для нахождения которой необходимо знать закон распределения первичных данных. Именно закон распределения дает полную картину варьирования исследуемого свойства, тогда как сводные характеристики, даже генеральные, определяют распределение признака лишь в среднем. Знание закона распределения показателя качества позволяет установить границы между случайными и неслучайными отклонениями сводных выборочных характеристик от нормированного значения (последнее обстоятельство лежит в основе статистического контроля качества продукции).

Многие свойства медицинских и фармацевтических материалов подчиняются нормальному закону распределения, но некоторые из них имеют распределение, отличающееся от нормального. В этом случае вероятность нахождения генеральной характеристики в пределах доверительного интервала снижается или остается неизвестной. Однако следует иметь в виду, что при распределении отдельных результатов измерений, отличающихся от нормального, средние из этих результатов, разде-

Автор: доцент Андаспаева А.А.

14

ленных на группы (выборки), тем ближе следуют нормальному распределению, чем больше численность указанных групп.

М е т о д ы п р о в е р к и с т а т и с т и ч е с к и х г и п о т е з . Исходя из эмпирического распределения полученных экспериментальных данных, на основе их графического изображения или по другим каким-либо соображениям выдвигают гипотезу о соответствии данного эмпирического распределения предполагаемому теоретическому. При сравнении выбранного теоретического распределения с эмпирическим нужно решать вопрос о том, можно ли разницу в этих распределениях считать случайной. Проверяемая гипотеза всегда заключается в предположении чисто случайного характера разницы сравниваемых распределений, т. е. в отсутствии между ними существенных различий. Такую гипотезу часто называют н у л е в о й . Если фактическое различие распределений не достигнет границы, выход за которую при условии правильности нулевой гипотезы маловероятен, то это означает, что нулевая гипотеза при данном исследовании не опровергается. Однако надо четко различать вывод «не опровергается» от вывода «подтверждается». Когда нулевая гипотеза не опровергнута, то те же наблюдения могут оказаться совместимыми и с другими гипотезами, отличающимися от первой. Следовательно, рассматриваемый метод оценки может служить для подтверждения нулевой гипотезы; он может только опровергать, что позволяет делать вывод о существенном, а не случайном различии сравниваемых распределений.

Проверку гипотезы осуществляют с помощью к р и т е р и е в , связывающих те или иные элементы эмпирического распределения элементами теоретического распределения. Малые значения критериев (несогласия) указывают на случайность отклонений сравниваемых распределений, т. е. подтверждают гипотезу их близости или совпадения. Большие значения критериев несогласия ее

риска, на который можно идти, принимая определенные значения критерия за невозможные. Среди уровней значимости чаще используют уровни q = 5% (q = 0,05) и q = 1 % (q=0,01). Чем меньше уровень значимости, тем меньше вероятность забраковать верную гипотезу.

К р и т и ч е с к о й о б л а с т ь ю данного критерия проверки гипотезы называют область тех значений критерия, вероятность попадания в которую при верной гипотезе равна или меньше уровня значимости q.

О б л а с т ь д о п у с т и м ы х з н а ч е н и й критерия лежит вне критической области и является областью тех его значений, вероятность попадания в которую при верной гипотезе равна Р =

1 - q.

Чем больше величина критериев, часто применяемых при проверке близости фактического и теоретического распределений, тем меньше вероятность их получения. Поэтому, если критерий, настолько велик, что вероятность его получения равна или меньше уровня значимости, то значения критериев окажутся в критической области, и это свидетельствует о настолько малой вероятности близости сравниваемых распределений, что практически с риском, равным или меньшим q, можно считать данную близость невероятной; тогда нулевая гипотеза соответствия распределений должна быть отвергнута. Наоборот, если значение критерия будет в области допустимых значений, то оно не противоречит нулевой гипотезе соответствия сравниваемых распределений; поэтому можно принять допустимость нулевой гипотезы, по крайней мере до тех пор, пока более обстоятельное исследование не приведет к противоположному заключению.

5.1Оценка соответствия результатов измерения нормальному закону по величине

асимметрии и эксцесса

Для кривой нормального распределения характерно симметричное расположение отдельных значений относительно среднего, что можно проверить по величине асимметрии, которая является мерой косости.

где К - асимметрия;

Автор: доцент Андаспаева А.А.

15

S - среднее квадратическое отклонение;

Хi – текущее значение результатов испытаний;

Х - среднее значение; n - число испытаний.

К=0 свидетельствует о симметричности кривой распределения. Чем больше К, тем асимметричнее кривая (рис.19).

К>0

К<0

К=0 - кривая нормального распределения, т.е. случайные величины нормально распределены

Рис.17. Асимметрия

В программе Excel асимметрия вычисляется с помощью функции СКОС (рис. 18). Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.

СКОС(число1;число2; ...)

Число1, число2 ...— от 1 до 30 аргументов, для которых вычисляется асимметрия. Можно использовать один массив или одну ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются. Если имеется менее трех точек данных, или стандартное отклонение равно нулю, то функция СКОС возвращает значение ошибки #ДЕЛ/0!.

Рис. 18 Функция СКОС

Автор: доцент Андаспаева А.А.

16

Уравнение для асимметрии в программе Excel определяется следующим образом:

где S — стандартное отклонение выборки.

Эксцесс ( Е ) - позволяет судить о сплющенности (крутости) кривой распределения по сравнению с кривой нормального распределения (рис. 19).

В программе Excel эксцесс вычисляется с помощью функции ЭКСЦЕСС(число1;число2; ...), которая возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением (рис. 19). Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

Е>0

Е=0

Е<0

Рис. 19. Эксцесс

ЭКСЦЕСС(число1;число2; ...)

Число1, число2,...— от 1 до 30 аргументов, для которых вычисляется мода. (Возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных.) Можно использовать один массив или одну ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержа-

щими числа.

Рис. 20 Функция ЭКСЦЕСС

Автор: доцент Андаспаева А.А.

17

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

Если задано менее четырех точек данных или если стандартное отклонение выборки равняется нулю, то функция ЭКСЦЕСС возвращает значение ошибки #ДЕЛ/0!.

В программе Excel эксцесс определяется следующим образом:

6Сравнение двух выборок

6.1Сравнение двух средних независимых выборок (критерий Стьюдента)

Часто в процессе проведения испытаний необходимо сравнить результаты двух независимых выборок с тем, чтобы оценить достоверность разности Х1 – Х2. Если эта разность недостаточно значима, то средние Х1 и Х2 могут относиться к одной и той же генеральной совокупности. Если же эта разность достаточно значима, то средние Х1 и Х2 относятся к разным генеральным совокупностям или к одной совокупности, но при измерении величин Х1 и Х2 имеется достаточная разница в методах их определения.

При большом числе испытаний n>30 и m>30 критерий достоверности определяется по фор-

муле:

S12 S22

n m

где S1, S2 – среднее квадратическое отклонение в первой и второй выборке; n, m – число значений в первой и второй выборке.

Полученное значение сравнивают с табличными значениями критерия Стьюдента. При малом числе испытаний n+m<60

S 2 n 1 1 m 1 2 n m 2

При числе испытаний n=m<30

Автор: доцент Андаспаева А.А.

и по таблице 13 для найденной величины k и при вероятности 95% определяют табличное значение t.

и по таблице 13 для найденной величины k и при вероятности 95% определяют табличное значение t.

В программе Excel применяется функция ТТЕСТ (рис. 21). Она возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ используется, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Рис. 21. Функция ТТЕСТ

ТТЕСТ(массив1;массив2;хвосты;тип)

Массив1 — первое множество данных. Массив2 — второе множество данных.

Хвосты — число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение. Тип — вид исполняемого t-теста.

1Парный

2Двухвыборочный с равными дисперсиями (гомоскедастический)

3Двухвыборочный с неравными дисперсиями (гетероскедастический)

Автор: доцент Андаспаева А.А.

19

Если массив1 и массив2 имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д.

Аргументы хвосты и тип усекаются до целых.

Если хвосты или тип не является числом, то функция ТТЕСТ возвращает значение ошибки

#ЗНАЧ!.

Если хвосты имеет значение, отличное от 1 и 2, то функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!.

TTEСT использует данные массива1 и массива2 для вычисления неотрицательной t- статистики. Если хвосты = 1, TTEСT возвращает вероятность более высокого значения t-статистики, исходя из предположения, что массив1 и массив2 являются выборками, принадлежащими одной и той же генеральной совокупности. Значение, возвращаемое функцией TTEСT в случае, когда хвосты = 2, является двусторонним значением, возвращаемым, когда хвосты = 1 и представляет собой вероятность более высокого абсолютного значения t-статистики, исходя из предположения, что массив1 и массив2 являются выборками, принадлежащими одной и той же генеральной совокупности.

В надстройке АНАЛИЗ ДАННЫХ представлено несколько типов теста для сравнения выборочных средних (рис. 22).

Рис. 22. Пакет анализа

Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Эти три средства допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.

Для всех трех средств, перечисленных ниже, значение t-статистики t вычисляется и отображается как "t-статистика" в выводимой таблице. В зависимости от данных, это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 “P(T <= t) одностороннее” дает вероятность того, что наблюдаемое значение t- статистики будет более отрицательным, чем t. При t >=0 “P(T <= t) одностороннее” делает возможным наблюдение значения t-статистики, которое будет более положительным чем t. “t критическое одностороннее” выдает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного “t критическое одностороннее” равно Alpha.

“P(T <= t) двустороннее” дает вероятность наблюдения значения t-статистики по абсолютному значению большего чем t. “P критическое двустороннее” выдает пороговое значение, так что значение вероятности наблюдения значения t - статистики по абсолютному значению большего “P критическое двустороннее” равно Alpha.

Двухвыборочный t-тест с одинаковыми дисперсиями. Двухвыборочный t-тест Стьюдента служит для проверки гипотезы о равенстве средних для двух выборок. Эта форма t-теста предполагает совпадение значений дисперсии генеральных совокупностей и обычно называется гомоскедастическим t-тестом.

Элементы диалогового окна «Двухвыборочный t-тест с одинаковыми дисперсиями» приведены на рис. 23.

Автор: доцент Андаспаева А.А.

20

Рис. 23. Двухвыборочный t-тест с одинаковыми дисперсиями

Интервал переменной 1. Дается ссылка на первый диапазон анализируемых данных. Диапазон должен состоять из одного столбца или одной строки.

Интервал переменной 2. Дается ссылка на второй диапазон анализируемых данных. Диапазон должен состоять из одного столбца или одной строки.

Гипотетическая средняя разность. Вводится число, равное предполагаемой разности средних. Значение 0 (нуль) указывает, что средние принимаются равными.

Заголовки. Если первая строка или первый столбец входного интервала содержит заголовки, то устанавливается флажок. Флажок снимается, если заголовки отсутствуют; в этом случае подходящие названия для данных выходного диапазона будут созданы автоматически.

Альфа. Вводится уровень надежности для теста. Его значение должно находиться в диапазоне 0...1. Уровень альфа связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы).

Выходной диапазон. Вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

Новый лист. Устанавливается переключатель таким образом, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.

Новая книга. Устанавливается переключатель таким образом, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.

Результаты расчетов выводятся в виде таблицы (табл. 14).

Автор: доцент Андаспаева А.А.