4.5.3 Характеристики оценки измеряемой величины

Задачей измерения является нахождение по полученным наблюдениям наилучшей оценки измеряемой величины  результата измерения и оценки точности этого результата, т.е. степени его близости к истинному значению величины  погрешности измерений. При этом считается, что закон распределения наблюдений и погрешностей известен. Под оценкой в данном случае понимается нахождение значений параметров этих распределений случайных величин по ограниченному числу наблюдений. Полученные оценки параметров распределений являются лишь приближениями к истинным значениям этих параметров и используются в качестве результата измерений и его погрешности. Для того чтобы оценку, получаемую по результатам многократных наблюдений, можно было использовать в качестве параметра функции распределения случайной величины, она должна отвечать ряду требований — быть состоятельной, несмещенной и эффективной.

Состоятельная оценка – это оценка, которая при увеличении числа наблюдений стремится к истинному значению оцениваемого параметра.

Несмещенная оценка - оценка, математическое ожидание которой равно истинному значению оцениваемого параметра.

Эффективная оценка – оценка, имеющая наименьшую дисперсию по сравнению с любой другой оценкой данного параметра.

Методы нахождения оценок параметров распределений, а по ним результатов измерений и их погрешностей зависят от вида функции распределения и от тех соглашений по обработке результатов измерений, которые нормируются в рамках законодательной метрологии в нормативной документации.

4.5.4 Примеры распределения случайных величин

Способы нахождения значений случайной величины зависят от вида функции ее распределения. Однако на практике такие функции, как правило, неизвестны. Если же случайный характер результатов наблюдений обусловлен погрешностями измерений, то полагают, что наблюдения имеют нормальное распределение. Это обусловлено тем, что погрешности измерений складываются из большого числа небольших возмущений, ни одно из которых не является преобладающим. Согласно же центральной предельной теореме сумма бесконечно большого числа взаимно независимых бесконечно малых случайных величин с любыми распределениями имеет нормальное распределение. Нормальное распределение для с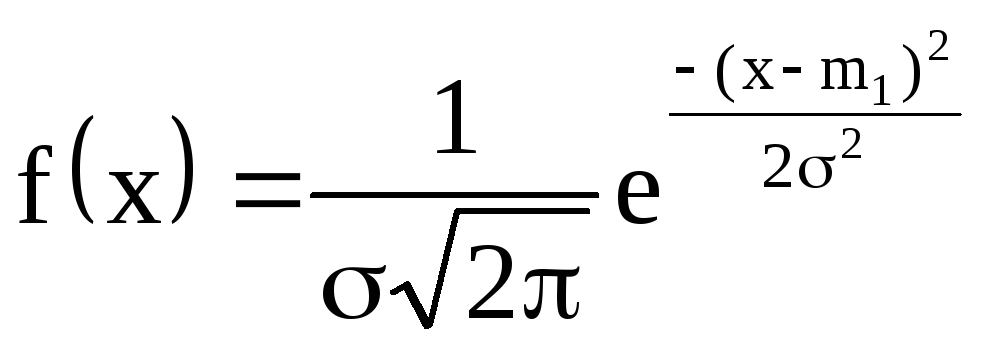лучайной величиных с математическим ожиданием и диспер-сией  имеет вид:

Реально даже воздействие ограниченного числа возмущений приводит к нормальному распределению результатов измерений и их погрешностей. В настоящее время наиболее полно разработан математический аппарат именно для случайных величин, имеющих нормальное распределение. Если же предположение о нормальности распределения отвергается, то статистическая обработка наблюдений существенно усложняется и в таком случае невозможно рекомендовать общую методику статистической обработки наблюдений. Часто даже не известно, какая характеристика распределения может служить оценкой истинного значения измеряемой величины.

Выше приведено аналитическое выражение нормального распределения для случайной измеряемой величины х. Переход к нормальному распределению случайных погрешностей осуществляется переносом центра распределений ви откладывания по оси абсцисс погрешности .

Нормальное распределение характеризуется двумя парамет-рами: математическим ожиданием m₁ и средним квадратическим отклонением σ.

При многократных измерениях несмещенной, состоятельной и эффективной оценкой m₁ для группы из n наблюдений является среднее арифметическое :

.

Нужно сказать, что среднее арифметическое дает оценку математического ожидания результата наблюдений и может быть оценкой истинного (действительного) значения измеряемой величины только после исключения систематических погрешностей.

Оценка S среднего квадратического отклонения (СКО) дается формулой:

Эта оценка характеризует рассеяние единичных результатов измерений в ряду равноточных измерений одной и той же величины около их среднего значения.

Другими оценками рассеяния результатов в ряду измерений являются размах (разница между наибольшим и наименьшим значением), модуль средней арифметической погрешности (арифметическая сумма погрешностей, деленная на число измерений) и доверительная граница погрешности (подробно рассматривается ниже).

СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:

.

Оценка S характеризует рассеяние единичных результатов наблюдений относительно среднего значения, то есть в случае, если мы за результат измерений примем отдельный исправленный результат наблюдений. Если же в качестве результата измерений принимается среднее арифметическое, то СКО этого среднего определяется по формуле:

Нормальное распределение погрешностей имеет следующие свойства:

1. симметричность, т.е. погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто;

2. математическое ожидание случайной погрешности равно нулю;

3. малые погрешности более вероятны, чем большие;

4. чем меньше , тем меньше рассеяние результатов наблюдений и больше вероятность малых погрешностей.

Другим распространенным в метрологии распределением случайной величины является равномерное распределение  распределение, при котором случайная величина принимает значения в пределах конечного интервала от х₁ до х₂ с постоянной плотностью вероятностей.

Дифференциальная функция равномерного распределения имеет вид:

f(x) = с при х₁  x  х₂

f(x) = 0 при х₂  x  х₁

При нормировке площади кривой распределения на единицу, получаем, что с(х₂ – х₁) = 1 и с = 1/ (х₂ – х₁).

Равномерное распределение характеризуется математичес-ким ожиданием, дисперсиейили СКО_.

Кроме рассмотренных примеров распределений случайных величин существуют и другие важные для практического использования распределения дискретных случайных величин, например, биномиальное распределение и распределение Пуассона. В настоящем курсе они не рассматриваются.