4.1.1 Статичний момент площі. Центр ваги перерізу

Статичним моментом S_z або S_y площі перерізу відносно осі z або y, які лежать у площині перерізу, називаються інтеграли виду

, (4.1)

де z та y  відстані від центра елементарної площадки до осей Oz та Oy .

У більшості практичних (інженерних) задач можна інтегрування замінити сумою, розділивши переріз на частини, площі і положення центрів ваги яких відомі, наприклад, переріз на рис. 4.2 можна розділити на окремі прямокутники. Тоді замість (4.1) можна записати

(4.2)

де n  кількість окремих частин перерізу,

А_i  площа частини перерізу,

z_i , y_i  відстані від центра ваги цієї площі до осей Oz та Oy.

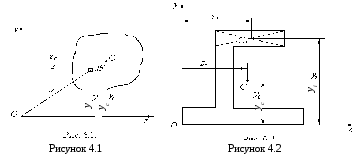
Положення центра ваги перерізу C відносно будь-яких осей z та y (рисунки 4.1 і 4.2) визначається за формулами

, (4.3)

де А площа перерізу,

S_z та S_y  статичні моменти площі перерізу відносно осей z та y.

Статичний момент площі може бути величиною додатною, від’ємною і дорівнювати нулю. Статичний момент відносно осі, яка проходить через центр ваги фігури (центральної осі) дорівнює нулю.

4.1.2 Моменти інерції перерізу

Осьовими моментами інерції I_z та I_y перерізу відносно будь-яких осей z та y, що лежать у площині перерізу (рисунок 4.1) називають інтеграли виду

, (4.4)

де y та z  відстані від елементарної площадки dА до осей Oz та Oy.

Відцентровим моментом інерції I_zy перерізу відносно осей Oz та Oy, які лежать у площині перерізу, називається інтеграл виду

. (4.5)

Інтеграл від добутків елементарних площадок на квадрати їх відстаней до даної точки (полюса) O (рисунок 4.1) називається полярним моментом інерції

. (4.6)

Осьові і полярний моменти інерції завжди додатні, відцентровий момент інерції може бути додатним, від’ємним і рівним нулю.

Якщо полюс О збігається з початком координатних осей z, y, то

I_p=I_z+I_y. (4.7)

Із (4.7) випливає, що при повороті осей координат сума осьових моментів інерції залишається незмінною.

За формулами (4.4  4.6) легко підрахувати моменти інерції для перерізів, які часто зустрічаються на практиці. Наприклад, для прямокутника (рисунок 4.3)

. (4.8)

Для круга

. (4.9)

для трикутника відносно центральної осі паралельної основі

. (4.10)

Полярний момент інерції круга відносно полюса, розміщеного в центрі ваги

. (4.11)

4.1.3 Формули переходу до паралельних або повернутих осей

Нехай система координат z_Cy_C проходить через центр ваги C перерізу (рисунок 4.4), а друга система yz, що має початок у точці O, паралельна їй. Відстані між осями цих систем позначимо через a і b. Якщо відомі моменти інерції площі А відносно центральних осей z_C і y_C  , то відносно осейz , y, паралельних центральним осям (рисунок 4.4) моменти інерції знаходять за формулами

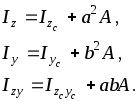(4.12)

При повороті координатних осей на кут  (рисунок 4.5) залежність між моментами інерції така:

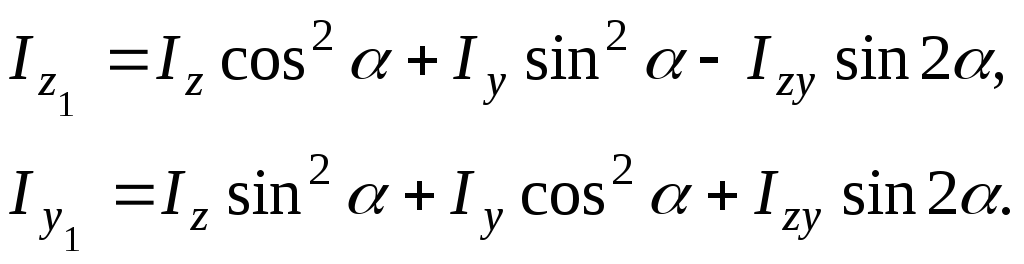(4.13)

. (4.14)

Кут  при повороті осей проти стрілки годинника.

Момент інерції складної фігури (рисунок 4.2) дорівнює сумі моментів інерції простих фігур

(4.15)

де n  кількість окремих частин перерізу,

момент інерції і-тої частини відносно довільно вибраних осей z, y. Тобто, для кожної частини вони взяті відносно одних і тих же осей.