Прямые методы решения систем линейных уравнений.

Цель работы

Цель работы – научиться решать системы линейных алгебраических уравнений, используя прямые методы решения

Задание

1. Решить систему линейных уравнений по формулам Крамера.

2. Решить систему линейных уравнений методом Гаусса.

3. Решить систему линейных уравнений методом прогонки для систем с трехдиагональной матрицей

Математическое описание

1. Метод Крамера

Требуется найти решение системы линейных уравнений

Ax = b, (1.1)

где – квадратная матрица коэффициентов при неизвестных;– вектор-столбец неизвестных; – вектор-столбец правых частей системы. По правилу Крамера системыn неизвестными имеет единственное решение, если определитель системы отличен от нуля и значение каждого из неизвестных вычисляется как отношение двух определителей порядкаn, т. е.

j =1, …, n. (1.2)

Здесь – определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом правых частей.

2. Метод Гаусса

Систему уравнений (1.1) представим в виде

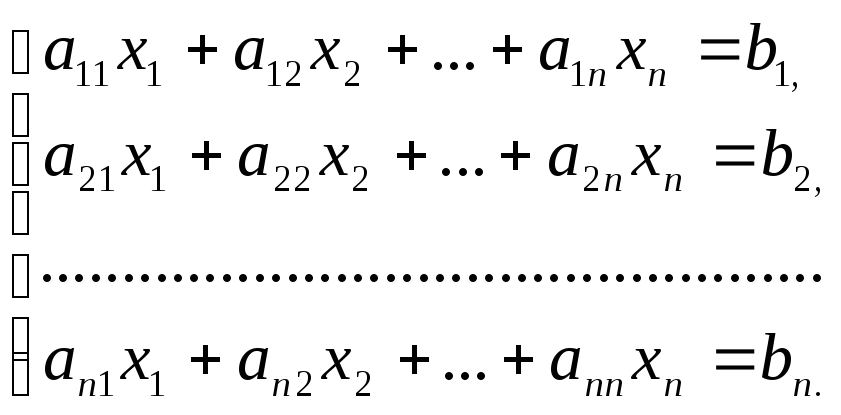(2.1)

или

i = 1,…, n.

Метод Гаусса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход), а далее – к единичной (обратный ход).

Пусть матрица система (2.1) – верхняя треугольная, поэтому приi > j, т. е. все элементы ниже главной диагонали равны нулю. Тогда из последнего уравнения сразу определяем . Подставляя в предпоследнее уравнение, находим и т. д.

Общие формулы имеют вид

при k = n (2.2)

при k = n – 1, n – 2, …, 1.

При k > l коэффициенты .

Приведем матрицу системы (1.3) к верхней треугольной. Вычтем из второго уравнения системы (1.3) первое, умноженное на такое число, при котором коэффициент при обратится в нуль. То же проделаем со всеми остальными уравнениями. В результате все коэффициенты первого столбца, лежащие ниже главной диагонали, обратятся в нуль. Затем, используя второе уравнение, обратим в нуль соответствующие коэффициенты второго столбца. Последовательно продолжая этот процесс, приведем матрицу систему к верхней треугольной форме.

Запишем общие формулы метода Гаусса. Пусть проведено исключение коэффициентов из (k-1)-го столбца. Тогда останутся уравнения с ненулевыми элементами ниже главной диагонали:

Умножим k-ю строку на число m > k и вычтем из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам

k < m.

Весь процесс приведения называется ПРЯМЫМ ХОДОМ МЕТОДА ГАУССА. Вычисление неизвестных по формулам (1.4) называют ОБРАТНЫМ ХОДОМ метода.

3. Метод прогонки для решения систем линейных уравнений с трехдиагональной матрицей

Метод прогонки принадлежит к числу прямых методов решения систем линейных уравнений и используется в тех случаях, в которых многие коэффициенты матрицы равны нулю. В методе прогонки применительно к системе линейных уравнений, имеющих трехдиагональную матрицу, можно выделить следующие этапы.

• Приведение трехдиагональной матрицы к верхней треугольной (прямой ход), В случае трехдиагональной матрицы это означает приведение к двухдиагональной, т. е. приведение исходной системы к системе, содержащей по два неизвестных в каждом уравнении, кроме последнего, в котором содержится только одно неизвестное.

• Запись обратного хода в виде , так как преобразованная матрица – двухдиагональная.

•Вывод рекуррентного соотношения для ичерезии получение соотношения дляи.

• Осуществление обратного хода метода прогонки и определение всех неизвестных.

Запишем систему линейных алгебраических уравнений с трехдиагональной матрицей в виде

i = 1,2,…, n, (3.1)

Матрица системы (1.6) имеет вид:

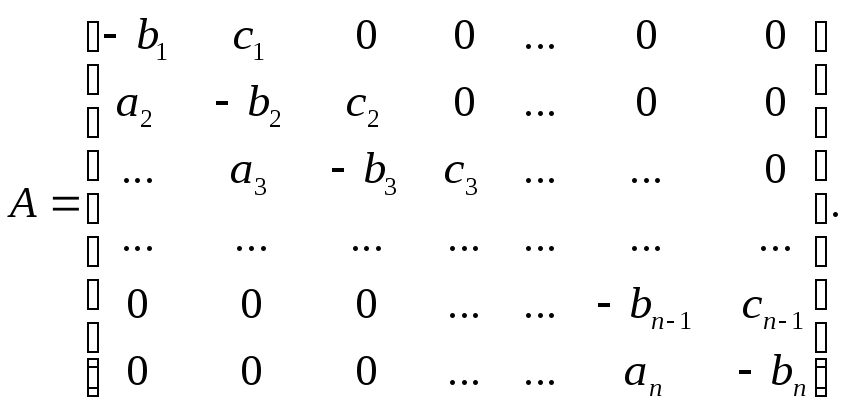
Прямой ход метода прогонки сводится к исключению неизвестного в каждом уравнении системы. Получаемая в результате прямого хода система содержит в каждом уравнении только два неизвестныхи, и матрица ее – верхняя треугольная с двумя диагоналями. Запишемi-ю строку преобразованной двухдиагональной матрицы в виде

(3.2)

Если система (3.1) приведена к виду (3.2), то обратный ход метода Гаусса очевиден. Однако использование общих алгоритмов прямого и обратного хода нецелесообразно. Построим эффективную вычислительную схему, которая и составляет суть метода прогонки. Для этого, уменьшив в (3.2) индекс на единицу, запишем

Подставляя в систему (3.1), получим соотношение

из которого нетрудно получить

Сравнивая это соотношение с (3.2), можем записать рекуррентные соотношения

(3.3)

для вычисления так называемых ПРОГОНОЧНЫХ КОЭФФИЦИЕНТОВ.

Для начала прямого хода метода прогонки необходимо задать начальные (стартовые) значения прогоночных коэффициентов, например,Начальные значения коэффициентовв рассмотренной схеме вычислений не требуются, так как значения коэффициентоввычисляются только через коэффициенты первого уравнения системы (3.1): приi = 1 из (3.1) получаем соотношение Сравнивая это выражение с (3.2) приi =1, получаем а значениев обратном ходе вычисляем по соотношениюДля начала обратного хода метода прогонки необходимо для вычислениязадать значение. Так как, то из первого соотношения (3.3) вытекает, чтои, следовательно, можно задать любое значение дляОбычно полагают ,и тогда