
- •Высшая математика
- •II курса очной формы обучения
- •Оглавление
- •Глава 1. Комплексные числа
- •1.1. Основные понятия
- •1.2. Операции над комплексными числами
- •Глава 2. Матрицы и операции над ними
- •2.1. Основные понятия
- •2.2. Операции над матрицами
- •2.3. Обратная матрица. Матричные уравнения и системы линейных уравнений
- •Решение систем линейных уравнений с помощью обратной матрицы
- •2.4. Собственные числа и собственные векторы матрицы
- •Глава 3. Дифференциальные уравнения
- •3.1. Понятия о дифференциальном уравнении
- •3.2. Уравнения с разделяющимися переменными
- •3.3. Линейные дифференциальные уравнения 1-го порядка
- •Глава 4. Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Глава 5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •Второго порядка с постоянными коэффициентами
- •5.2 Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- •Глава 6. Линейные неоднородные
- •Метод вариации произвольных постоянных (метод Лагранжа)
- •Глава 7. Элементы операционного исчисления
- •7.1. Преобразование Лапласа. Оригинал и изображение
- •7.2. Решение задачи Коши для линейных дифференциальных уравнений
- •Глава 8. Интегрирование однородных систем с постоянными коэффициентами
- •Глава 9. Ряды
- •9.1. Числовые ряды с положительными членами
- •9.2. Знакочередующиеся ряды
- •9.3. Степенные ряды
- •9.4. Разложение функций в степенные ряды
- •9.5. Ряды Фурье
- •Список рекомендуемой литературы Основная
- •Дополнительная
7.2. Решение задачи Коши для линейных дифференциальных уравнений
Методы операционного исчисления удобно применять при решении некоторых дифференциальных уравнений.
Пусть задано дифференциальное уравнение, например 2-го порядка с постоянными коэффициентами:
a0x"(t)+a1x'(t)+a2x(t)=f(t),
где а0, а1, а2=const. Требуется найти решение этого уравнения, удовлетворяющее начальным условиям: х(0)=х1, x'(0)=x2. Предположим, что правая часть данного уравнения является оригиналом. Тогда и решение x(t) этого уравнения тоже будет оригиналом. Пусть x(t) X(p), тогда
x'(t)pX(p)-x(0)=pX(p)-x1
x"(t)p2X(p)-px(0)-x'(0)=p2X(p)-px1-x2.
Далее находим изображение функции f(t) F(p).
Наконец, применяя преобразование Лапласа к обеим частям уравнения и пользуясь свойством линейности преобразования Лапласа, получаем операторное уравнение:
a0(p2X(p)-px1-x2)+a1(pX(p)-x1)+a2X(p)=F(p).
Это уравнение является линейным относительно известной функции X(p). Решая его, находим Х(р) и затем по Х(р) восстанавливаем оригинал f(t).
_______________________
Средствами операторного исчисления решить линейные (однородные и неоднородные) дифференциальные уравнения (всюду x=x(t)):
x'+3x=0, x(0)=2.
x'-4x=1-4t, x(0)=1.
x"+ 4x'-5x=0, x(0)=3, x'(0)=-3.
x"-6 x'+9x=0, x(0)=1, x'(0)=2.
x"- x'=sint, x(0)=-1, x'(0)=0.
x"+2x'+x=t+2, x(0)=0, x'(0)=2.
x"- x'=et, x(0)=x'(0)=4.
x"-3x'+10x=9sint-3cost, x(0)=0, x'(0)=-2.
x"+2 x'+x=t, x(0)=x'(0)=0.
x"+2x'+10x=sin3t+6cos3t, x(0)=x'(0)=1.
Ответы:
1. 2е-3t;
2. е4t+t;
3. 2еt+е-5t;
4. е3t-tе3t ;
5.
![]() ;
;
6. tе-t+t; 7. tеt+3еt+1; 8. е2t-е5t+sint; 9. tе-t+2е-t+t-2 ;
10. е-tcos3t-е-tsin3t+sin3t.
Глава 8. Интегрирование однородных систем с постоянными коэффициентами
Найти общее решение систем дифференциальных уравнений и, где указано, выделить частное решение, удовлетворяющее поставленным начальным условиям:
1.
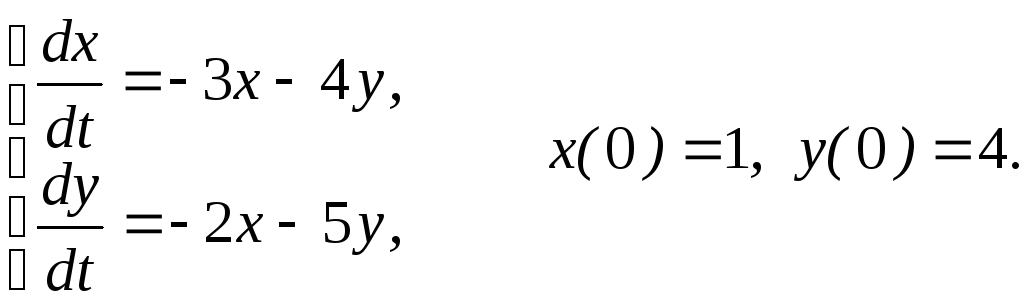
2.
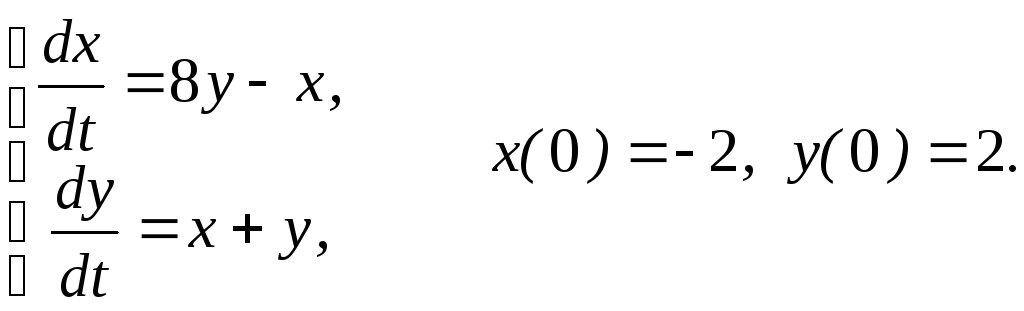
3.
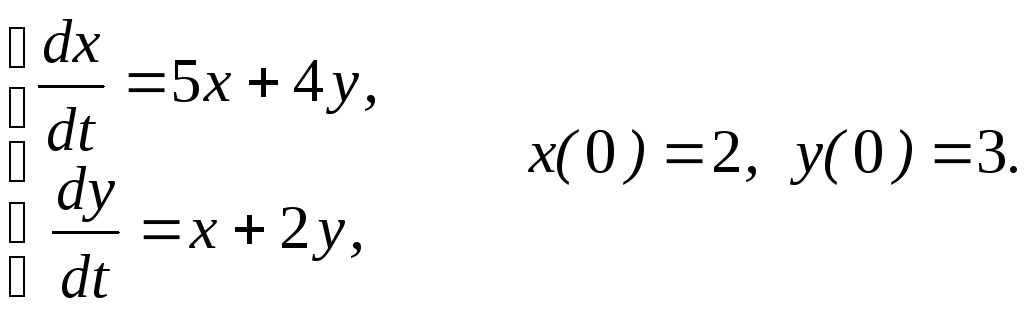
4.

5.

6.
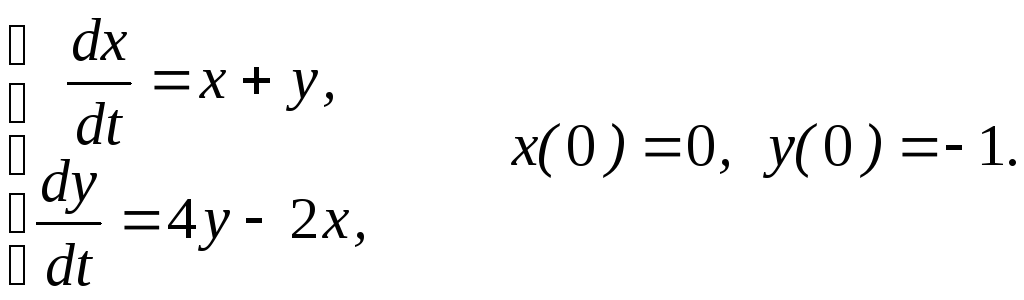
Ответы:
1.
![]() 2.
2.![]() 3.
3.![]()
4.
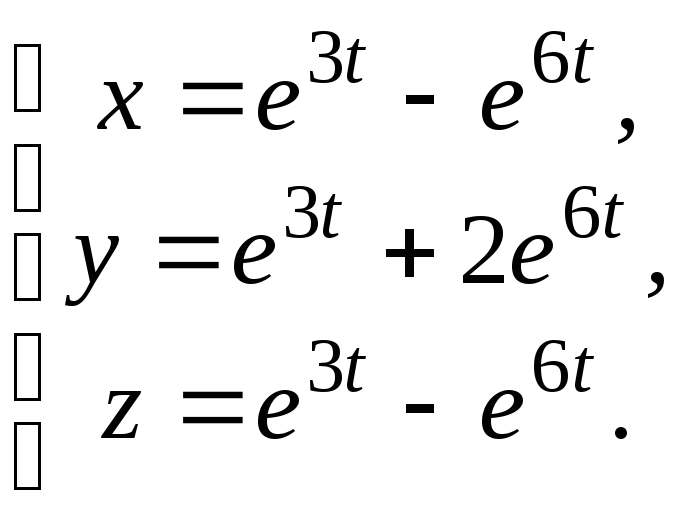 5.
5.![]() 6.
6.![]()
Глава 9. Ряды
9.1. Числовые ряды с положительными членами
Пусть задана бесконечная последовательность чисел а1, а2,…, аn,… .
Числовым рядом называется выражение вида
а1+а2+
а3+
аn+…
=![]() .
.
Числа а1, а2,…, аn,… называются членами ряда, число аn – общим членом ряда.
Суммы вида S1= а1, S2= а1 + а2, S3= а1 + а2 +а3,…, Sn= а1 + а2 +…+аn называются частичными суммами.
Числовой ряд
называется сходящимся, если существует
конечный предел последовательности
его частичных сумм
![]() ,
в противном случае ряд называется
расходящимся.
,
в противном случае ряд называется
расходящимся.
Необходимый признак сходимости
Если ряд
![]() сходится,
то общий член рядаn
стремится к нулю, т.е.
сходится,
то общий член рядаn
стремится к нулю, т.е.
![]() .
.
Если
![]() ,
то ряд расходится.
,
то ряд расходится.
Признаки сходимости рядов с положительными членами
1-й признак сравнения
Пусть
![]() и
и![]() - ряды с положительными членами, причемanbn
для всех номеров, начиная с некоторого
n=k.
Тогда
- ряды с положительными членами, причемanbn
для всех номеров, начиная с некоторого
n=k.
Тогда
если ряд
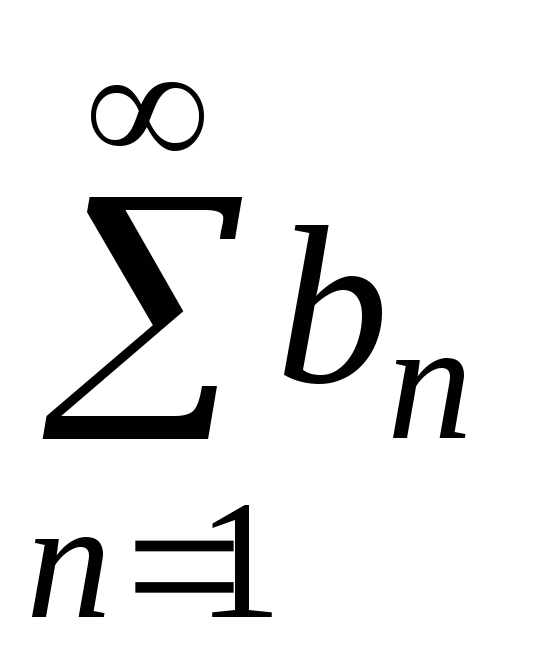 сходится,
то сходится и ряд
сходится,
то сходится и ряд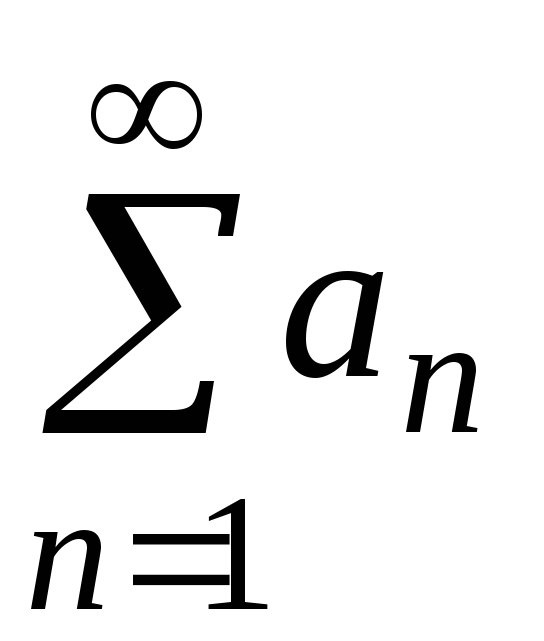 ;
;если ряд
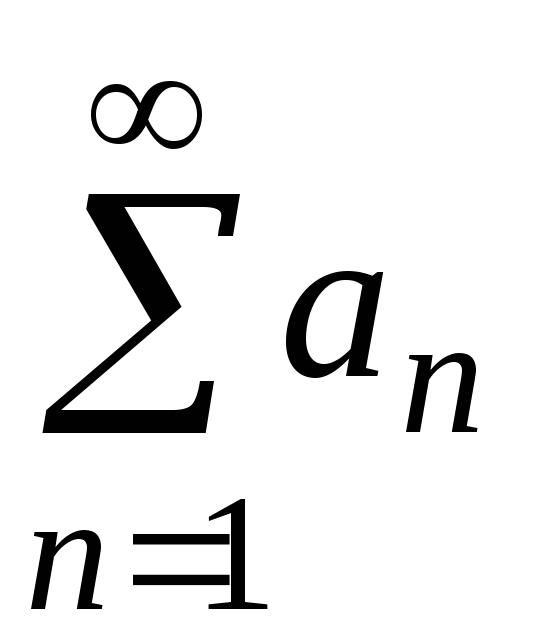 расходится, то расходится и ряд
расходится, то расходится и ряд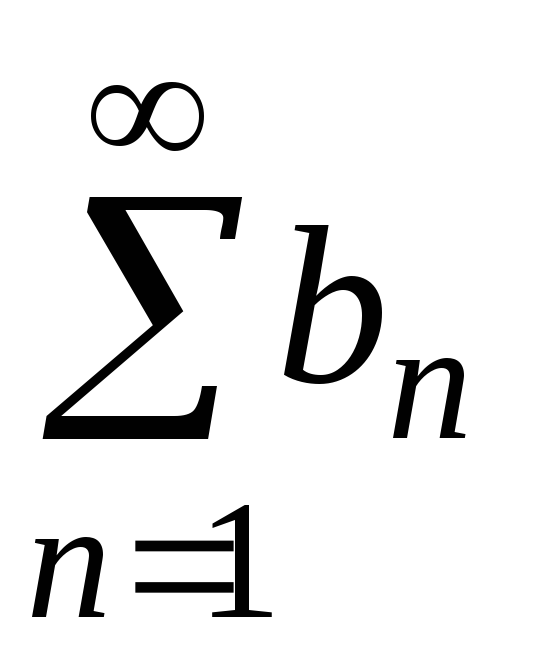 .
.
2-й признак сравнения
Пусть
![]() и
и![]() -
ряды с положительными членами и пусть
существует конечный, отличный от нуля
предел
-
ряды с положительными членами и пусть
существует конечный, отличный от нуля
предел![]() .
Тогда оба ряда ведут себя одинаково,
т.е. сходятся или расходятся одновременно.
.
Тогда оба ряда ведут себя одинаково,
т.е. сходятся или расходятся одновременно.
Для сравнения часто используются следующие ряды:
1)
![]() ,
при этом, если1,
то ряд сходится, если 1,
то ряд расходится;
,
при этом, если1,
то ряд сходится, если 1,
то ряд расходится;
2)
![]() ,
если |q|<1,
то ряд сходится; в противном случае –
расходится.
,
если |q|<1,
то ряд сходится; в противном случае –
расходится.
Признак Даламбера
Пусть
![]() - ряд с положительными членами, и
существует конечный предел.
- ряд с положительными членами, и
существует конечный предел.
![]() ,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится. Если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится. Если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
Признак Коши
Пусть
![]() - ряд с положительными членами и существует
конечный предел:
- ряд с положительными членами и существует
конечный предел:
![]() ,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится, если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
,
тогда если k<1,
то ряд сходится, если k>1,
то ряд расходится, если k=1,
то ряд может как сходиться, так и
расходиться; в этом случае требуется
исследовать ряд другими методами.
Интегральный признак сходимости
Пусть
![]() - ряд с положительными членами, для
которого существует положительная,
непрерывная и монотонно убывающая на
промежутке [1;)
функция f(x)
такая, что f(n)=an,
n=1;2;….
Тогда ряд
- ряд с положительными членами, для
которого существует положительная,
непрерывная и монотонно убывающая на
промежутке [1;)
функция f(x)
такая, что f(n)=an,
n=1;2;….
Тогда ряд
![]() и несобственный интеграл
и несобственный интеграл![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
1. Для следующих рядов проверить необходимый признак сходимости:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() .
.
2. Исследовать на сходимость ряд, применяя 1-й признак сравнения
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() .
.
3. Исследовать ряд на сходимость, применяя 2-й признак сравнения:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ;
з)
;
з)![]() .
.
4. Исследовать ряд на сходимость, используя признак Даламбера
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
5. Исследовать ряды на сходимость, применяя признак Коши:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
6. Применяя интегральный признак, исследовать ряды на сходимость:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
7. Исследовать на сходимость следующие ряды:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() ;
;
е)
![]() ;
ж)
;
ж)![]() ;
з)
;
з)![]() ;
и)
;
и)![]() .
.
_______________________
Ответы:
1. а) расходится;
б)
![]() ;
в) расходится; г) расходится;
;
в) расходится; г) расходится;
д)
![]() ;
е) расходится.
;
е) расходится.
2. а) сходится; б) расходится; в) расходится; г) сходится;
д) расходится.
3. а) расходится; б) сходится; в) расходится; г) расходится;
д) расходится; е) сходится; ж) сходится; з) сходится.
4. а) расходится; б) сходится; в) сходится; г) сходится;
д) расходится; е) сходится.
5. а) расходится; б) сходится; в) сходится.
6. а) расходится; б) расходится; в) расходится.
7. а) расходится; б) расходится; в) расходится; г) сходится;
д) сходится; е) сходится; ж) расходится; з) сходится;
и) расходится.
