
- •Внимание!!! контрольная работа должна быть выполнена в рукописном виде. Иначе она принята не будет. Варианты с 6 по 10.
- •1. Типы уравнений второго порядка в частных производных. Приведение к каноническому виду
- •Задания для самостоятельной работы
- •Составим уравнение движения струны. На элемент струны (х,) действуют силы натяженияи внешняя сила, действующая на струну в точкехв момент времениtи направленная перпендикулярно осиОх.
- •2.2. Формула Даламбера
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •2.5. Решение краевой задачи методом Фурье
- •Задания для самостоятельной работы
- •3.2. Решение краевых задач методом Фурье
- •3.3. Неоднородное уравнение теплопроводности Рассмотрим задачу для неоднородного уравнения теплопроводности
- •Задания для самостоятельной работы
- •3.5. Решение уравнения теплопроводности методом Тейлора
- •Задания для самостоятельной работы
- •Или. (158)
- •Задания для самостоятельной работы
Задания для самостоятельной работы
Определить тип уравнения и привести к каноническому виду
1.
![]() .
2.
.
2.![]() .
3.
.
3.![]() .
.
4.
![]() .
5.
.
5.![]() .
.
6.
![]() .
.
7.
![]() .
.
2. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
2.1. Уравнение колебаний струны
Рассмотрим
струну, под которой понимается тонкая
нить, не сопротивляющаяся изгибу, длиной
l
. Пусть эта струна в плоскости (x,u)
совершает малые поперечные колебания
около своего положения равновесия,
совпадающего с осью Ох,
то есть все точки струны движутся
перпендикулярно оси Ох.
Обозначим через u(x,t)
отклонение от положения равновесия
точки струны с абсциссой
х в момент
времени t.
Так как струна не сопротивляется изгибу,
то ее натяжение
![]() в точкех
в момент времени t
направлено по касательной к струне в
точке х.
Любой участок струны (а,b)
после
отклонения от положения равновесия в
предположении о пренебрежении величинами
высшего порядка малости по сравнению
с
в точкех
в момент времени t
направлено по касательной к струне в
точке х.
Любой участок струны (а,b)
после
отклонения от положения равновесия в
предположении о пренебрежении величинами
высшего порядка малости по сравнению
с
![]() ,
не изменит своей длины
,
не изменит своей длины
![]() (16)
(16)
и,
следовательно, величина натяжения
![]() будет постояннойТ0,
не зависящей от х
и t,
так как закон Гука гласит: изменение
натяжения пропорционально изменению
длины выделенного участка.
будет постояннойТ0,
не зависящей от х
и t,
так как закон Гука гласит: изменение
натяжения пропорционально изменению
длины выделенного участка.
Составим уравнение движения струны. На элемент струны (х,) действуют силы натяженияи внешняя сила, действующая на струну в точкехв момент времениtи направленная перпендикулярно осиОх.
Сумма сил, действующих на струну, согласно закону Ньютона должна быть равна произведению массы элемента струны на его ускорение
![]() , (17)
, (17)
где
![]() -
масса элемента струны (х,
-
масса элемента струны (х,
![]() );
);
![]() -
единичный вектор, направленный вдоль
оси u.
-
единичный вектор, направленный вдоль
оси u.
Проектируя векторное равенство (17) на ось u, получим
![]() , (18)
, (18)
но в рамках приближения
![]() ,
,
поэтому выражение (18) принимает вид
![]()
и
при
![]() ,
получим
,
получим
![]() . (19)
. (19)
Это и есть уравнение малых поперечных колебаний струны. Если F(x,t)0, то колебания струны будут вынужденными, а если F(x,t)=0, то колебания струны будут свободными.
Если
![]() ,
то уравнение (19) принимает вид
,
то уравнение (19) принимает вид
![]() , (20)
, (20)
где
![]() .
.
Уравнение (20) называется одномерным волновым уравнением. Для волнового уравнения может быть поставлена задача Коши, и в этом случае необходимо найти функцию u(x,t), удовлетворяющую начальным условиям
![]()
где
![]() -
заданные функции.
-
заданные функции.
2.2. Формула Даламбера
Поставим задачу Коши для однородного волнового уравнения, т.е. найдем решение уравнения
![]() , (21)
, (21)
удовлетворяющее начальным условиям
![]() . (22)
. (22)
Эту задачу (21), (22) можно решить методом Даламбера. Введем новые переменные
![]() .
.
Вычислим
![]() :
:
![]()
и подставим их в уравнение (21)
![]() .
.
После сокращений получим
![]() . (23)
. (23)
Интегрирование этого уравнения дает

Возвращаясь к переменным х и у, окончательно будем иметь
![]() . (24)
. (24)
Функция
![]() является решением уравнения (21), еслии1
и и2
- произвольные дважды дифференцируемые
функции. В решении (24) необходимо выбрать
функции и1
и и2
так, чтобы удовлетворить начальным
условиям (22)
является решением уравнения (21), еслии1
и и2
- произвольные дважды дифференцируемые
функции. В решении (24) необходимо выбрать
функции и1
и и2
так, чтобы удовлетворить начальным
условиям (22)
![]() (25)
(25)
и
![]() .
(26)
.
(26)
Проинтегрировав уравнение (26) в пределах от х0 до х, получим
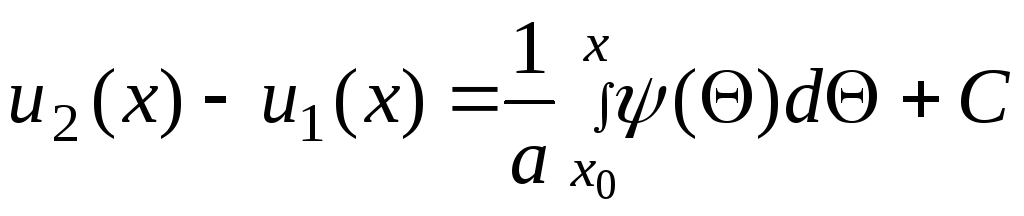 .
(27)
.
(27)
Разрешив совместно уравнения (25) и (27) относительно и1(х) и и2(х), получим
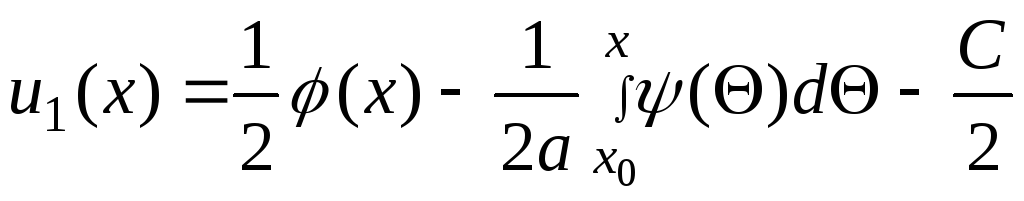 (28)
(28)
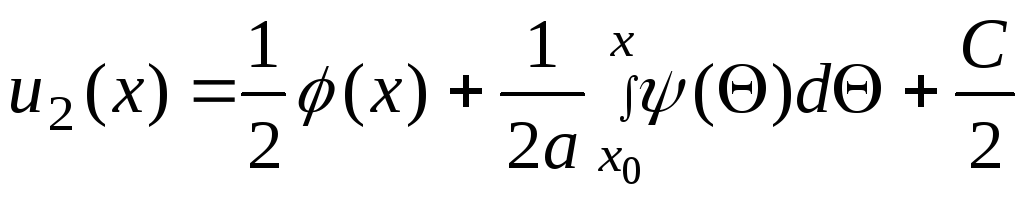 (29)
(29)
Подставив (28) и (29) в решение (24) окончательно получим решение задачи Коши для однородного волнового уравнения
![]() .
(30)
.
(30)
Формула
(30) называется формулой
Даламбера
для однородного волнового уравнения.
Эта формула дает классическое решение
задачи (21), (22) только в предположении,
что функция
![]() имеет производные до второго порядка
включительно, а функция
имеет производные до второго порядка
включительно, а функция![]() - до первого.
- до первого.
Пример 6. Найти решение уравнения
![]() ,
,
удовлетворяющее начальным условиям
![]() .
.
▲ Для нахождения решения исходной задачи Коши используем формулу Даламбера (30)
![]() ,
,
в
которой
![]() .
.
Следовательно,
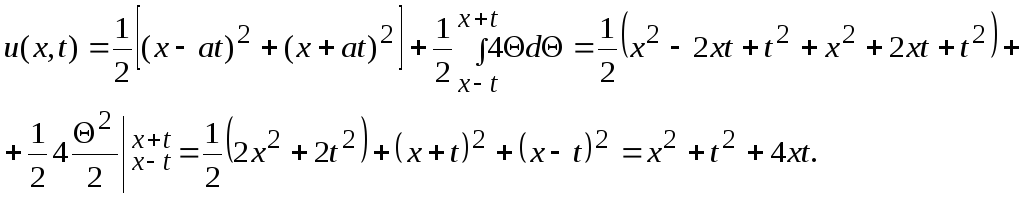 Окончательно
решение исходной задачи имеет вид
Окончательно
решение исходной задачи имеет вид
![]() ▲
▲
Рассмотрим задачу Коши для неоднородного волнового уравнения
![]() , (31)
, (31)
![]() . (32)
. (32)
Пусть
![]() есть решение вспомогательной задачи
Коши
есть решение вспомогательной задачи
Коши
![]() , (33)
, (33)
При
![]()
![]() . (34)
. (34)
Формула Даламбера (30) дает
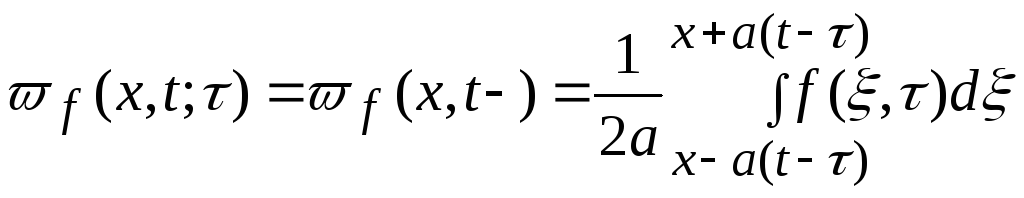 .
(35)
.
(35)
Перепишем формулу Даламбера (30) в виде
![]() , (36)
, (36)
где
![]()
являются
решениями задачи (33), (34) при
![]() и
и![]() соответственно, т.к. непосредственное
дифференцирование показывает, что
соответственно, т.к. непосредственное
дифференцирование показывает, что
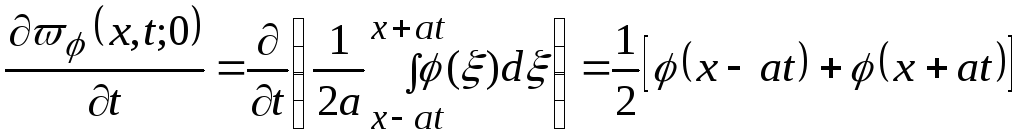 .
.
Решение неоднородного уравнения (31) с нулевыми начальными условиями
![]()
имеет вид
![]() . (37)
. (37)
Поэтому в силу (36) и (37) решение исходной задачи (31), (32) можно представить в виде
![]() . (38)
. (38)
Таким образом, с учетом (35), окончательно получим
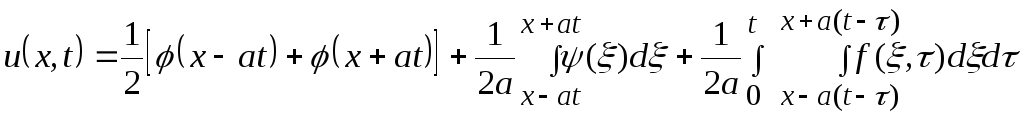 .(39)
.(39)
Это формула Даламбера, которая дает решения задачи Коши для неоднородного волнового уравнения.
Пример 7. Найти решение уравнения
![]() ,
,
удовлетворяющее начальным условиям
![]() .
.
▲ Для нахождения решения исходной задачи Коши используем формулу Даламбера (39)
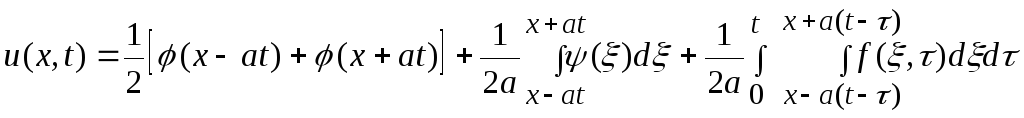 в
которой
в
которой
![]() .
.
Следовательно,
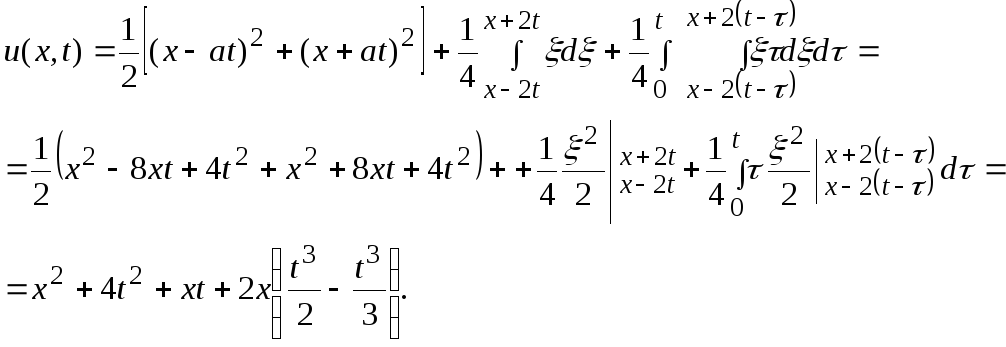 Окончательно
решение исходной задачи имеет вид
Окончательно
решение исходной задачи имеет вид
![]() ▲
▲
