
-
-
Сглаживающий функционал и его свойства
Пусть функции, входящие в уравнение
 (2.1)
(2.1)
являются непрерывными, причем
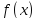 определена на интервале
определена на интервале
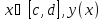 – при
– при
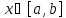 ,
а ядро K(x,s)
– в прямоугольнике
,
а ядро K(x,s)
– в прямоугольнике
 .
Запишем уравнение (2.1) в виде
.
Запишем уравнение (2.1) в виде
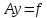 , (2.2)
, (2.2)
где А – оператор Фредгольма. Рассмотрим функционал
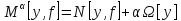 ,
(2.3)
,
(2.3)
где
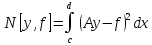 , (2.4)
, (2.4)
 ,
,
 ,
,
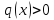 . (2.5)
. (2.5)
Здесь α>0 – некоторый параметр,
называемый параметром регуляризации.
Функционал (3.5) называется регуляризирующим,
а функционал
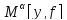 – сглаживающим функционалом.
– сглаживающим функционалом.
Поставим вариационную задачу на экстремум
функционала
 .
Экстремум будем искать в классе Y
функций y(x),
дважды непрерывно дифференцируемых и
удовлетворяющих условия
.
Экстремум будем искать в классе Y
функций y(x),
дважды непрерывно дифференцируемых и
удовлетворяющих условия
 (2.6)
(2.6)
Пусть
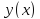 и
и
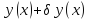 - две функции, принадлежащие Y.
Вычислим приращение функционала
- две функции, принадлежащие Y.
Вычислим приращение функционала
 ,
отвечающее приращению δy,
т.е. вычислим величину
,
отвечающее приращению δy,
т.е. вычислим величину
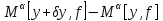 .
Имеем
.
Имеем
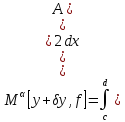
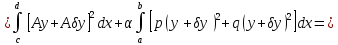
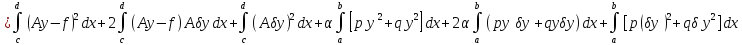 .
.
В этом выражении сумма первого и
четвертого слагаемых представляет
собой
 .
Перенесем их влево и тогда получим, что
приращение функционала
.
Перенесем их влево и тогда получим, что
приращение функционала
 распадается на линейную относительно
δy часть (эта сумма второго
и пятого слагаемых), третьего и шестого
слагаемых, зависящую от δy
нелинейно, которую обозначим
распадается на линейную относительно
δy часть (эта сумма второго
и пятого слагаемых), третьего и шестого
слагаемых, зависящую от δy
нелинейно, которую обозначим
 и которая, как нетрудно видеть, при любом
и которая, как нетрудно видеть, при любом
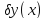 неотрицаельна:
неотрицаельна:
 . (2.7)
. (2.7)
Из вариационного исчисления известно,
что если
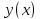 реализует экстремум функционала
реализует экстремум функционала
 ,
то δ
,
то δ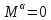 ,
т.е.
,
т.е.
 (2.8)
(2.8)
Это равенство представляет собой необходимое условие экстремума. Преобразуем первое слагаемое, изменив порядок интегрирования:
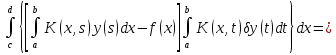
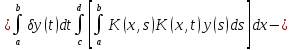

 ,
,
где
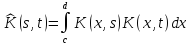 ,
,
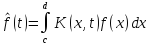 .
.
Во втором слагаемом в (3.8) произведем интегрирование по частям. Получим
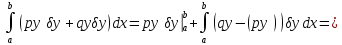
 ,
,
так как внеинтегральный член в силу (3.6) обращается в нуль. Соотношение (2.8) принимает тогда вид
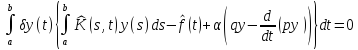 . (2.9)
. (2.9)
Поскольку δy(t)
– произвольная вариация, то, в силу
основной леммы вариационного исчисления,
выражение в фигурных скобках равно
нулю. Получаем уравнение, определяющее
экстремали функционала
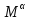 :
:
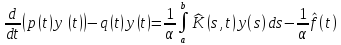 . (2.10)
. (2.10)
Таким образом, если
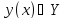 осуществляет экстремум функционала
осуществляет экстремум функционала
 при условиях (2.6), то y
удовлетворяет уравнению (2.10).
при условиях (2.6), то y
удовлетворяет уравнению (2.10).
Теорема о минимальном значении
сглаживающего функционала: Для любой
непрерывной функции
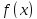 существует единственная функция
существует единственная функция
 из класса Y, на которой
реализуется минимальное значение
функционала
из класса Y, на которой
реализуется минимальное значение
функционала
 .
.
Доказательство: Докажем, что уравнение (2.10) при краевых условиях (2.6) имеет единственное решение. Уравнение (2.10) является интегро-дифференциальным уравнением. Сведем его к интегральному уравнении. Фредгольма второго рода.
Рассмотрим уравнение
 (2.11)
(2.11)
При условиях (3.6). Убедимся, что эта задача
имеет только тривиальное решение.
Действительно, пусть y(t)
имеет положительное максимальное
значение, достигающееся в некоторой
точке
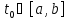 .
Тогда
.
Тогда
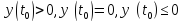 .
Учитывая, что
.
Учитывая, что
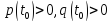 ,
имеем
,
имеем
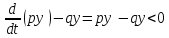 при
при
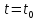 ,
что противоречит равенству (2.11).
Следовательно,
,
что противоречит равенству (2.11).
Следовательно,
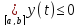 .
Аналогично доказывается, что
.
Аналогично доказывается, что
 .
Отсюда следует, что
.
Отсюда следует, что
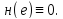
В силу доказанного, существует функция
Грина
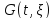 и уравнение (2.10) при условиях (2.6)
эквивалентно интегральному уравнению
и уравнение (2.10) при условиях (2.6)
эквивалентно интегральному уравнению
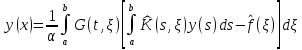 ,
,
или
 , (2.12)
, (2.12)
где
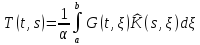 - некоторое ядро,
- некоторое ядро,
а
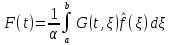 .
.
Уравнение (3.12) представляет собой интегральное уравнение Фредгольма второго рода. Докажем, что оно имеет единственное решение. Для этого, достаточно доказать, что соответствующее однородное уравнение имеет только тривиальное решение. А это эквивалентно тому, что однородное уравнение (2.10) при условиях (2.6) имеет только тривиальное решение. Допустим противное, т.е. что уравнение
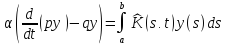 (2.13)
(2.13)
имеет нетривиальное решение y(t). Умножая (3.13) на y(t) и интегрируя, получим
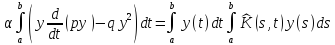 (2.14)
(2.14)
Интегрированием по частям преобразуем
левую часть к виду -
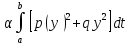 .
Правую часть преобразуем, пользуясь
выражением (2.9) для
.
Правую часть преобразуем, пользуясь
выражением (2.9) для
 и изменяя порядок интегрирования:
и изменяя порядок интегрирования:

 .
.
После этих преобразований (2.14) принимает вид
 .
.
Так как
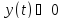 ,
то левая часть отрицательна, а правая
неотрицательна, и мы имеет противоречие,
доказывающее, что задача (2.13), (2.6) имеет
только тривиальное решение, а следовательно,
уравнение (2.12) имеет единственное
решение.
,
то левая часть отрицательна, а правая
неотрицательна, и мы имеет противоречие,
доказывающее, что задача (2.13), (2.6) имеет
только тривиальное решение, а следовательно,
уравнение (2.12) имеет единственное
решение.
Нетрудно увидеть, что это решение
реализует минимально значение функционала
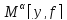 .
Это непосредственно следует из (2.7),
поскольку
.
Это непосредственно следует из (2.7),
поскольку
 при
при
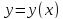 ,
а
,
а
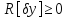 при любом
при любом
 .
Теорема доказана.
.
Теорема доказана.
