Метрология Задача 3

Тема: Статистическая обработка результатов многократных измерений

1 Теоретическая часть

Статистическая обработка результатов многократных измерений основывается на использовании большого объёма практически полученной апостериорной информации.

Цель статистической обработки результатов измерений: получить более достоверную информацию о том, в каких границах можно ожидать появление измеряемой случайной физической величины (например: измеряемого размера).

При этом решаются три задачи:

оценивание области неопределённости исходных экспериментальных данных;

нахождение более точного усреднённого результата измерений;

оценивание погрешности этого усреднённого результата, то есть нахождение более узкой области неопределённости числового появления размера.

1.1 Определения

Статистическая обработка результатов измерений – заключается в определении границ доверительного интервала в размерном ряду, в которых может появиться ожидаемый размер объекта измерения.

Апостериорная информация – та, которая получена путём проведения практических измерений.

Доверительный интервал – границы числового ряда значений случайной величины, внутри которых с определённой вероятностью будет находиться математическое ожидание этой случайной величины. Для закона нормального распределения случайных величин эти границы расположены симметрично их среднему арифметическому значению (например, измеряемый диаметр деталей круглой формы: его размер – это случайная величина).

Доверительная вероятность – вероятность, соответствующая этому доверительному интервалу.

Число степеней свободы – для закона нормального распределения случайных величин это – число интервалов в диапазоне рассеивания размеров минус 3 (три вычисляемых с помощью этих расчётов величины).

Диапазон рассеивания размеров – разность между максимальным и минимальным размерами.

Интервалы в диапазоне рассеивания размеров – отрезки оси размеров, делящие диапазон рассеивания на равные части.

Случайная величина – которая в результате опыта может принять то или иное значение, не известное заранее (например, измеряемый диаметр одинаковых деталей круглой формы).

Дискретная величина – случайная величина, которая может принять только раздельное, отделенное от соседних величин из размерного ряда значение величины (например, возможное число очков при бросании во время игры в кости).

Действительная величина – числовой результат измерения.

Выборка – некоторое небольшое количество измерений, проделанное для того чтобы по их результатам судить о более полном диапазоне рассеивания измеренной величины.

Гистограмма – график, в прямоугольных осях «частость – диапазон рассеивания измеренных значений», состоящий из вертикальных прямоугольников различной высоты и эмпирической ломаной кривой, соединяющей серединки верхних перекладин прямоугольников, отображающей закон распределения измеряемых случайных величин.

1.2 Порядок проведения статистических измерений

В некотором количестве одинаковых измерений одной и той же физической величины размерные значения несколько отличаются друг от друга .

Если количество измерений в выборке невелико, то для определения доверительного интервала более полного разброса их значений необходимо провести статистическую обработку результатов измерений.

Статистическая обработка результатов измерений производится следующим образом.

1) Располагают полученные в процессе N измерений действительные значения x_i в порядке возрастания их величины и тем самым получают ранжированный ряд случайных дискретных величин: x₁; x₂ …x_N.

2) Диапазон рассеивания R определяется как разность между максимальной x_{i max} и минимальной x_{i min} величинами действительных значений измерений:

R = x_{i max} – x_{i min} .

3) Полученное значение диапазона рассеивания разбивают на k интервалов (рекомендуется 7 – 12 интервалов. При малых выборках число интервалов равно числу групп одинаковых значений измерений). Задавшись числом интервалов, рассчитывают дискретный шаг интервалов по формуле:

p = R/k .

4) Для каждого интервала подсчитывают число измерений n_j, имеющих величину, находящуюся в пределах границ этого интервала, среднее арифметическое значение в группе измерений j-того интервала, а также частость числа измерений n_j /(N – 1) в данном интервале.

Результаты измерений и расчётов заносят в таблицу 1.

Таблица 1 – Пример записи значений случайной величины при N=9 и k=5

Номер измерения	1	2	3	4	5	6	7		8		9
xi(итое)	23	24	24	25	25	25	26		27		27
(житое)	23	24		25				26		27
nj(житое)	1	2		3				1		2
nj /(N – 1)	1/8	2/8		3/8				1/8		2/8

где x_i –значение i-того измерения;

–среднее арифметическое значение в группе измерений j-того интервала:

.

5) По экспериментальным данным строят гистограмму и эмпирическую кривую (полигон) распределения значений случайной величины. Масштаб гистограммы выбирают таким, чтобы её высота относилась к основанию примерно как 5:8.

6) Определяют среднее арифметическое значение всех замеренных действительных значений величин:

.

7) Рассеяние значений случайных величин в выборке из N измерений относительно эмпирического (опытного, практического) группирования их по интервалам характеризуется уточнённым эмпирическим средним квадратическим отклонением, которое определяется по формуле:

= ,

8) По результатам выборки устанавливают границы, внутри которых с определённой вероятностью будет находиться математическое ожидание F(x) случайной величины x. Эти границы определяют доверительный интервал, который зависит от доверительной вероятности β. В общем случае при малой выборке и различной доверительной вероятности доверительный интервал в своих меньшей и большей границах выразится следующими неравенствами:

F(x),

где 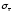- среднее квадратическое отклонение для распределения средних арифметических величин:

;

t_δ – критерий Стьюдента, который для β=0,9 (90% доверительная вероятность) при данном числе степеней свободы К (приведён в таблице 2).

Таблица 2 – Критерий Стьюдента при доверительной вероятности β=0,9 и данном числе степеней свободы К

К	15 – 16	17	18 – 20	21 – 22	23 – 27	28 – 30
tδ	1,75	1,74	1,73	1,72	1,71	1,70

9) Сравнивают границы доверительного интервала с допуском на размер (если он задан в условии задачи) и делают вывод о годности всей партии деталей.

10) Ответом на решение задачи является доверительный интервал с указанием величин его меньшей и большей границ.