
Билинейные и квадратичные функции на евклидовых пространствах
.doc§ 13. Билинейные и квадратичные функции на евклидовых пространствах.
1º. Преобразование, присоединенное к билинейной функции.
Пусть
![]() – евклидово пространство, b(x,y)
– билинейная функция на.
– евклидово пространство, b(x,y)
– билинейная функция на.
Def
1. Линейное
преобразование Â
на
![]() называется присоединенным к билинейной
функции b(x,y),
если
называется присоединенным к билинейной
функции b(x,y),
если
![]() выполнено
выполнено
b(x,y)=(x ,Ây). (1)
Утверждение 1. Каждая билинейная функция имеет присоединенное преобразование, и такое преобразование единственно.
Доказательство.
Пусть
![]() - базис в и А
– матрица Â
в этом базисе. Тогда
- базис в и А
– матрица Â
в этом базисе. Тогда
(x,Ây)=ХГAY,
где
Г – матрица Грама в базисе
![]() ,
Х,Y
– координатные столбцы x
и
y,
следовательно, (x,Ây)
– билинейная функция с матрицей ГА.
В силу единственности матрицы билинейной
функции в базисе имеем, что если у
билинейной функции b(x,y)
существует присоединенное преобразование,
то матрица В
билинейной функции равна
,
Х,Y
– координатные столбцы x
и
y,
следовательно, (x,Ây)
– билинейная функция с матрицей ГА.
В силу единственности матрицы билинейной
функции в базисе имеем, что если у
билинейной функции b(x,y)
существует присоединенное преобразование,
то матрица В
билинейной функции равна
В=ГА.
Отсюда следует
А=![]() .
.
Это означает, что
билинейная функция не может иметь больше
одного присоединенного преобразования:
если оно существует, то его матрице
равна
![]() .
.
Докажем существование
присоединенного преобразования. Для
этого надо проверить, что преобразование
с матрицей (2) является присоединенным.
Действительно, если (x,Ây)=
ХГAY![]() ХГ
ХГ![]() Y=
b(x,y).
■
Y=
b(x,y).
■
Формула (3) – это формула связи между матрицами билинейной функции и линейного преобразования, следовательно, если базис ортонормированный, то
А=В.
Если
А –
симметричная, то Â – самосопряженный
оператор
![]()
Следствие.
Присоединенное преобразование является
самосопряженным
![]() билинейная
функция является симметричной.
билинейная
функция является симметричной.
Преобразование, присоединенное к симметричной билинейной функции, называется присоединенным к соответствующей квадратичной форме.
2º. Ортонормированный базис, в котором квадратичная форма имеет диагональный вид.
Теорема1.
В евклидовом пространстве
![]() для каждой квадратичной формы существует
ортонормированный базис, в котором она
имеет диагональный вид.
для каждой квадратичной формы существует
ортонормированный базис, в котором она
имеет диагональный вид.
Доказательство. Базисом, существование которого утверждается, является ортонормированный базис из собственных векторов самосопряженного преобразования, присоединенного к квадратичной форме. В нем В=А и А – диагональная матрица. ■
Следующая теорема является по существу другой формулировкой теоремы 1.
Теорема 2. Пусть в линейном пространстве L заданы две квадратичные формы k и h, причем h положительно определенная. Тогда в L существует базис, в котором обе формы имеют диагональный вид.
Для доказательства введем в L скалярное произведение, приняв h за основную квадратичную форму. По отношению к этому скалярному произведению ортонормированными будут те базисы, в которых h имеет канонический вид. По теореме 1 для формы k существует ортонормированный базис, в котором она имеет диагональный вид. Это и есть базис, существование которого мы доказываем.
Замечание. Если пространство L евклидово, то теорема 2 останется, конечно, справедливой. Уже существующее скалярное произведение оставляется без внимания, а для доказательства вводится новое скалярное произведение при помощи формы h. Найденный базис, вообще говоря, не будет ортонормированным по отношению к старому скалярному произведению.
Теперь
приведем две квадратичные формы к
диагональному виду в одном и том же
базисе. Пусть K
и H
– матрицы квадратичных форм в исходном
базисе е.
Матрица H
является матрицей Грама базиса е
для вспомогательного скалярного
произведения. Поэтому преобразование,
присоединенное к форме k
в базисе е,
имеет матрицу
![]() .
Напишем его характеристический многочлен
.
Напишем его характеристический многочлен
![]() в виде
в виде
![]() .
Так как
.
Так как
![]() ,
характеристическое уравнение имеет те
же корни, что и уравнение
,
характеристическое уравнение имеет те
же корни, что и уравнение
![]() ,
(5)
,
(5)
называемое
обобщенным
характеристическим уравнением.
Для каждого из его корней система
уравнений собственного подпространства
![]() эквивалентна системе
эквивалентна системе
![]() .
.
Для
каждого корня фундаментальную систему
решений такой системы уравнений надо
ортогонализовать и нормировать, находя
скалярное произведение по формуле
![]() с матрицей Грама H.
Объединяя все так полученные
ортонормированные базисы собственных
подпространств, мы получаем базис
с матрицей Грама H.
Объединяя все так полученные
ортонормированные базисы собственных
подпространств, мы получаем базис
![]() .
Он ортонормирован относительно
вспомогательного скалярного произведения,
и потому форма h
в нем имеет канонический вид. Так как
он состоит из собственных векторов
преобразования, присоединенного к k,
эта форма будет иметь диагональный вид
в базисе
.
Он ортонормирован относительно
вспомогательного скалярного произведения,
и потому форма h
в нем имеет канонический вид. Так как
он состоит из собственных векторов
преобразования, присоединенного к k,
эта форма будет иметь диагональный вид
в базисе
![]() .
.
Пример. Найти матрицу перехода к базису, в котором квадратичные формы
![]() ,
,
![]()
обе имеют диагональный вид, а также их вид в этом базисе.
Решение.
Здесь
![]() - т.е. положительно определенная. Таким
образом, билинейную форму, соответствующую
- т.е. положительно определенная. Таким
образом, билинейную форму, соответствующую
![]() ,
можно взять за скалярное произведение.
,
можно взять за скалярное произведение.
Матрица
этой билинейной формы имеет вид:
![]() ,
т.е. она является матрицей Грама в
соответствующем евклидовом пространстве.
Тогда матрица присоединенного
преобразования к билинейной форме
,
т.е. она является матрицей Грама в
соответствующем евклидовом пространстве.
Тогда матрица присоединенного
преобразования к билинейной форме
![]() ,
соответствующая
,
соответствующая
![]() ,
имеет вид
,
имеет вид
![]() .
.
Найдем собственные значения А:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ~
~![]() ~
~![]()
![]() .
.
Нормировка
по скалярному произведению с
![]() :
:
![]() .
.
![]() .
.
![]() .
.
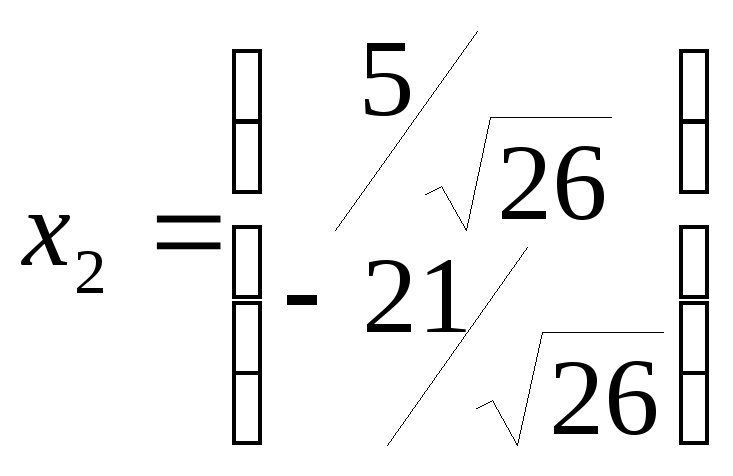 .
.
Таким
образом,
![]() и
и
![]() выбираем за новый базис, т.е.
выбираем за новый базис, т.е.
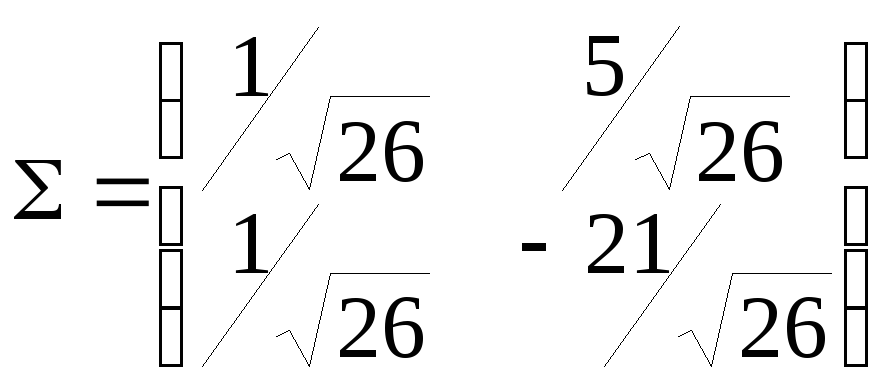 .
.
Тогда
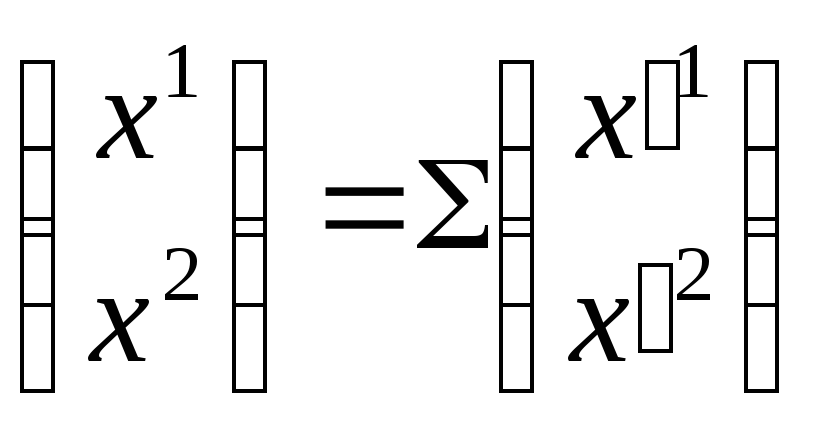
![]()
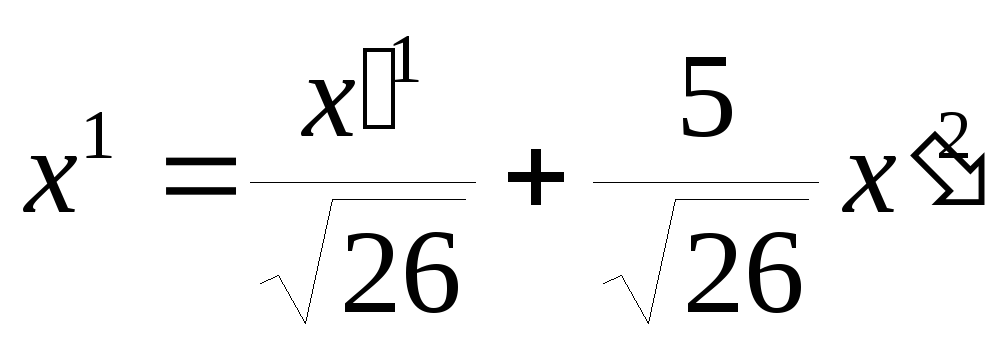 ,
,
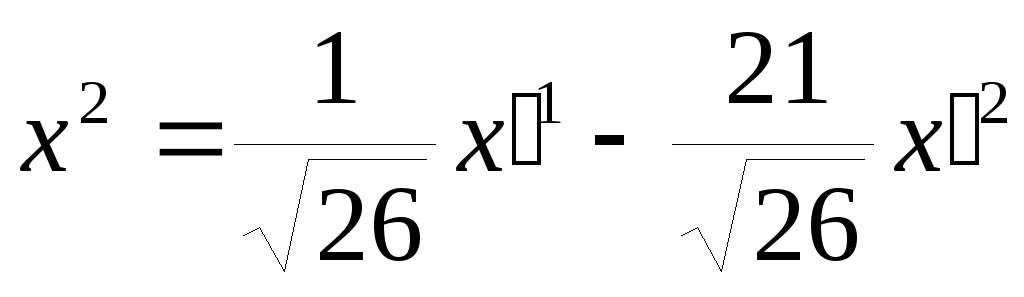 .
.

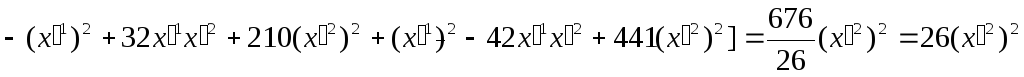
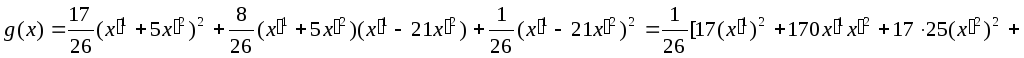
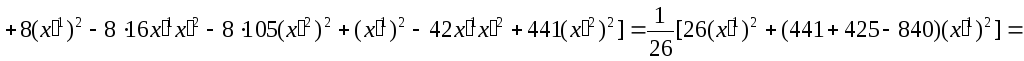
 .
.
