
- •3.Поняття частинних похідних функції n змінних. Теорема про незалежність змішаних похідних від порядку диференціювання.
- •4.Диференційованість функції n змінних. Теорема про похідну складної функції.
- •5.Повний диференціал функції n змінних. Теорема про інваріантність форми першого диференціала. Застосування диференціалу до наближених обчислень.
- •7.Локальні екстремуми функції 2-х змінних. Необхідна і достати а умови існування цих екстремумів (наслідок з формули Тейлора).
- •Частинні похідні. Повний диференціал
- •Формула Стокса (зв'язок між криволінійним інтегралом другого роду і поверхневим інтегралом).
- •Векторне поле: означення. Потік векторного поля через поверхню. Дївергенція векторного поля. Теорема Остроградського- Гауса в векторній формі.
- •Ротор векторного поля. Теорема Стокса в векторній формі.
- •Потенціальне поле. Потенціал векторного поля, його знаходження.
Частинні похідні. Повний диференціал
Означення. Нехай задано функцію z=f(x,y) і нехай деяку точку з області визначення цієї функції (x,y). Якщо аргумент x отримує приріст dx, а аргумент y – приріст dy, то вираз dz=f(x+dx,y+dy)-f(x,y) називають повним приростом функції f(x,y) .
Означення. Функція f(x,y) називається неперервною у точці (x0,y0), якщо
 .
.
Попередні означення легко переносяться із випадку двох змінних на випадок функції від n (n>2) змінних.
Означення. Величини dxz=f(x+dx,y)-f(x,y) та dyz=f(x,y+dy)-f(x,y) називаються частинними приростами функції f(x,y) .
Означення. Частинною (частковою) похідною від функції f(x,y) за аргументом x називається границя
 (6.1)
(6.1)
Частинну (часткова) похідну від функції f(x,y) за аргументом y визначаєють аналогічно.
Для частинних похідних від функції f(x,y) використовують такі позначення :
f¢x(x,y);
z¢x;
![]() ;
;
f¢y(x,y);
z¢y;
![]() .
.
Частинні
похідні
![]() та
та![]() задають
напрями дотичних до поверхні z = f(x,y).
Варто пригадати, що звичайна похідна
f¢(x) =
задають
напрями дотичних до поверхні z = f(x,y).
Варто пригадати, що звичайна похідна
f¢(x) =![]() задає
напрям дотичної до кривої y = f(x).
задає
напрям дотичної до кривої y = f(x).
Приклади
1.
Нехай
![]()
Тоді

![]()
![]()
![]() 2.
Нехай Q=K0.6×L0.4. Знайдемо відповідні
частинні похідні
2.
Нехай Q=K0.6×L0.4. Знайдемо відповідні
частинні похідні


(Випуск продукції зростає зі збільшенням затрат як капіталу, так і праці).
3. Побудуємо другі частинні похідні від функції Q=K0.6×L0.4 .


(Граничний випуск продукції спадає зі збільшенням як затрат капіталу, так і затрат праці).
4. Знайдемо змішані частинні похідні другого порядку :

Теорема: Якщо функція z = f(x,y) та її похідні z¢x , z¢y , z¢¢xy і z¢¢yx неперервні в точці (x,y) та деякому околі цієї точки, то z¢¢xy = z¢¢yx .
Означення. Повним диференціалом dz від функції z =f(x,y) називають суму її частинних диференціалів :
![]() (6.2)
(6.2)
Приклад.
![]()
Тоді
![]()
Поняття повного диференціала має ряд застосувань. По-перше, величина dz є приростом (по z) дотичної площини до поверхні z =f(x,y), аналогічно до того, як диференціал dy від функції f(x) є приростом ординати дотичної до кривої y = f(x) (рис. 6.9,а - б).
Поверхневі інтеграли першого роду:
Означення, властивості, умови існування, обчислення, застосування.






Поверхневі інтеграли другого роду:Означення, властивості, умови існування, обчислення, застосування.



Формула Остроградського- Гауса (зв'язок між поверхневим інтегралом і потрійним).



![]()
Формула Стокса (зв'язок між криволінійним інтегралом другого роду і поверхневим інтегралом).


Векторне поле: означення. Потік векторного поля через поверхню. Дївергенція векторного поля. Теорема Остроградського- Гауса в векторній формі.


Потіквекторного поля через поверхню-поверхневий
інтегралпершого роду поповерхні![]() .
За визначенням
.
За визначенням

де
![]() -
Векторне поле (вектор-функція векторного
аргументу - точки простору),
-
Векторне поле (вектор-функція векторного
аргументу - точки простору),![]() -одиничний
векторпозитивноїнормалідо поверхні (позитивний напрямок
вибирається для ориентируемой поверхні
умовно, але однаково для всіх точок -
тобто для дифференцируемой поверхні -
так, щоб
-одиничний
векторпозитивноїнормалідо поверхні (позитивний напрямок
вибирається для ориентируемой поверхні
умовно, але однаково для всіх точок -
тобто для дифференцируемой поверхні -
так, щоб![]() було
безперервно; для неоріентіруемой
поверхні це не важливо, тому що потік
через неї завжди нуль),
було
безперервно; для неоріентіруемой
поверхні це не важливо, тому що потік
через неї завжди нуль),![]() -
Елемент поверхні.
-
Елемент поверхні.
У тривимірному випадку
 ,
А поверхнею є звичайна двовимірна
поверхню.
,
А поверхнею є звичайна двовимірна
поверхню.
Іноді, особливо у фізиці, застосовується позначення
![]()
тоді потік записується у вигляді
 .
.
Пусть
задано векторное поле
![]()
Определение 3.7.
Дивергенциейилирасходимостью векторного поля![]() называется
скалярная функция, определяемая
равенством:
называется
скалярная функция, определяемая
равенством:

На
этот раз векторное поле
![]() порождает
скалярное полеdiv
порождает
скалярное полеdiv![]() .
.
С учетом понятий дивергенции и потока векторного поля формулу Остроградскогоможно представить в форме:

т.
е. поток векторного поля
![]() через
замкнутую поверхностьSв
направлении внешней нормали равен
тройному интегралу от дивергенции
векторного поля по области, ограниченной
этой поверхностью.
через
замкнутую поверхностьSв
направлении внешней нормали равен
тройному интегралу от дивергенции
векторного поля по области, ограниченной
этой поверхностью.
На
основании формулы (3.38) можно записать:
 и,
переходя к пределу, стягиваяV
в точкуМ(при этом величинаV → 0), имеем:
и,
переходя к пределу, стягиваяV
в точкуМ(при этом величинаV → 0), имеем:

То
есть div![]() есть
предел отношения потока поля
есть
предел отношения потока поля![]() через
бесконечно малую замкнутую поверхность,
окружающую точкуМ, к величине
объёма, ограниченного этой поверхностью.
Из этого следует, что дивергенция не
зависит от выбора системы координат.
через
бесконечно малую замкнутую поверхность,
окружающую точкуМ, к величине
объёма, ограниченного этой поверхностью.
Из этого следует, что дивергенция не
зависит от выбора системы координат.
Если
поток
 ,
то в областьVвтекает большее
количество жидкости (если следовать
ранее рассмотренному примеру о течении
несжимаемой жидкости), чем вытекает из
неё, т.е. внутри областиVимеются
источники жидкости.
,
то в областьVвтекает большее
количество жидкости (если следовать
ранее рассмотренному примеру о течении
несжимаемой жидкости), чем вытекает из
неё, т.е. внутри областиVимеются
источники жидкости.
Если П < 0, то внутри областиVесть стоки. Но поток векторного поля характеризует интенсивность источников и стоков лишь суммарно, т.е. приП ≥ 0внутри областиVмогут быть как источники, так и стоки.
Для
характеристики точки можно использовать
div![]() .
.
Если
div![]() > 0, то данная точка есть
источник, еслиdiv
> 0, то данная точка есть
источник, еслиdiv![]() < 0– то сток.
< 0– то сток.
Заметим,
что div![]() можно
записать с помощью символического
вектора Гамильтона
можно
записать с помощью символического
вектора Гамильтона в
следующем виде:
в
следующем виде:

Отметим свойства дивергенции (справедливость которых рекомендуется показать самостоятельно):
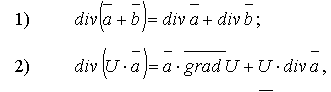
где U– скалярная функция.
