7.1 Ветвление

В данной реализации алгоритма метода ветвей и границ используется правило бинарного ветвления, то есть на каждом шаге задача разбивается на две подзадачи методом добавления двух взаимоисключающих и исчерпывающих все возможности ограничения. Рассмотрим детально этот процесс.

Пусть – целочисленная переменная (), значение которойв оптимальном решении ослабленной задачи является дробным числом. Интервалне содержит допустимых целочисленных компонент решения (гдецелая часть¹ числа ). Потому допустимое решение должно удовлетворять одному из условий:

;	(10)
.	(11)

Ввод этих условий во входную задачу порождает две несвязанные между собой ЗЦЛП: (6)-(9),(10) и (6)-(9),(11) (рисунок 7.3)

Рисунок 7.3 - Ветвление

Говорят, что исходная задача разбивается на две подзадачи. Формально, правило ветвления множества записывается так: еслине целочисленная компонента решенияослабленной задачи, то разбитие множестваследующее:

.

Что касается правила выбора множества для ветвления, то будем выбирать ту вершину дерева, которая имеет наименьшую оценку.

7.2 Вычисление оценки

Пусть имеем ЗЦЛП из множества допустимых решений :

(12)

Задача (12) является задачей, которая соответствует одному из подмножеств , полученному в процессе ветвления. Если, тоявляется правой частью одного из ограничений типа (11), если, тоявляется правой частью одного из ограничений ти­па (10).

Оценочной для задачи (12) является задача линейного программирования:

(13)

Пусть – решение задачи (13). Тогда нижняя оценка решений задачи (12) такая:.

Дерево подмножества решений будем изображать так, как показано на рисунке 7.4.

Рисунок 7.4 – Дерево подмножества решений

Для каждой вершины дерева значение ослабленной задачи дает нижнюю оценку соответствующего множества решений.

7.3 Тест

Предположим, что рекордное решение (наилучшее допустимое, найденное до текущего момента времени) имеет значение целевой функции (рекорд). И пусть в дереве ветвления есть вершина с нижней оценкой:. Это означает, что любое допустимое решениезадачи (6) - (9), которое можно получить в результате разработки этой вершины, будет иметь значение целевой функции. Таким образом, нет смысла разветвлять эту вершину, потому что соответствующее ей подмножество допустимых решений не содержит решений, которые были бы лучше, чем текущее рекордное. То есть эта вершина может быть исключена из рассмотрения.

7.4 Примеры использования метода ветвей и границ для решения задач целочисленного линейного программирования

Пример 1

Решить задачу [1]:

При решении данной ЗЦЛП методом ветвей и границ для получения решений промежуточных ослабленных задач используем графический метод (это позволит не загромождать процесс решения большим объемом вычислений и наглядно продемонстрировать суть метода).

Сначала найдем решение ослабленной задачи (назовем ее задачей 0):

Она имеет нецелочисленное решение (рис. 7): =1,5,=2,5,z=4.

Обе переменные x₁ и x₂ не удовлетворяют условиям целочисленности. По каждой из них можно разбить задачу 0 на две подзадачи. Выберем переменную x₁ (=1,5). Допустимое решение начальной задачи удовлетворяет условию одного из неравенств:

и ,

или и.

Ввод этих условий в начальную задачу порождает две несвязанные между собой ЗЦЛП:

Задача 1

Задача 2

После использования графического способа решения соответствующих задач, рисунок 7.5 получены такие оптимальные решения:

– задача 1: =1,=⁵/₃, z= ⁸/₃;

– задача 2: =2,=⁵/₃, z= ¹¹/₃.

Рисунок 7.5 – Графический способ решения задач (0,1,2)

Это означает, что все допустимые (целочисленные) решения задачи 1 имеют верхнюю оценку =⁸/₃, а задачи 2 - =¹¹/₃. Подмножество решений, которое соответствует задаче 2, имеет оценку лучше. Потому дальнейшее ветвление проведем именно для этого подмножества. В решении задачи 2 переменная x₂ имеет дробное значение (=⁵/₃). Проведем ветвление по этой переменной. Допустимое решение начальной задачи должно удовлетворять условию одного из неравенств:

и ,

или и.

Ввод этих условий в исходную задачу порождает две несвязанные между собой ЗЦЛП:

Задача 3

Задача 4

Решения этих задач показано на рисунке 7.6:

– задача 3: =¹²/₅, =2,z = ¹⁷/₅;

– задача 4 не имеет допустимых решений.

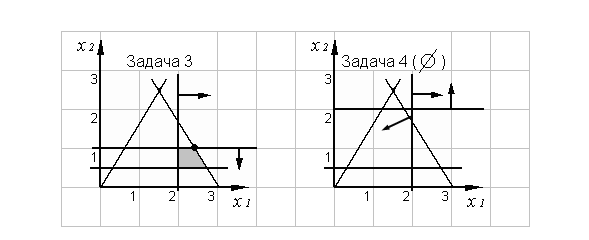
Рисунок 7.6 – Графический способ решения задач (3,4)

Подмножество решений, которое соответствует задаче 3, на текущий момент имеет наилучшую оценку. Потому дальнейшее ветвление проведем для этого подмножества. В решении задачи 3 переменная x₁ имеет дробное значение. Ветвление проведем по этой переменной. Допустимое решение начальной задачи должно удовлетворять условию одного из не­равенств:

и .

Ввод этих условий в исходную задачу порождает две несвязанные между собой ЗЦЛП:

Задача 5

Задача 6

Решение этих задач показано на рисунке 7.7:

– задача 5: = 2,=1,z= 3 - рекордное решение;

– задача 6 не имеет допустимых решений.

Рисунок 7.7 – Графический способ решения задач (5,6)

На основе решения исходной задачи построим дерево поиска решений, которое изображено на рисунке 7.8.

Рекордное решение имеет значение целевой функции =3. Нет смысла разветвлять вершины, которые соответствуют задачам 1 и 3 (соответствующие оценки равны⁸/₃ и ¹⁷/₅), потому что их подмножества допустимых решений не содержат решений, которые были бы лучше, чем текущее рекордное. Таким образом, соответствующие вершины могут быть исключены из рассмотрения. Получили оптимальное решение исходной задачи: x₁=2, x₂=1, значение задачи z=3.

Рисунок 7.8 – Дерево поиска решений

Пример 2

Решить следующую ЗЦЛП.

max z= 3x1+x2;
x1+4x2 16;	(14)
2x1+5x2 13;	(15)
x1, x2 0;	(16)
x1, x2 – целые.	(17)

Задача 0. Решим ослабленную ЗЛП с ограничениями (14)-(16) (то есть без учета ограничений целочисленности (17) ):

max z= 3x1+x2;
x1+4x2 16;
2x1+5x2 13;
x1, x2 0;

Заполним начальную симплекс-таблицу для ослабленной задачи (таблица 7.1).

Таблица 7.1

Б/П	x1	x2	x3	x4	Решение
z	-3	-1	0	0	0
x3	1	4	1	0	16
x4	2	5	0	1	13

Оптимальное решение ослабленной задачи (задачи 0) приведено в таблице 7.2.

Таблица 7.2

Б/П	x1	x2	x3	x4	Решение
z	0	13/2	0	3/2	39/2
x3	0	3/2	1	-1/2	19/2
x1	1	5/2	0	1/2	13/2

Решение не удовлетворяет условиям целочисленности (17) - обе переменные не целые. Выполним ветвление по переменной :(получим соответственно задачу 1 и задачу 2).

Задача 1

max z= 3x1+x2;
x1+4x2 16;	(14а)
2x1+5x2 13;	(15а)
x1, x2 0;	(16а)
x16;	(18)
x1, x2 – целые.

Для учета нового ограничения (18) необходимо выполнить такие действия:

1. ввести остаточную переменную:

   x1+x5 = 6;

   (18а)

2. выразить базисную переменную , которая входит в равенство (18а), через небазисные из соответственной строки оптимальной симплекс-таблицы задачи 0:

x₁= ¹³/₂ - ⁵/₂ x₂ - ¹/₂ x₄;

3. подставить выражение для базисной переменной в (18а):

-⁵/₂x₂ - ¹/₂ x₄+ x₅ =^-1/₂;

4. ввести полученное ограничение в оптимальную симплекс-таблицу задачи 0 и для ослабленной задачи выполнить итерацию двойственного симплекс-метода (Таблица 7.3):

Таблица 7.3

Б/П	x1	x2	x3	x4	x5	Решение
z	0	13/2	0	3/2	0	39/2
x3	0	3/2	1	-1/2	0	19/2
x1	1	5/2	0	1/2	0	13/2
x5	0	-5/2	0	-1/2	1	-1/2
Отно-шение		-13/5		-3
		мин. по мо-ду-лю

Оптимальное решение задачи 1(Таблица 7.4):

Таблица 7.4

Б/П	x1	x2	x3	x4	x5	Решение
z	0	0	0	1/5	13/5	91/5
x3	0	0	1	-4/5	3/5	46/5
x1	1	0	0	0	1	6
x2	0	1	0	1/5	-2/5	1/5

Задача 2.

max z= 3x1+x2;
x1+4x2 16;	(14б)
2x1+5x2 13;	(15б)
x1, x2 0;	(16б)
x17;	(19)
x1, x2 – целые.

Для учета нового ограничения (19) выполним такие действия:

0. ограничения (19) приведем к виду “≤”, помножив его на -1;

Потом для этого ограничения, как и при решении задачи 1, выполняем пунк­ты 1) – 4):

1. -x₁+ x₆ =-7 ;

2. x₁= ¹³/₂ - ⁵/₂ x₂ - ¹/₂ x₄;

3. ⁵/₂ x₂+¹/₂ x₄+x₆ = -¹/₂ ;

4. ввести полученное ограничение в оптимальную симплекс-таблицу задачи 0 и для ослабленной задачи выполнить итерацию двойственного симплекс-метода.

Из последнего равенства видим, что ограничение (19) противоречит ограничениям (14) – (16), т.к. все коэффициенты при переменных левой части равенства положительны, а правая часть равенства отрицательна. Это означает, что задача 2 допустимых решений не имеет.

На этот момент имеем только одно подмножество решений (соответствующее задаче 1). Проведем ветвление задачи 1 по переменной x₂: (получим соответственно задачи 3 и 4).

Задача 3.

max z= 3x1+x2;
x1+4x2 16;	(14в)
2x1+5x2 13;	(15в)
x1, x2 0;	(16в)
x16;	(18а)
x20;	(20)
x1, x2 0;
x1, x2 – целые.

С учетом ограничений неотрицательности переменных (x₂  0) и ограничения (20) (x₂ 0) имеемx₂=0. Задача 3 сводится к задаче оптимизации в пространстве . В этом случае не нужно использовать симплекс-метод.

Задача 4.

max z= 3x1+x2;
x1+4x2 16;	(14г)
2x1+5x2 13;	(15г)
x1, x2 0;	(16г)
x16;	(18б)
x2 1;	(21)
x1, x2 0;
x1, x2 – целые.

Для учета нового ограничения (21), которое запишем в виде - x₂-1, выполним действия, указанные в пунктах 2)-4) ( как и при решении задачи 1):

-x₂ + x₇= -1;

x₂ = -¹/₅x₄+²/₅x₅+¹/₅ (из оптимальной симплекс-таблицы задачи 1) ;

¹/₅ x₄ - ²/₅ x₅ + x₇= - ⁴/₅.

Введем последнее ограничение в оптимальную симплекс-таблицу ослабленной задачи 1(таблица 7.5):

Таблица 7.5

Б/П	x1	x2	x3	x4	x5	x7	Решение
z	0	0	0	1/5	13/5	0	91/5
x3	0	0	1	-4/5	3/5	0	46/5
x1	1	0	0	0	1	0	6
x2	0	1	0	1/5	-2/5	0	1/5
x7	0	0	0	1/5	-2/5	1	-4/5
Отно-шение				–	-13/2

После реализации итерации двойственного симплекс-метода получаем оптимальное решение задачи 4 (Таблица 7.6):

Таблица 7.6

Б/П	x1	x2	x3	x4	x5	x7	Решение
z	0	0	0	3/2	0	13/2	13
x3	0	0	1	-1/2	0	3/2	8
x1	1	0	0	1/2	0	5/2	4
x2	0	1	0	0	0	-1	1
x5	0	0	0	-1/2	1	-5/2	2

Согласно процессу решения исходной задачи построим дерево подмножеств решений (рисунок 7.9). На рисунке 7.10 приведена графическая иллюстрация решения задачи 0, на рисунке 7.11 - иллюстрация решения задач 1 и 2, на рисунке 7.12 – задач 3 и 4.

Таким образом, в результате решения исходной задачи получено два допустимых целочисленных решения:

1)

2)

Оптимальным является первое решение.

Рисунок 7.9 – Дерево подмножеств решений

Рисунок 7.10 – Графическая иллюстрация решения задачи 0

Рисунок 7.11 – Графическая иллюстрация решения задач (1,2)

Рисунок 7.12 – Графическая иллюстрация решения задач (3,4)