47. Сортировка подсчетом

Суть метода заключается в том, что на каждом шаге подсчитывается, в какую позицию результирующего массива B надо записать очередной эле­мент исходного массива A (рис. 40). Если некоторый элемент A[i] помеща­ется в результирующий массив в позицию k + 1, то слева от B[k + 1] долж­ны стоять элементы меньшие или равные B[k + 1]. Значит, число k склады­вается из количества элементов меньших A[i] и, возможно, некоторого числа элементов, равных A[i]. Условимся, что из равных будут учитываться толь­ко те элементы, которые в исходном массиве стоят левее A[i]:

Алгоритм CountingSort(A[1..n],B[1..n])

1. For i=1 to n do C[i]<-0

2. For i=1 to n-1 do

3. For j=i+1 to n do

4. If A[i]>=A[j] then C[i]<-C[i]+1

5. Else C[j]<-C[j]+1

6. End for

7. End for

8. For i=1 to n do

9. B[C[i]+1]<-A[i]

10. Return B

48. Сортировка слиянием. Рекурсивный алгоритм

Этот метод сортирует массив последовательным слиянием пар уже отсортированных подмассивов.

Пусть к - положительное целое число. Разобьем массив А[1]...А[n] на участки длины к. (Первый - А[1]..А[к], затем А[к +1]...А[2 к] и т. д.) Последний участок будет неполным, если п не делится нацело на к. Назовем массив к -упорядоченным, если каждый из этих участков дли­ны к упорядочен.

Ясно, что любой массив 1-упорядочен, так как его участки длиной 1 можно считать упорядоченными. Если массив к -упорядочен и п < к, то он упорядочен.

Рассмотрим процедуру преобразования к -упорядоченного массива в 2 к -упорядоченный. Сгруппируем все участки длины к в пары участков. Теперь пару упорядоченных участков сольем в один упорядоченный участок. Проделав это со всеми парами, получим 2 к -упорядоченный массив

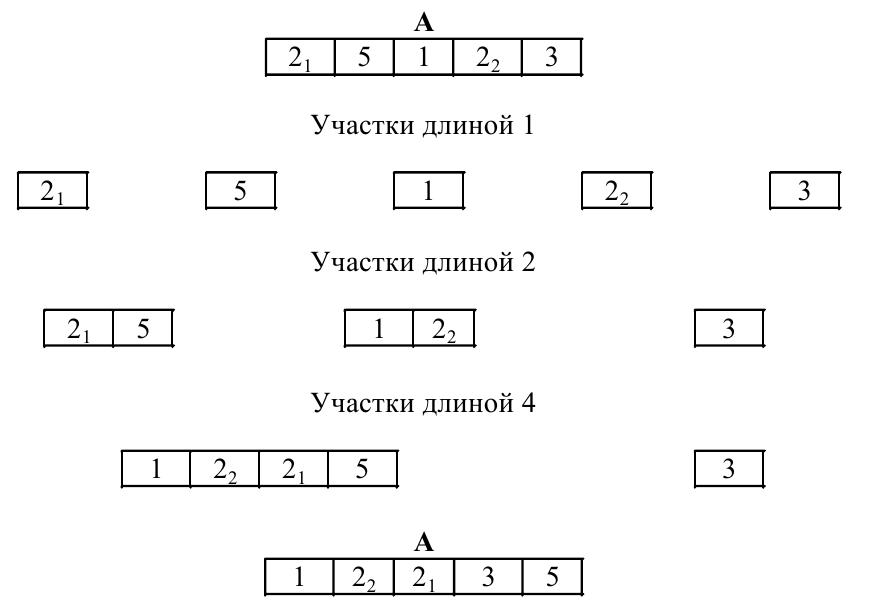
Слияние требует вспомогательного массива B для записи результа­тов слияния. При слиянии сравниваем наименьшие элементы участков рассматриваемой пары, и меньший из них заносим в массив B. Повто­ряем описанные действия до тех пор, пока не исчерпается один из уча­стков. После чего заносим в массив B все оставшиеся элементы другого участка. Затем переходим к следующей паре участков

Сразу же бросается в глаза недостаток алгоритма – он требует допол­нительную память размером порядка n (для хранения вспомогательного массива). Кроме того, он не гарантирует сохранение порядка элементов с одинаковыми значениями. Но его временная сложность всегда про­порциональна O(nlog n) (так как преобразование k-упорядоченного мас­сива в 2k-упорядоченный требует порядка n действий и внешний цикл по k совершает порядка log n итераций).

Алгоритм MergeSort(A[1..n])

1. If n>1 then

2. Копировать A[1..[n/2]] в B[1..[n/2]]

3. Копировать A[[n/2]+1..n] в C

4. MergeSort (B)

5. MergeSort (C)

6. MergeLists(B,C,A)

7. End if

Алгоритм MergeLists(B[1..p].C[1..q],A[1..p+q])

1. i<-1, j<-1, k<-1

2. while (i<p) and (j<q) do

3. if B[i]<=C[j] then A[k]<-B[i]; i<-i+1

4. Else A[k]<-C[j]; j<-j+1

5. K<-k+1

6. End while

7. If (i==p) then копировать C[j..q] в A[k..p+q]

8. Else копировать B[i..p] в A[k..p+q]

9. End if

10. Return A

49. Нижняя граница вычислительной сложности алгоритмов сортировки.

Предложение 1. Функция f (n)=⌈log2 n!⌉ является нижней границей сложности алгоритмов сортировки массивов длины n c помощью сравнений.

(Пример, идет как доказательство!)

Пример 1. Рассмотрим класс алгоритмов сортировки с помощью сравнений. Если алгоритм работает для массивов любой длины, то, разумеется, можно рассмотреть этот алгоритм применительно к массивам некоторой фиксированной длины n. Любая сортировка с помощью сравнений может быть для каждого конкретного n изображена бинарным деревом. В корне и внутренних вершинах находятся выполняемые сравнения, в листьях выписаны результаты сортировки. Априори в исходном массиве возможен любой порядок элементов, поэтому дерево будет иметь n! листьев. Если взять, например, сортировку простыми вставками, то при n = 2 ее можно изобразить деревом, представленным на рис. 1а. При n = 3 дерево принимает вид, показанный на рис. 1б. Сложность в худшем случае для каждого n равна высоте соответствующего дерева (напомним, что высотой листа называется число ребер в том единственном пути, который ведет от корня дерева к этому листу; высотой дерева называется максимум высот его листьев). Если высота некоторого бинарного дерева равна h, то, очевидно, оно содержит не более 2^h листьев (максимальное возможное число листьев достигается в случае полного бинарного дерева, которое имеет ровно 2^h листьев). Поэтому если T(n)—это временная сложность некоторой сортировки сравнениями, то должно выполняться неравенство

2^(T(n))>=n!,

{^ - это знак степени!}

откуда T(n)>=log2 n!; так как значение T(n)—целое число (мы измеряем сложность числом сравнений), то T(n)>=⌈log2 n!⌉ . Доказанное можно сформулировать в виде Предложения 1(см. наверху).

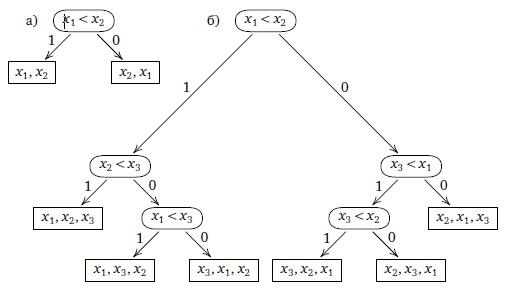
Рис.1 Дерево сортировки простыми вставками для случаев а) n = 2 и б) n =3.