
7
.doc
![]() или
или
![]() (4-54)
(4-54)
При воздействии единичного скачка на средство измерений возникает динамическая погрешность ∆y(t) =h(t)-kномl(t) или ∆x(t)= h(t)-kномl(t). При таком воздействии погрешность ∆х (t) для инерционных средств измерений в момент включения х (t) достигает значения амплитуды скачка х(t), уменьша-
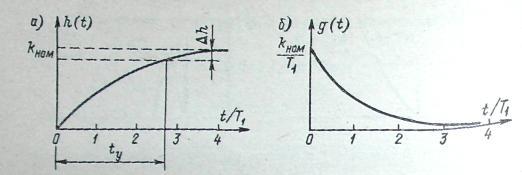
Рис 4-13. Переходная (а) и весовая (б) функции звена первого порядка
ясь со временем в зависимости от динамических свойств средств измерений. Текущее значение динамической погрешности ∆х (t) полностью определяется переходной характеристикой рассматриваемого динамического звена.
Переходная характеристика h (t) звена первого порядка (рис. 4-13, а), определяемая решением уравнения (4-48) при х (t)=1 (t), имеет вид
![]() (4-55)
(4-55)
Импульсная
переходная характеристика g
(t)
=![]() (рис. 4-13, б)
для данного звена
(рис. 4-13, б)
для данного звена
g(t)=![]() (4-56)
(4-56)
Часто для оценки
переходного режима определяют время
установления ty.
Из выражения
(4-55) время установления ty
=
![]() ,
где
,
где
![]() ,
∆h
— допускаемая погрешность установления
выходной величины (см. рис. 4-13, а). Для
некоторых электроизмерительных приборов
за ty
, принимается время, необходимое для
установки указателя на геометрическую
середину шкалы с погрешностью ±1% длины
шкалы, т. е.
,
∆h
— допускаемая погрешность установления
выходной величины (см. рис. 4-13, а). Для
некоторых электроизмерительных приборов
за ty
, принимается время, необходимое для
установки указателя на геометрическую
середину шкалы с погрешностью ±1% длины
шкалы, т. е.
![]() =
1/50. В этом случае ty
=4T1.
=
1/50. В этом случае ty
=4T1.
Для звена второго
порядка вид характеристики h
(t)
и g
(t)
зависит от
![]() (см.
рис. 4-14). Для этого звена рассматривают
три режима:
(см.
рис. 4-14). Для этого звена рассматривают
три режима:
колебательный
режим (![]() <
1)
<
1)
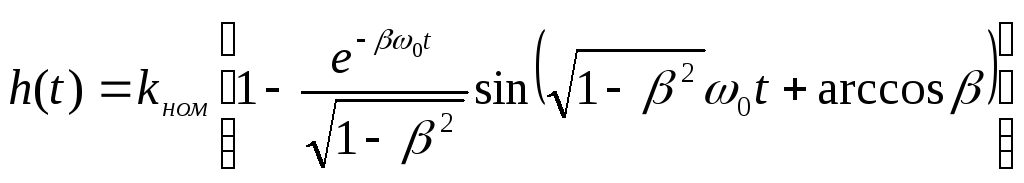 ; (4-57)
; (4-57)
![]() ; (4-68)
; (4-68)

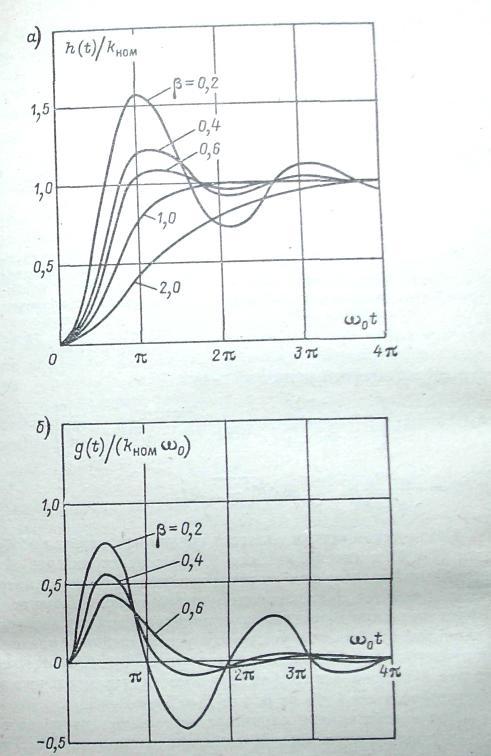
Рис. 4-14. Переходная (а) и весовая (б) функции звена второго порядка
критический режим (β=1)
![]() (4-59)
(4-59)
![]() (4-60)
(4-60)
апериодический режим (β>1)
Рис.
4-16. График зависимости
от β приведенного первого максимального
отклонения от
установившегося значения
для звена второго
порядка
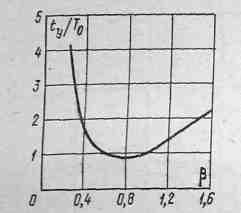
Рис.
4-15. График зависимости
относительного времени установления
выходного
сигнала ty/Tо
от
β для звена
второго порядка
![]() ; (4-61)
; (4-61)
![]() (4
- 62)
(4
- 62)
Критический режим является граничным между колебательным (β<1) и апериодическим (β> 1); он характерен тем, что переходный процесс в таком режиме наиболее быстро и апериодически стремится к установившемуся значению. Однако если время установления определят с рекомендованной для электроизмерительных приборов погрешностью установления (см. звено первого порядка), то минимум ty будет при β=0,8. Для этого случая на рис. 4-15 приведен график зависимости относительного времени установления ty/T0 от β, где То=2π/w0.
При колебательном
характере переходного процесса в ряде
случаев оценивают первое максимальное
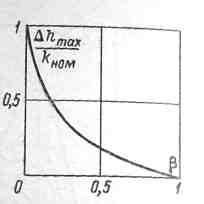
отклонение ∆hmax
выходного сигнала (см. рис. 4-14) от
установившегося значения h(![]() ).
Для этого определяют значение первого
экстремума переходной характеристики
h
(t=t1з)>
где t1з
находят из
условия g(t=t1з)=0.
).
Для этого определяют значение первого
экстремума переходной характеристики
h
(t=t1з)>
где t1з
находят из
условия g(t=t1з)=0.
Из уравнений (4-57) и (4-58) получим
![]() (4-63)
(4-63)
График зависимости ∆hmax/kном приведен иа рис. 4-16.
Частотные
характеристики.
Частотные методы анализа основаны
на исследовании прохождения гармонических
колебаний различных частот через
средства измерений. Если на вход
линейного устройства подать сигнал
X
(jw)
— Хт
(w)
ejwt,
то выходной
сигнал можно записать в виде
У(jw)=Уm(w)ej[wt+t(w)]=![]() .
Отношение
.
Отношение
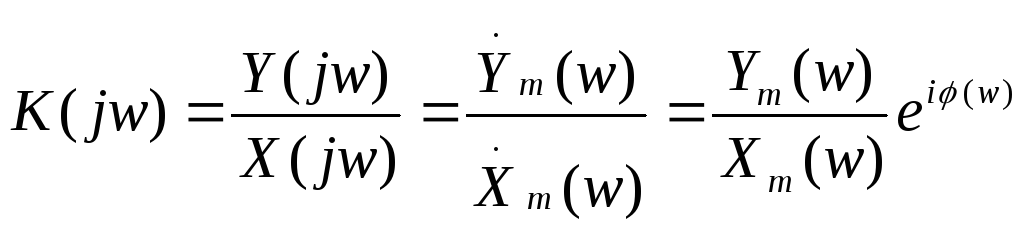 (4-64)
(4-64)
называют амплитудно-фазовой характеристикой. Амплитудно-фазовую характеристику можно получить из дифференциального уравнения (4-44), подставив в него выражения X(jw) и У (jw) и решив полученное уравнение относительно Ym/Xm:
К (jw)=kном/[An(jw)n + An-1(jw)n-1 + …+A1jw +1]. (4-65)
Следует иметь в виду, что У(jw.) представляет собой частное решение дифференциального уравнения и поэтому амплитудно-фазовая характеристика К(jw) непосредственно определяет только установившийся режим.
На практике широкое
распространение получила амплитудно-частотная
характеристика (АЧХ) K(w)
= |K(jw)|=Ym(w)/Xm(w)
и фазово-частотная характеристика (ФЧХ)
—![]() .
.
Из выражения
(4-65) получают выражения К
(jw),
К (w)
-и
![]() для
типовых звеньев.
для
типовых звеньев.
Идеальное безынерционное звено имеет
K(jw)
=kном,
K(w)=kном,
![]() =0. (4-66)
Звено
первого порядка (см. рис. 4-17)
=0. (4-66)
Звено
первого порядка (см. рис. 4-17)
K(jw)=kном/(1+jwT1); (4-67)
K(w)
= kH0M/![]() ; (4-68)
; (4-68)
![]() =
- arctgwT1. (4-69)
=
- arctgwT1. (4-69)
Звено второго порядка (см. рис. 4-18)
K(jw)=kном/ (1 - w2/w02+j2βw/w0) ; (4-70)
К (w)
=kном/![]() (4-71)
(4-71)
![]() =-
arctg
=-
arctg![]() (4-72)
(4-72)
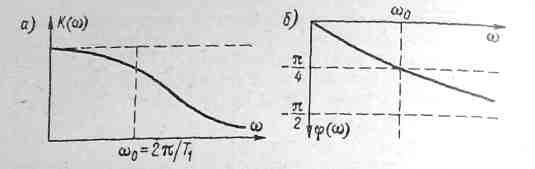
Рис. 4-17. Амплитудно-частотная (а) и фазово-частотная (б) характеристики звена первого порядка
Для звена второго порядка вид АЧХ и Ф-ЧХ существенно зависит от степени успокоения β, При β=0,6-0,7 в относительно широком диапазоне частот (см. рис. 4-18) К (w) ≈ kном. Этот режим важен для многих практических применений средств измерений. При β<0,6 наблюдаются резонансные явления для частот w, близких к w0.
Ясная физическая интерпретация и относительная простота экспериментального определения послужили причиной широкого применения частотных характеристик в измерительной технике.
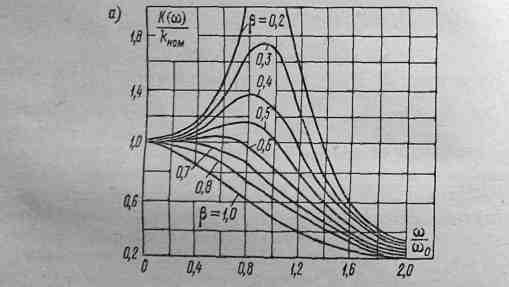 Рис.
4-18. Амплитудно-частотная (а) и
фазово-частотная (б) характеристики
звена второго порядка.
Рис.
4-18. Амплитудно-частотная (а) и
фазово-частотная (б) характеристики
звена второго порядка.
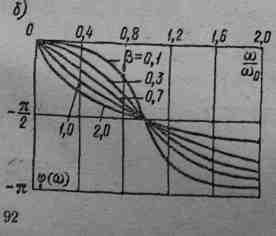
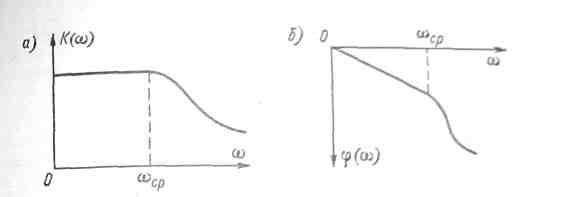

Рис 4.19. Амплитудно-частотная (а) и фазово-частотyая (б) характеристики некоторого средства измерений
Рассмотрим
возможность оценки динамических
погрешностей по известным АЧХ и ФЧХ
средств измерений для сигнала х
(t),
заданного диапазоном изменения от —хт
до +хm
и частотным
диапазоном 0—wm.
Предположим, что средство измерений
имеет такие АЧХ и ФЧХ, как показано на
рис. 4-19. Для частот О
—wСр
характеристики K(w)
= kном,
![]() ,
где t3=const
— время
задержки выходного сигнала. Частоту
wср
называют частотой среза (на практике
К (w)≈kном
с некоторой заданной погрешностью)
. Для частот w
> wср
характеристика К
(w)
≠ kH0M,
а φ (w)
имеет нелинейную зависимость от частоты.
,
где t3=const
— время
задержки выходного сигнала. Частоту
wср
называют частотой среза (на практике
К (w)≈kном
с некоторой заданной погрешностью)
. Для частот w
> wср
характеристика К
(w)
≠ kH0M,
а φ (w)
имеет нелинейную зависимость от частоты.
Сначала оценим влияние на динамическую погрешность только АЧХ. Для этого условно примем φ(w) =0. При wт<wср, очевидно, погрешность не возникает, так как каждая гармоническая составляющая передается с одним и тем же коэффициентом kном; при wm> wср они передаются с К (w) ≠kном, что приводит к искажению y(t), а следовательно, и появлению погрешности. Для каждой гармонической составляющей xi (t) =Xmi sin wit относительная погрешность
σAi= [XmiK(wi)—Xmi kном]/ (Xmi kном) =[K(wi)-kном]/kном (4-73)
где K(wi) — значение АЧХ на частоте wi (. Можно показать, что для полигармонического сигнала при условии \х(t)|≤ хm максимальная приведенная погрешность будет определяться выражением
max yA ≤ max [К (w≤wm) –kном]/kном, (4-74)
где max [К (w≤wm) — kном]—максимальная разность коэффициентов передачи в пределах диапазона частот 0—wm, определяемая по АЧХ средства измерений.
. Теперь рассмотрим влияние ФЧХ на результаты измерений. Примем условно К(w)=kном во всем диапазоне рассматривае-
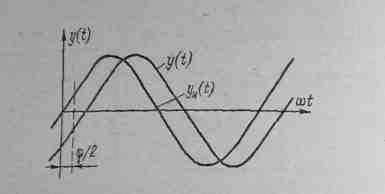
Рис. 4-20. Выходные сигналы реального у (t) и идеального yи (t) средства измерений
мых частот. При х (t) =Хт sinwt имеем уи (t) =kном Хт sin wt, 'y{f)=kном Xmsin(wt+φ). В тех случаях, когда требуется «жесткая привязка» результатов измерений во времени, возникает погрешность ∆y(t)=y(t)-yи(t) вызванная фазовым сдвигом.
Из рис. 4-20 видно, что при φ<π эта погрешность максимальна
при wt=φ/2;
max|∆y(t)|=2kyjv Xmsin φ/2. (4-75)
Если X(t)
представляет собой сумму N
гармонических
Xi(t)
![]() ≤Xm,
то максимально возможная погрешность
≤Xm,
то максимально возможная погрешность
max
\∆у
(t)|![]()
![]()
где max|φi|— максимальный фазовый сдвиг в диапазоне частот 0—wm, определяемый по ФЧХ. Отсюда максимальная приведенная погрешность
maxYи=max|∆y(t)|/(2kномXm)≤sin[max|φi|/2] (4-76)
В некоторых измерительных задачах задержка выходного сигнала во времени несущественна или она может быть учтена в процессе обработки результатов измерений. Важной в таких задачах является точная передача формы сигнала. Так, если сместить сигнал у (t) (см. ряс. 4-20), точно отражающий характер изменения х (t), на время t3=φ/w то он полностью совпадает с сигналом уn(t) в этом смысле погрешность будет отсутствовать. Для сложного сигнала с диапазоном частот 0—wm, лежащим в пределах линейной фазовой характеристики φ(w)=t3w и, возникает аналогичная картина, поскольку каждая гармо-
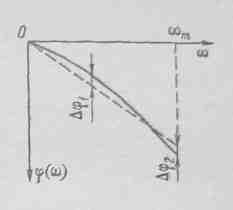
Рис. 4-21- Аппроксимация фазово-частотной характеристики линейной зависимостью
ническая составляющая смещается во времени на постоянную величину t3 В этом случае считают, что динамическая погрешность равна нулю. Если фазовая характеристика нелинейна, то гармонические составляющие смещаются на различное время задержки t3i = φ(wi)/wi, что приводит к искажению формы выходного сигнала, а следовательно, смещение в этом случае не исключает погрешности. Определить эту погрешность в общем 'случае достаточно сложно. Приближенно ее можно оценить, проводя некоторую линейную ФЧХ, аппроксимирующую реальную ФЧХ (рис. 4-21) с максимальными погрешностями ∆φ1=∆φ2=∆φ. Такая ФЧХ будет соответствовать сдвигу сигнала на некоторое время, определяемое ее наклоном. Оценить погрешность, вызванную нелинейностью ФЧХ измерительного звена, можно по формуле (4-76), подставляя в нее ∆φ вместо max {φi}.
В общем случае на динамическую погрешность влияет как АЧХ, так и ФЧХ измерительного звена. Точное определение суммарной погрешности является относительно сложной задачей. В качестве оценки сверху для общей динамической погрешности может быть принята сумма этих двух составляющих. Однако следует иметь в виду, что данная оценка является достаточно «грубой», поскольку во многих случаях общая погрешность принципиально меньше суммы рассматриваемых составляющих. Так, при моногармоническом сигнале максимальные значения этих составляющих всегда разнесены во времени и, следовательно, общая погрешность будет меньше суммы их максимальных значений.
Передаточные функции. Используя преобразование Лапласа, эапишем уравнение (4-39) в операторной форме
(Anpn+An-1pn-1 + ...+Alp+1) У(р)=kномX(p), (4-77)
рде X (p),Y (р) — изображения по Лапласу x(t), у(t). Отношение изображений выходного и входного сигналов
K(p)=Y(p)/X (р) =kном/(Anpn+An-1pn-1+…+A1p+1) (4-78)
называют передаточной функцией. Передаточная функция является полной математической моделью средства измерений. При известном входном сигнале х (t) и его изображениях X(р) изображение выходного сигнала определяется из соотношения У(р)=К(р)Х[р). (4-79)
Передаточную функцию (4-78) можно представить в виде произведения
K(p)
=![]() .
где pi
—корни знаменателя выражения (4-78). Такая
форма записи
имеет известную физическую интерпретацию:
сложное средство измерений с передаточной
функцией типа (4-78) может быть представлено
последовательным соединением простейших
звеньев.
Такие звенья имеют следующие передаточные
функции: идеальное
звено
.
где pi
—корни знаменателя выражения (4-78). Такая
форма записи
имеет известную физическую интерпретацию:
сложное средство измерений с передаточной
функцией типа (4-78) может быть представлено
последовательным соединением простейших
звеньев.
Такие звенья имеют следующие передаточные
функции: идеальное
звено
К (p)=kном; (4-80)
звено первого порядка K(p)=kном/(TiP+1); (4-81)
звено
второго порядка К
(Р)
=kном/(р2/w2+2![]() (4-82)
(4-82)
Динамические свойства таких звеньев, как было показано выше, хорошо изучены. При известных сведениях о входных сигналах — диапазоне изменения сигнала, частотном диапазоне, форме сигнала (например, прямоугольные импульсы) и других — для таких звеньев могут быть оценены динамические погрешности. Следует подчеркнуть, что при анализе динамического режима средств измерений чаще всего определяют некоторые оценки динамической погрешности при ограничениях на входные сигналы. Это объясняется тем, что точное решение в общем виде основной измерительной задачи — нахождение х(t) по наблюдаемому сигналу у(t) — наталкивается на серьезные математические трудности. Так, формальная запись уравнения (4-79) в виде x{p)=Y (р)/К (р) приводит к необходимости решения так называемых некорректно поставленных обратных задач. Дело в том, что передаточная функция К*(р) = 1/К(р) описывает принципиально неустойчивое динамическое звено. Вследствие этого небольшим погрешностям исходных данных, а у (t) всегда определяется с некоторой погрешностью, могут соответствовать настолько большие погрешности решения, что последние оказываются лишенными физического смысла. В настоящее время используют специальные методы решения таких задач — методы регуляризации. Эффективность этих методов существенно зависит от характера и объема априорной информации об исходном решении.
Подводя итоги рассмотрению динамического режима средств измерений, отметим следующее. При измерении переменных во времени величин х(t) в реальных средствах измерений возникает динамическая погрешность. Эта погрешность определяется динамическими свойствами средств измерений и характером изменения внешних воздействий (см. § 2-1).
Динамические свойства средств измерений могут быть описаны полными динамическими характеристиками: дифференциальными уравнениями, переходными характеристиками, частотными характеристиками, передаточными функциями, а также частными динамическими характеристиками: временем установления ty (временем реакции), постоянной времени T1, частотой собственных колебаний w0, коэффициентом демпфирования (затухания) β и некоторыми другими.
