
5 Дифференциальное исчисление
.pdf
Производная функции
•Производная функции, заданной параметрически.
•Теорема.
Пусть
1. x (t),
y (t), t t1,t2 ;
2. (t) непрерывная ,
монотонная на t1,t2 ;
3. (t0 ), t0 t1,t2 ,
(t0 ) 0 ;
4. (t) непрерывная на t1,t2 ;
5. (t0 )
Вточке x0 (to )
y (x0 ) (t0 )
(t0 )

Производная функции
•Производные высших порядков.
•Определение 1.
Производная f (x)y
называется производной
первого порядка функции y f (x)
•Определение 2.
Производная от производной первого порядка
называется производной второго порядка
функции y f (x) : y ( f (x))
•Определение 3.
Производная от производной |
(n-1) -порядка |
||||
называется производной |
n – порядка |
|
|||
функции |
y f (x) : y |
(n) |
( f |
(n 1) |
|
|
|
|
(x)) |
||
Пример. |
|
y a x |
y a x ln a ; |
|
y a x (ln a)2 ; |
y(n) a x (ln a)n
Исследование функций
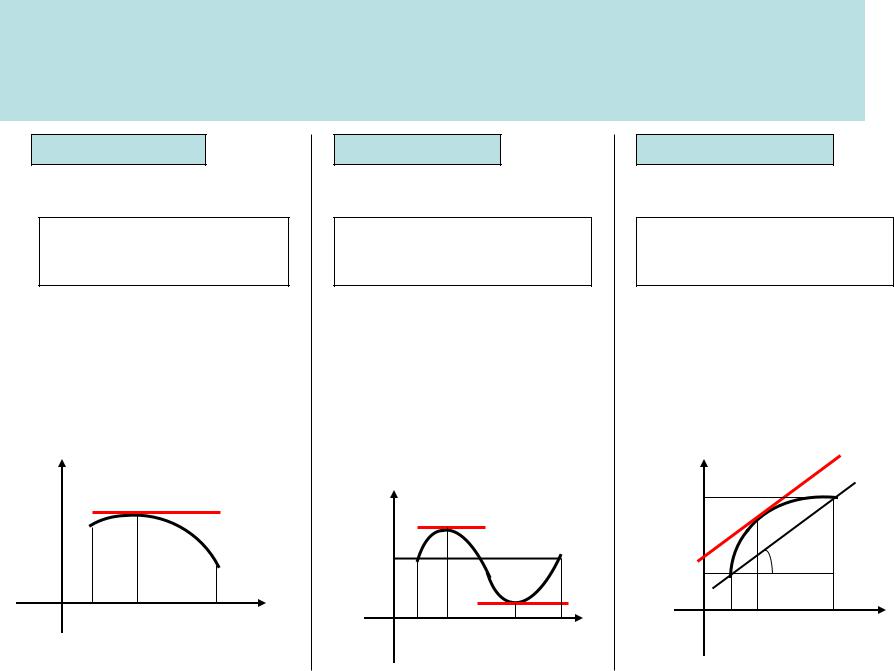
Теорема Ферма.
Пусть функция y f (x) удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или наименьшее значение
во внутренней точке c є (a,b).
|
|
Тогда : |
f (c) 0 |
|
|
|
|
Геометрический смысл.
y
y f (x)
|
|
|
|
|
0 |
a |
c |
b |
x |
Теорема Ролля.
Пусть функция y f (x) удовлетворяет условиям:
а) непрерывна на отрезке [a,b]; б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения f (a) f (b)
Тогда : |
f |
|
|
|
(c) 0 |
|
|
||
хотя бы в одной внутренней |
||||
точке c є (a,b). |
|
|
||
Геометрический смысл. |
|
|||
y |
|
|
|
|
|
|
|
y |
f (x) |
|
|
|
||
f (a) f (b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
a |
c |
c1 |
b x |
|
||||
Теорема Лагранжа.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b]; б) имеет производную f (x)
во всех внутренних точках (a,b);
|
|
f (b) f (a) |
||
Тогда : |
f (c) |
|
|
|
b a |
||||
|
|
|||
хотя бы в одной внутренней
точке c є (a,b).
Геометрический смысл. y
f (b) |
|
|
y f (x) |
|
|
|
f (a) |
|
|
|
|
|
0 a c |
b |
x |

Исследование функций
•Монотонность функции.
–Определение 1.
Функция y f (x) называется
возрастающей в (a,b) , если
x1, x2 (a,b) : x1 x2 f (x1) f (x2 ).
–Определение 2.
Функция y f (x) называется
убывающей в (a,b) , если
x1, x2 (a,b) : x1 x2 f (x1) f (x2 ).
y
f (x2 ) f (x1)
0
y
f (x1) f (x2 )
0
y f (x)
|
|
|
|
|
|
|
|
|
|
a |
x1 |
x2 |
|
b x |
|
|
y f (x) |
||
|
|
|
|
|
a |
x1 |
x2 |
b |
x |
|
|
|
|
|

Исследование функций
•Теорема.
|
f (x) |
x (a,b) . |
Пусть |
|
|
Тогда:
1) f (x) 0 f (x) возрастает в (a,b) ; 2) f (x) 0 f (x) убывает в (a,b) .
•Доказательство.
1. |
x1, x2 (a,b) : x1 x2 |
|
|
|
||
|
|
|
|
|
|
|
|
f (x2 ) f (x1 ) f (c)(x2 x1 ) ; c (x1, x2 ) (a,b). |
|||||
2. |
|
x (a,b) |
|
|
|
|
|
f (x) 0 |
f (c) 0 |
||||
|
f (x2 ) f (x1 ) 0 |
f (x2 ) f (x1 ) |
( убывает) . |
|||
3. |
|
x (a,b) |
|
|
|
|
|
||||||
|
f (x) 0 |
f (c) 0 |
||||
|
f (x2 ) f |
(x1 ) 0 |
f (x2 ) f (x1 ) |
(возрастает) . |
||
Исследование функций
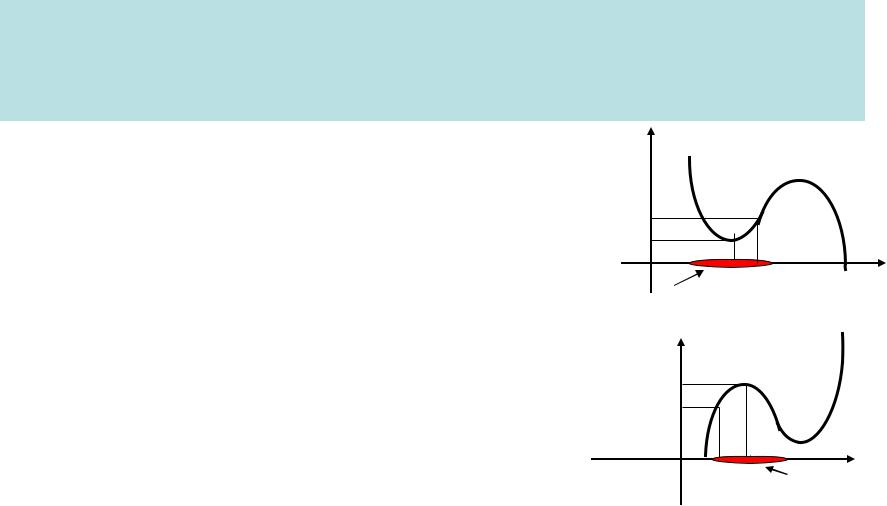
• Экстремум функции.
– Определение 1.
Точка x0 оси ОХ называется
точкой minimum`а функции y f (x),
если - окрестность точки x0 такая, что
f (x) f (x0 ) x окрестности , x x0
– Определение 2. |
|
Точка |
x0 оси ОХ называется |
точкой maximum`а функции y f (x) , |
|
если |
- окрестность точки x0 такая, что |
f (x) f (x0 ) x окрестности , x x0
–Определение 3.
Точками экстремума называются точки minimum`а и точки maximum`а.
Значения функции в этих точках Называют экстремальными значениями.
y
f (x) |
|
f (x0 ) |
|
0 |
x0 x |
|
окрестность |
y
f (x0 )
f (x)
x
0 x0
x
x
окрестность

Исследование функций
• Необходимый признак экстремума.
– Теорема.
1. y f (x) определена |
|
|
в окрестности точки x0 |
|
|
|
f (x0 ) 0 либо |
|
( включая точку x ) |
|
|
0 |
|
f (x0 ) не существует |
2. точка x0 точка экстремума. |
|
|
|
|
–Доказательство.
Пусть f (x0 )  y f (x) - удовлетворяет теореме Ферма
y f (x) - удовлетворяет теореме Ферма  f (x0 ) 0
f (x0 ) 0
–Определение 3.
Критическими точками называются точки оси ОХ, в которых либо f (x) не существует.
f (x) 0

Исследование функций
•Достаточные признаки экстремума.
Определение.
Пусть y f (x) определена и непрерывна
в δ - окрестности точки x0 |
(включая точку x0 |
). |
|||
Пусть f (x) |
в δ - окрестности точки x0 |
|
|
||
(за исключением, быть может, точки x0 ). |
|
|
|||
Говорят, что f (x) при переходе через точку |
|
x |
|||
|
|
|
|
|
0 |
меняет знак с « + » на « - », если |
|
|
|||
при x x0 : |
|
|
при x x0 : |
f |
|
f (x) 0 , |
(x) 0 . |
||||
Говорят, что f (x) |
при переходе через точку |
|
x0 |
||
меняет знак с « - » |
на « + » , если |
|
|
||
при x x0 : |
|
|
при x x0 : |
f |
|
f (x) 0 , |
(x) 0 . |
||||
Исследование функций
•Первый достаточный признак экстремума.
Теорема.
1.y f (x) определена
вокрестности точки x0 (включая точку x0 ) ;
2.точка x0 критическая ;
3.f (x) при переходе через точку x0
меняет знак с « + » на « - »
4. f (x) при переходе через точку x0
меняет знак с « -
Доказательство.
1.f (x) меняет знак
с«+» на «-»
2.f (x) меняет знак
с«-» на «+»
» на « + »
при x x0 :
при x x0 :
при x x0
при x x0
Точка x0 - точка maximum`а
Точка x0 - точка minimum`а
f (x) 0 f (x) возрастает
f(x) 0 f (x) убывает
:f (x) 0 f (x) убывает
:f (x) 0 f (x) возрастает
f (x) f (x0 ) x0 точка max
f (x) f (x0 ) x0 точка min

Исследование функций
•Второй достаточный признак экстремума.
Теорема.
1.y f (x) определена
вокрестности точки x0 (включая точку x0 ) ;
2.f (x0 ) 0 ;
3.f (x0 ) 0 
 Точка x0 - точка minimum`а
Точка x0 - точка minimum`а
4. |
f |
|
|
|
Точка x0 - точка maximum`а |
||||
|
(x0 ) 0 |
