umk_po_TW

ВВЕДЕНИЕ

Теория вероятностей являются важной частью математического образования выпускника любого технического университета. Вероятностные методы широко применяются при решении большого числа инженерных, экономических, финансовых, естественно - научных задач.

Практикум содержит минимальный объем сведений по основным разделам теории вероятностей, типовые примеры с решениями, задачи для самостоятельного решения, контрольные вопросы по теоретической части курса.

Практикум позволяет изучать теорию вероятностей в соответствии с требованиями образовательных стандартов и учебных программ. Он предназначен для студентов второго курса дневного отделения инженерно-технологического факультета.

Рекомендуемая литература:

1.Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман.

— М.: Высшая школа, 1972. — 386 с.

2.Мацкевич, И.П. Сборник задач и упражнений по высшей математике: Теория вероятностей и математическая статистика / И.П. Мацкевич, Г.П. Свирид, Г.М. Булдык. — Минск: Вышэйшая школа, 1996. — 318 с.

3.Сборник индивидуальных заданий по теории вероятностей и математической статистике / А.П. Рябушко [и др.]; под общ. ред. А.П. Рябушко. — Минск: Вышэйшая школа, 1992. — 191 с.

4.Гурский, Е.И. Сборник задач по теории вероятностей и математической статистике / Е.И. Гурский. — Минск: Вышэйшая школа, 1975. — 272 с.

5.Гусак, А.А. Справочник по высшей математике / А.А. Гусак, А.М. Гусак. — Минск: Навука i тэхнiка, 1991. — 480 с.

6.Лихолетов И.И., Мицкевич И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. Мн.: Вышэйшая школа, - 1976.

2

Раздел 1. Случайные события

Тема 1: Элементы комбинаторики

Комбинаторика - раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечного множества.

Размещениями из n элементов по k (0 < k ≤ n) элементов называются со- единения, каждое из которых состоит изk элементов, взятых из данных n эле- ментов. При этом размещения отличаются друг от друга как самими элемента- ми, так и их порядком.

ния, каждое из которых состоит из k элементов, взятых из данных n элементов. Эти соединения отличаются друг от друга хотя бы одним элементом. В отличие от разме- щений, порядок следования элементов здесь не учитывается.

Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами умножения и сложения.

Правило умножения: если из некоторого конечного множества первый объект (элемент x ) можно выбрать n1 способами и после каждого такого выбора второй объ- ект (элемент y ) можно выбрать n2 способами, то оба объекта ( x и y ) в указанном

3

порядке можно выбрать n1 n2 способами.

Этот принцип, очевидно, распространяется на случай трех и более объектов. Пример 4. Сколько трехзначных чисел можно составить из цифр 1, 2,3,4,5, если: а)

цифры не повторяются? б) цифры могут повторятся?

Решение. Имеется 5 различных способов выбора цифры для первого места (слева в трехзначном числе). После того как первое место занято, например, цифрой 2, осталось четыре цифры для заполнения второго места. Для заполнения третьего места остается выбор из трех цифр. Следовательно, согласно правилу умножения имеется 5 . 4 . 3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, ...) Понятно, что если цифры могут повторяться, то трехзначных чисел 5 . 5 . 5 = 125. (Вот некоторые из них: 255, 333, 414, 111, ... )

Правило суммы. Если некоторый объект x можно выбрать n1 способами, а объ- ект y можно выбрать n2 способами, причем первые и вторые способы не пересекаются,

то любой из указанных объектов ( x или y ), можно выбрать n1 + n2 способами.

Пример 5. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

Решение. По правилу умножения двух девушек можно выбрать 14·13 = 182 способами, а двух юношей - 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студенток или двух юношей. Согласно правилу сложения таких способов выбора будет 182 + 30 = 212 .

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1.Сколькими способами можно расставить на полке 5 различных книг?

2.Сколько «слов» по две буквы можно составить из букв a, b, c, d, e, таким образом, чтобы буквы в «словах» не повторялись?

3.Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых из вазы, в которой стоят 10 красных и 4 розовых гвоздики?

4.Сколькими способами могут восемь человек стать в очередь к театральной кассе?

5.Позывные радиостанции должны начинаться с буквы W. 1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из трех букв, причем эти буквы могут повторяться? 2) Если позывные состоят из четырех букв, которые не повторяются?

6.В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?

7.Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?

8.Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять:

9.Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, а) если первая из них не равна нулю; б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?

10.Сколькими способами можно расставить на полке семь книг, если (а) две определенные книги должны всегда стоять рядом, (б) эти две книги не должны стоять рядом?

11.Сколько пятибуквенных слов, каждое из которых состоит из трех согласных и двух гласных, можно, образовать из букв слова уравнение?

Ответы: 1. 120. 2. 20. 3. 60. 4. P8 = 8!. 5. 1) 262; 2) 25 × 24 × 23 . 6. 3× P6 = 3 × 6!. 7. 300. 8.

P8, А87 , А83 . 9. 9 A104 , 26 A94 . 10. 1440; 7!−2 6! . 11. C33C42 P5

Домашнее задание.

1. Расписание одного дня содержит 5 уроков по разным предметам. Определить количество таких расписаний при выборе из 11 предметов.

4

События называются несовместными, если их одновременное появление невоз-

можно при данном испытании, т.е. появление события A в данном испытании исключает появление события B в этом же испытании. Например, если из урны с черными и белыми шарами случайным образом извлекается шар черного цвета, то его появление исключает извлечение белого шара в этой же попытке.

События называются равновозможными, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие. Например, появление герба и появление решки при бросании монеты есть события равновозможные.

Если событие A - какое-либо событие, то событие, состоящее в том, что собы-

тие A не наступило, называется противоположным событию A и обозначается как A . Пример 2. Набирая номер телефона, абонент забыл последние 3 цифры, и помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что номер те-

лефона набран правильно.

Решение. Благоприятствующий исход здесь один – правильный набор последних цифр (m = 1). Всех возможных исходов здесь будет столько, сколько можно составить

Пример 3. Среди 100 колес 5 нестандартных. Для контроля выбирается 7 колес. Найти вероятность того, что среди них ровно 3 будет нестандартных.

Решение. Число всевозможных исходов равно количеству комбинаций из 100 колес по 7 штук, т.к. порядок значения не имеет, то n = C1007 . Благоприятствующий исход состоит в выборе ровно 3 нестандартных колес из 5 и совместном выборе (7-3) стандартных колес из (100-5), порядок значения не имеет. По правилу произведения m = C53 C954 .

Следовательно, вероятность того, что среди взятых для контроля колес будет ровно 3 нестандартных (событие A ):

Относительной частотой события A в данной серии опытов называется отноше-

ние числа опытов, в которых появилось событие A, к общему числу произведенных опы-

тов.

Частоту события часто называют его статистической вероятностью (в отличие от ранее введенной «математической» вероятности).

Частота события вычисляется на основании результатов опыта по формуле

где m – число появления события A; n – общее число произведенных опытов. Пример 4. По цели произвели 24 выстрела, причем было зарегистрировано 19 по-

паданий. Относительная частота поражения цели W ( A) = 19 24

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1.На 5 одинаковых карточках написаны буквы Б, Е, Р, С, Т. Эти карточки наудачу разложены в ряд. Какова вероятность того, что получится слово БРЕСТ?

2.В ящике 4 голубых и 5 красных шаров. Из ящика наугад вынимают 2 шара. Найдите вероятность того, что эти шары разного цвета.

3.В бригаде 4 женщины и 3 мужчин. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?

4.В ящике 10 шаров, из которых 2 белых, 3 красных и 5 голубых. Наудачу извлечены 3 шара. Найдите вероятность того, что все 3 шара разного цвета.

6

во МИНСК?

Ответы: 1. 1 120 . 2. 59 . 3. 35 . 4. 0,25. 5. 1 60 . 6. 21 40 . 7. 59 . 8. 0,81. 9. 1 360 . 10.

1 65 . 11. 1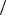4 . 12. 1645 . 13. 0,05. 14. 102 попадания. 15.

Домашнее задание.

1.Сколько различных пятизначных чисел, делящихся на 10 можно составить из цифр 0, 1, 2, 3, 4? Каждую цифру можно использовать в записи только один раз.

2.Из 4 второкурсников, 5 третьекурсников и 6 пятикурсников надо выбрать трех студентов на конференцию. Сколькими способами можно осуществить этот выбор, если среди выбранных должны быть студенты разных курсов?

3.На предприятии имеется 36 строительно-дорожных машин и автобусов в одинаковом количестве. Сколькими способами можно выбрать один автобус и одну машину?

4.10 работников цеха подали заявление на отпуск. Найти вероятность для каждого из них пойти в отпуск первым.

5.В оружейной из 53 пистолетов 35 пистолеты марки «Макарова». Для учений было выдано 42 пистолета. Найти вероятность, что будут среди выданных окажется 30 пистолетов марки «Макарова»?

Тема 3. Сложение и умножение вероятностей

Суммой событий А и В называется событие А + В состоящее в наступлении хо-

тя бы одно из событий: А или В.

Теорема о сложении вероятностей 1. Вероятность появления одного из двух не- совместных событий равна сумме вероятностей этих событий.

Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

P( A1 + A2 + ... + An ) = P( A1 ) + P( A2 ) + ... + P( An )

Если случайные события A1 , A2 , …, An образуют полную группу несовместных событий, то имеет место равенство

P( A1 ) + P( A2 ) + ... + P( An ) = 1

Произведением событий А и В называется событие АВсостоящее в их совмест- ном наступлении, т.е. когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы двух совместных со-

бытий вычисляется по формуле

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых

событий А и В вычисляется по формуле:

Вероятность произведения зависимых событий вычисляется по формуле условной вероятности

P( A B) = P( A) PA (B) или P( A B) = P(B) PB ( A) (3.4)

Пример 1. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика: P( A) = 1 ; 6

8

A - вынули черный шар из первого ящика: P( A) = 5 ;

Тогда искомая вероятность по теореме сложения будет

P = P( AB + AB) = 11 . 18

Пример 2. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка, P( A) = 0,8 ; В – попадание второго стрелка, P(B) = 0,9 .

Тогда A - промах первого, P( A) = 1 − 0,8 = 0,2 ;

B - промах второго, P(B) = 1 − 0,9 = 0,1 .

Найдем нужные вероятности. а) АВ – двойное попадание,

P( AB) = P( A)P(B) = 0,8 0,9 = 0,72

б) AB – двойной промах,

P( AB) = P( A)P(B) = 0,2 0,1 = 0,02 .

в) А+В – хотя бы одно попадание,

P( A + B) = P( A) + P(B) − P( AB) = 0,8 + 0,9 − 0,72 = 0,98

г) AB + AB – только одно попадание,

P( AB + AB) = P( AB) + P( AB) = 0,8 0,1 + 0,2 0,9 = 0,28

Пример 3. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике; В – формула содержится во втором справочнике; С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1)P( ABC + ABC + ABC) = P( ABC) + P( ABC ) + P( ABC) =

=0,6 0,3 0,2 + 0,4 0,7 0,2 + 0,4 0,3 0,8 = 0,188

2)P( ABC + ABC + ABC ) =

=0,6 0,7 0,2 + 0,6 0,3 0,8 + 0,4 0,7 0,8 = 0,452

3)P( ABC) = 0,6 0,7 0,8 = 0,336

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Вероятность того, что наступит хотя бы одно из этих событий, например, если в результате испытания могут появиться три собы-

9

тия, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий, можно найти используя следующую теорему.

Теорема. Вероятность появления хотя бы одного из событий A1 , A2 , …, An , неза-

висимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

Если события A1 , A2 , …, An имеют одинаковую вероятность p , то формула принимает простой вид:

P( A) = 1 − (1 − p)n = 1 − q n

Пример 4. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9 . Найти вероятность хотя бы одного попадания (событие А) при

одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A1 (попадание первого орудия), A2 (попадание второго орудия) и A3 (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям A1 , A2 и A3 (т. е. вероятности

P( A) = 1 − q1q2 q3 = 1 − 0,2 0,3 0,1 = 0,994 .

Пример 5. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События "машина работает" и "машина не работает" (в данный момент)

— противоположные, поэтому сумма их вероятностей равна единице: p + q = 1

Отсюда вероятность того, что машина в данный момент не работает, рав-

наq = 1 − p = 1 − 0,9 = 0,1

Искомая вероятность P( A) = 1 − q 4 = 1 − 0,14 = 0,9999

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1.Два стрелка производят по мишени по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,6, для второго - 0,8. Найти вероятность того, что оба стрелка попадут в мишень.

2.Вероятность боя стеклянной тары при погрузке на автомашины равна 0,06, а при транспортировке на автомашинах - 0,05. Какова вероятность боя стеклянной тары?

3.Вероятность брака из-за нарушения режима обработки деталей равна 0,02, а вследствие неисправности станка - 0,08. Какова вероятность выпуска бракованной детали?

4.Два стрелка производят по мишени по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,6, для второго - 0,8. Найти вероятность того, что: а)

вмишень попадет только один стрелок, б) по крайней мере, один стрелок попадет в мишень.

5.Три стрелка производят выстрел по цели. Вероятность попадания в цель для первого стрелка равна 0,6, для второго - 0,8, для третьего - 0,9. Найти вероятность того, что произойдет не менее двух попаданий.

6.В ремонтной мастерской имеются 4 мотора. Для каждого мотора вероятность того, что он включен, равна 0,9. Найти вероятность того, что в данный момент а) включено 3 мотора; б) включен хотя бы один мотор; в) включено не менее трех моторов.

7.На полке стоят 15 книг, из них пять в переплете. Наудачу берут три книги. Найти вероятность того, что хотя бы одна из взятых книг в переплете.

10