
metodichka_po_pogreshnostyam
.pdfзакономерно, т.е. повторяются от измерения к измерению или изменяются по определенному закону. Так установка на ноль риски микрометра обеспечит одну и ту же ошибку в каждом измерении. А изменение сопротивления проводника из-за его нагревания при пропускании по нему электрического тока приведет к увеличению сопротивления проводника и, следовательно, уменьшению тока в цепи. Значит и показания амперметра будут отличаться от расчетных. Причем, чем больше сопротивление и меньше ток, тем больше это расхождение.
Систематические погрешности связаны с ограниченной точностью изготовления прибора (погрешностью прибора), неправильным выбором метода измерений, неправильной установкой прибора. Они также появляются, если пренебречь действием некоторых внешних факторов.
Погрешности метода измерения – это погрешности, возни-
кающие вследствие несовершенства применяемого метода измерения или из-за наличия допущений и упрощений в применяемых эмпирических формулах. Так, при измерении диаметра шарика измерительной линейкой допускается большая погрешность, чем при использовании штангенциркуля (даже без учета десятых долей миллиметра). Однако, если при помощи штангенциркуля измерять расстояние между двумя точками на бумаге, то на такое измерение уйдет много времени, а точность его будет вряд ли больше, чем при измерении линейкой, хотя сам по себе штангенциркуль способен обеспечить большую точность.
Инструментальные погрешности – это погрешности, воз-
никающие при изготовлении меры или измерительного прибора. Все меры и измерительные приборы делятся на образцовые и
рабочие. Образцовые меры и измерительные приборы служат для воспроизведения и хранения единиц измерения и для проверки и градуировки других мер и измерительных приборов, в частности рабочих, которые используют для практических измерений. Образцовые меры и измерительные приборы дают значения, называемые действительными, рабочие – номинальными.
Погрешностью меры или измерительного прибора называют алгебраическую разность между их номинальным и действительным значениями.
Инструментальную погрешность, взятую с обратным знаком, называют поправкой. Поправки обычно указывают в техническом
10
паспорте прибора. Если средства измерения дают заниженные показания, то поправка, указанная в паспорте, имеет знак «плюс», при завышенных показаниях – «минус».
При обнаружении погрешности от неисправности измерительного прибора следует внести поправку к его показанию. Например, если из-за погнутости стрелки магнитоэлектрического амперметра при отсутствии тока она устанавливается не на нулевой отметке шкалы, а на отметке 0,1 А, т.е. показания завышены, необходимо все показания амперметра уменьшать на 0,1 А; если термометр при измерении температуры тающего снега показывает +1°С, то для такого термометра необходимо брать поправку –1°С.
Погрешности, возникающие в результате неправильной установки и поверки прибора. Измерительные приборы требуют предварительной поверки и определенной установки. Невыполнение этих требований приводит к неверным показаниям. Например, амперметры и вольтметры должны быть установлены в зависимости от указания на приборе (вертикально или горизонтально).
Систематические инструментальные погрешности возникают, если шкала линейки нанесена неточно (неравномерно), положение нуля термометра не соответствует нулевой температуре; капилляр манометра в разных участках имеет разные сечения; при отсутствии электрического тока через амперметр стрелка прибора не устанавливается на нуле и т.д.
Округляя численную величину до какого-либо приближенно-
го значения, например, полагая = 3; = 3,1; = 3,14; = 3,142;= 3,1416 и т.д. вместо = 3,14159265…, мы допускаем систематическую погрешность.
Грубые погрешности (или промахи) обусловлены неисправ-
ностью средств измерений, неправильным отсчитыванием показаний, резкими изменениями условий измерений и т.д. Они приводят к значениям измеряемой величины, резко отличающимся от остальных значений.
При обработке результатов измерений промахи обычно отбрасывают; влияние систематических погрешностей стремятся уменьшить внесением поправок или умножением показаний приборов на поправочные коэффициенты; оценки случайных погрешностей осуществляют методами математической статистики.
11
§2. Закон нормального распределения случайных величин
Получение в серии измерений, проводимых в одинаковых условиях, несколько отличающихся значений одной и той же величины говорит о влиянии случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат измерения многих случайных возмущений и сама является случайной величиной. В этом случае можно лишь с определенной долей уверенности утверждать, что истинное значение случайной величины находится в пределах разброса результатов измерений: от минимального до максимального. Но неясно, какое из множества находящихся в этом промежутке значений принять за результат измерения и какова его случайная погрешность.
Существует подход рассмотрения результатов измерений и случайных погрешностей как случайных величин. Количественные оценки в этом случае позволяют сделать методы теории вероятностей и математической статистики.
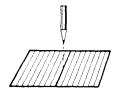
Английский математик Скарборо предложил модель «случайностей» для экспериментального получения распределения случайных погрешностей. Нужно взять лист бумаги, разграфить его на ряд полос шириной 1 см, через середину средней полосы провести цветную линию, которая будет служить прицельной линией. Затем взять карандаш за неоточе-
ный конец двумя пальцами и, прицеливаясь в среднюю линию, отпустить его с высоты одного метра. Карандаш, ударяясь о бумагу, оставит след – точку (рис. 3). Бросая карандаш 50–100 раз, получим совокупность точек, расположенных на различных полосках листа. Полученные результаты можно представить наглядно, построив диаграмму, которая показывала бы, как часто получались при измерениях те или иные значения. Для этого весь диапазон измеренных значений, отложенных по горизонтальной оси, разбивают на равные интервалы, ширина которых x может быть любой и выбирается так, как это удобно. Затем подсчитывают число m значений измеренной величины, попавших в каждый интервал, и на каждом интервале строят прямоугольник с основанием, равным ширине
12

интервала, и высотой, равной числу значений измеренной величи-
ны, попавших в данный интервал (в |
|
|
соответствии с выбранной масштабной |
|
|
единицей). В результате получается |
|
|
диаграмма, изображенная на рис. 4. |
|
|
Такая диаграмма называется гисто- |
|
|
граммой. |
|
|
Если |
количество измерений |
|
|
||
увеличивать |
n , а величину ин- |
Рис. 4. Получение |
тервала уменьшать (интервалы не мо- |
кривой Гаусса. |
|
|
||
гут равняться нулю, но могут быть бесконечно малыми (dx) и приняты за точку), то гистограмма стремится перейти в плавную кривую, линию, приближающуюся к кривой, называемой кривой
плотности распределения вероятностей случайной величины
или кривой Гаусса (рис. 4), а уравнение, описывающее ее, – дифференциальным законом распределения.
Смысл функции плотности распределения вероятностей случайной величины f (x) состоит в том, что f (x)dx показывает
долю значений величины, приходящихся на интервал (x, x dx) (рис. 5). На языке теории вероятностей f (x)dx есть вероятность
того, что результат отдельного измерения окажется в интервале (x, x dx) . Интеграл:
|
x x |
|
P(x) |
f (x)dx |
(1.1) |
x x
дает вероятность того, что отдельное значение х окажется в интер-
вале ( x
x x,
x,  x
x x) . Как
x) . Как
правило указанный интеграл нормируют на единицу, т.е. всю площадь под кривой f (x) принимают равной еди-
нице, тогда площади элементов f (x)dx , являясь долей от
целого, равны вероятности попадания измеряемого зна-
Рис. 5. Функция плотности распределения вероятностей случайной
величины.
чения x в интервал dx . На рис. 5 площадь, равная P(x) , указана
13

редкой штриховкой, f (x)dx – более плотной штриховкой.
В практике измерений встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным (Гауссовым) и равномерным распределением плотности вероятностей. Нормальное распределение случайных погрешностей возникает тогда, когда на результат измерений действует множество случайных возмущений, ни одно из которых не является преобладающим. На практике суммарное воздействие даже небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному.
В аналитической форме нормальный закон распределения случайных величин в 1821 г. предложил немецкий математик Карл Гаусс:
|
|
|
1 |
|
|
( xi x )2 |
|
|
|
f (xi |
) |
|
|
e |
2 2 |
, |
(1.2) |
||
|
|
|
|
|
|||||
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
||
где, xi – случайная величина; <x> – среднее арифметическое; σ – среднее квадратическое отклонение.
Перенеся начало координат в центр распределения <x> и откладывая по оси абсцисс погрешность x = x - <x>, получим кривую нормального распределения погрешностей (рис. 6):
|
|
1 |
|
|
xi |
2 |
|
|
|
f ( x ) |
|
|
e 2 2 |
. |
(1.3) |
||||
|
|
|
|
||||||
i |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для результатов n измерений, распределенных по нормальному закону:
|
|
|
1 |
n |
|
|
|||
|
|
x |
xi |
, |
(1.4) |
||||
|
|
|
|||||||
|
|
|
n i 1 |
|
|
||||
|
|
n |
|
|
|
|
|
|
|
|
|
(xi x )2 |
|
|
|||||
|
i 1 |
|
|
|
|
. |
(1.5) |
||
n 1 |
|||||||||
|
|
|
|
||||||
Можно отметить следующие основные свойства нормального распределения.
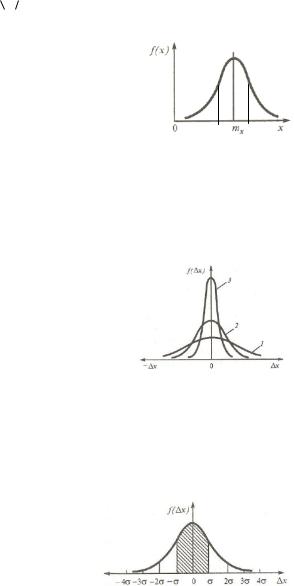
1. Кривая нормального распределения f(Δx) (рис. 6) имеет колоколообразную форму. Характеристиками кривой являются: а)
14
среднее значение  x
x , которое при очень большом числе измерений ( n ) равно истинному значению величины; б) значение
, которое при очень большом числе измерений ( n ) равно истинному значению величины; б) значение
, называемое среним квадратичным |
|
|
|
|
|
|
|
|
|
|
|
отклонением или средней квадратиче- |
|
|
|
|
|
|
f(Δx) |
|
|
||
|
|
|
|
||
ской погрешностью отдельного изме- |
|
|
|
|
|
|
|
|
|
|
|
рения. |
|
|
|
|
|
2. Вершина кривой соответствует |
|
|
|
|
|
наибольшему числу повторений, т.е. |
|
|
|
|
|
|
|
-σ <x> +σ |
x |
||
наиболее вероятному значению. |
|
|
|||
|
|||||
3. Малые погрешности встреча- |
Рис. 6. Кривая нормального |
||||
ются чаще, чем большие. |
распределения. |
|
|||
4. Кривая нормального распре- |
|
|
|
|
|
деления погрешностей относительно вертикальной оси, проходящей через наивысшую точку кривой, симметрична, т.е. одинаковые погрешности, но с различными знаками имеют одинаковую вероятность.
На рис. 7 изображены кривые нормального распределения с различными средними квадратическими отклонениями, причем σ1>σ2>σ3.
Сравнивая кривые между собой можно видеть, что чем меньше среднее квадратичное отклонение, тем меньше рассеяние результатов измерений и тем больше вероятность того, что большинство случайных погреш-
ностей в них будет мало. Естественно заключить, что качество измерений тем выше, чем меньше среднее квадратичное отклонение случайных погрешностей.
Интервал с границами ±Δх называется доверительным ин-
тервалом случайной погреш-
ности, а соответствующая ему вероятность α – доверительной вероятностью. Принято гра-
ницы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения. Доверительные границы слу-
15
чайной погрешности х(α), соответствующие доверительной вероятности α, находят по формуле:
х(α) = t σ, (1.6)
где t – коэффициент, зависящий от α и формы закона распределения.
На графике нормального распределения погрешностей (рис. 8) по оси абсцисс отложены интервалы с границами ±σ, ±2σ, ±3σ, ±4σ. Доверительные вероятности для этих интервалов приведены в
таблице 1. |
|
|
|
|
Как видно из этой таб- |
|
Таблица 1. |
||
лицы, оценка |
случайной по- |
|
||
грешности группы измерений |
Интервал |
Вероятность |
||
=± |
0,6827 |
|||
интервалом ±1σ соответствует |
||||
=±2 |
0,9545 |
|||
доверительной |
вероятности |
|||
=±3 |
0,9973 |
|||
0,68. Такая оценка не дает уве- |
||||
ренности в высоком качестве |
=±4 |
0,999936 |
||
измерений, поскольку 32% от всего числа наблюдений может выйти за пределы указанного ин-
тервала, что совершенно неприемлемо при однократных измерениях и дезинформирует потребителя измерительной информации. Доверительному интервалу ±3σ соответствует α=0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3σ предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи.
Для единообразия в оценке случайных погрешностей при технических измерениях доверительную вероятность α принимают равной 0,95. Лишь для особо точных и ответственных измерений (важных, например, для безопасности и здоровья людей) применяют более высокую доверительную вероятность.
16
ГЛАВА 2. МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
§1. Оценка погрешностей методом статистического учета
1.1. Расчет абсолютной и относительной погрешностей прямых измерений
Измерения одной и той же величины дают в общем случае результаты, несколько отличающиеся друг от друга даже тогда, когда они производились одним и тем же лицом, одним и тем же способом, посредством одних и тех же приборов. Допустим, что мы произвели n прямых (непосредственных) измерений некоторой физической величины, истинное значение которой (нам неизвестное) обозначим через x. Обозначим через x1, x2, x3, …, xn результаты отдельных измерений, а через xi = x - xi – абсолютную погрешность n-го измерения. Абсолютной погрешностью измеряемой величины называется разница между истинным и измеренным значениями этой величины. Абсолютная погрешность измеряется в единицах измеряемой величины. Тогда результаты измерений можно представить в виде:
xi = x - xi, где i=1, 2, 3, … , n (2.1)
Естественно, что абсолютные погрешности xi могут принимать как положительные, так и отрицательные значения. Суммируя левую и почленно правую стороны равенств (2.1), имеем:
n
xi
i 1
n |
|
nx xi . |
(2.2) |
i 1
Разделив обе стороны равенства (2.2) на число измерений п, получим после перестановки членов:
|
|
|
1 |
n |
|
|
|
|
x x |
xi , |
(2.3) |
||
|
|
|
||||
|
|
|
n i 1 |
|
||
|
1 |
n |
|
|
|
|
где x |
xi –среднеарифметическая величина. |
(2.4) |
||||
|
||||||
|
n i 1 |
|
|
|
||
Если число измерений п достаточно велико (строго говоря, при n ), получим равенство:
17
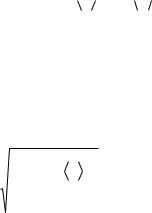
|
1 |
n |
|
|
|
lim |
xi |
0 , |
(2.5) |
||
|
|||||
n n i 1 |
|
|
|||
так как в серии из большого числа измерений всякой положительной погрешности можно сопоставить равную ей по абсолютной величине отрицательную погрешность. Из (2.3) и (2.5) следует:
при n , x x , |
(2.6) |
т.е. при бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению.
Однако при ограниченном числе измерений n среднеарифметическое значение будет отличаться от истинного значения, т.е. равенство (2.6) будет не точным, а приближенным: x x .
Нам необходимо оценить величину этого расхождения. Появление того или иного значения xi, в процессе измерения
является случайным событием. Существует некоторая вероятность появления этого значения в интервале (  x
x x,
x,  x
x x ), а сле-
x ), а сле-
довательно, и появления соответствующего значения абсолютной погрешности xi.
Задавая вероятность того, что истинное значение измеряемой величины x попадает в данный доверительный интервал, другими словами, задавая надежность α по числу проведенных измерений n можно определить значение коэффициента Стьюдента t ,n (см. приложение 7) и, следовательно, найти случайную абсолютную погрешность xслуч:
|
|
n |
|
|
|
|
|
(xi |
x )2 |
|
|
xслуч |
t ,n |
i 1 |
|
. |
(2.7) |
|
|
||||
|
|
n(n 1) |
|
||
Эта погрешность является только частью совершаемой ошибки, обусловленной случайными причинами. Полная же абсолютная погрешность складывается из случайной погрешности и погрешности измерительного прибора. Последняя при выполнении лабораторных работ физического практикума, если неизвестен класс точности прибора, может быть определена как наименьшая цена деления измерительного прибора :
xпр . |
(2.8) |
Тогда полная абсолютная погрешность измеряемой величины мо-
18

жет быть рассчитана так:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
( xi x |
)2 |
|
|
x |
|
|
( x |
|
)2 ( x |
|
)2 |
|
t |
i 1 |
|
|
2 . (2.9) |
||
полн |
случ |
пр |
|
|
|
||||||||||
|
|
|
|
|
|
|
,n |
n(n 1) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее под x будем понимать полную абсолютную погрешность измеряемой величины.
После того, как полная абсолютная погрешность посчитана, результат измерений можно записать в виде: x  x
x x . Это оз-
x . Это оз-
начает, что истинное значение величины x с надежностью α попадает в этот доверительный интервал.
Следует отметить, что величина абсолютной погрешности x результата измерений сама по себе еще не определяет точности измерений.
Пусть, например, измеряя длину карандаша рулеткой, разделенной на сантиметры, мы получили, что эта длина равна l=18,0±0,5 см (±0,5 см составляет погрешность ленты рулетки). Если при помощи этой же рулетки мы измерим диаметр карандаша, то получим d=0,5±0,5 см. Хотя абсолютная погрешность измерений одинакова, точность измерений различна. Если в первом случае измерения достаточно точны, то во втором случае значение погрешности сравнимо по порядку с измеряемой величиной, что позволяют судить лишь о порядке величины.
Для оценки точности измерений вводится понятие относительной погрешности ε, равной отношению абсолютной погрешности x результата измерений к среднему значению:
|
x |
. |
(2.10) |
|
|||
|
x |
|
|
В таком виде эта погрешность выражается в долях от единицы. Если же умножить ее на 100%, то она будет представлена в процентах:
|
x |
100% . |
(2.11) |
|
x |
||||
|
|
|
За меру точности измерения принимают величину, обратную ε. Следовательно, чем меньше относительная погрешность ,
19
