Методы аналитических вычислений

> f := x -> x^2;

Первая строка определяет f как сокращенное обозначение выражения x2; вторая строка определяет f как функцию от x. После определения f таким образом, f(x) действует так, как и надлежит:

> f(3), f(10), f(x), f(y), f(a + b);

Предупреждение: Команда f(x) := x^2 делает четыре символа слева сокращенным обозначением для трех символов справа; такая команда не определяет функцию!

Авот пример векторно-значной функции двух переменных:

>h := (x,y) -> linalg[vector] ([x^2-y^2,2*x*y]): h(u,v);

[u2 – v2, 2 u v]

Функции часто оказываются более полезными, чем выражения. Однако, многие команды Maple (например, diff) предполагают, что на их входе будет выражение.

Если ввести

> f:= x -> x^2, diff(f,x);

то такая команда не сработает; однако,

> diff(f(x),x);

будет работать, поскольку результатом f(x) является x2; работает также

> diff(f(y),y);

выдавая 2y . [Между прочим, имеется вариант дифференцирования для "функции"; введите

?D для получения дополнительной информации].

Когда функция "прилагается" ("applied") к переменной, то в результате получается выражение. Чтобы превратить выражение в функцию, воспользуйтесь командой unapply:

> f := unapply(x^3, x); f(3);

Эта команда часто используется в связи с solve, например:

> soln := solve( y = x^2 - a, x);

Имеются два решения, к которым можно обратиться как к soln[1] и soln[2] (обратите внимание на квадратные скобки). Предположим, что вы хотите использовать второе из этих выражений, чтобы определить функцию; это делается следующим образом:

21

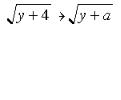
>g := unapply(soln[2], a);

>g(x); g(4);

УПРАЖНЕНИЯ:

*Поэкспериментируйте со "стрелочным обозначением" для создания функций.

*Поэкспериментируйте с выражениями и командой unapply для создания функций.

Процедуры

Функции являются частным случаем процедур. Процедура - это совокупность команд, подобная "подпрограмме" в некоторых компьютерных языках.

Функция, определенная выше как f := x -> x^2; это то же, что и

> f := proc(x) x^2 end;

Процедуры полезны для более сложных работ, которые могут охватывать много строк, учитывать выбор из многих различных случаев, или выполнять много действий. Рассмотрим еще один короткий пример процедуры:

> sqroot := proc(x)

#Вычисляет квадратный корень по методу Ньютона local xstart, xnew, i;

xstart := 1.;

for i from 1 to 100 do

xnew := ( xstart + x/xstart )/2;

print(xnew);

if abs(xnew - xstart)/xnew < 10^(-4) then RETURN() fi; xstart := xnew;

od;

end:

Заметим, что для получения нескольких строк после одного приглашения к вводу ">" следует воспользоваться Shift+Enter.

22

После создания этой процедуры, она дает:

> sqroot(2);

1.500000000

1.416666667

1.414215687

1.414213563

УПРАЖНЕНИЯ:

*Напишите процедуру bigger, такую, чтобы команда bigger(n,m); печатала true если n больше чем m, и false, если n меньше чем m.

*Напишите процедуру squaresum, вычисляющую сумму квадратов первых 100 натураль-

ных чисел (т.е., 1+4+9+...+10000).

*Сравните вашу squaresum(100) с sum(n^2, n=1 .. 100).

*Видоизмените вашу процедуру squaresum так, чтобы вычислять сумму первых N квадратов, где N это любое натуральное число.

8. ПОИСК И УСТРАНЕНИЕ ОШИБОК

Хотя на первых порах ошибки в работе с Maple могут очень вас смущать, вы быстро приобретете опыт, необходимый для того, чтобы понимать и исправлять их. Приведем список наиболее распространенных ошибок и способов их устранения.

1.Оканчивается ли оператор точкой с запятой или двоеточием?

2.Сбалансированы ли круглые скобки, фигурные скобки, квадратные скобки и т.д.? Набор символов наподобие {x, y} хорош, но x, y} может привести к ошибке.

3.Не пытаетесь ли вы использовать что-либо в качестве переменной, которой вы уже присвоили значение? Чтобы "очистить" переменную x, скажите unassign('x') или x:='x'. Вы можете очистить сразу несколько переменных, например, unassign('x', 'y'). Вам не придется перезагружать какие-либо пакеты. Помните, что переменная, которой присвоено значение, не может более работать как переменная. Чтобы отобразить значение простой переменной, введите ее имя с последующей точкой с запятой, например, > x;

4.Если дело кажется безнадежно запутанным, дайте команду > restart; После этого вам придется перезагрузить все необходимые пакеты.

5.Не используете ли вы функцию, когда было вызвано выражение, или наоборот? Помните, ff:=x^2+y^2 определяет выражение, тогда как f:=(x,y)->x^2+y^2 определяет функцию. Имеет смысл сказать f(1,3), но нет никакого смысла говорить ff(1,3).

23

6.Не используете ли вы = когда требуется := ? Помните, что первое это проверка на равенство, в то время как второе присваивает значение переменной.

7.Различаете ли вы три вида кавычек? Это: " (двойная кавычка), ' (одинарная кавычка – апостроф), и ` (обратная кавычка).

8.В операторах цикла, do должно быть сбалансировано последующим od. В условных операторах, if должно быть сбалансировано последующим fi.

последующим end. После proc(…) точка с запятой не ставится!

10.Если вы используете функцию из пакета, загрузите сначала пакет. Так, чтобы использовать matrix, загрузите linalg; чтобы использовать display, загрузите plots. Вы загрузите linalg командой with(linalg).

11.Не путайте unassign с unapply.

12.Не забывайте использовать ? для получения подробной справки о функции Maple, например, ?plot для получения информации о plot, или просто ? для получения общей информации.

9. ЗАДАНИЯ И УПРАЖНЕНИЯ

3.Вычислите первую и вторую производные от sin x cos x по x.

4.Дан многочлен: y(x) = x3 - 4x2 + 4x - 1 . Найдите корни этого многочлена и все его локальные минимумы и максимумы. Проконтролируйте это решение, построив график функции y(x).

5.Дано f = x2 - 4. Вычислите интегралы от f и 1/f по x. Проверьте правильность результа-

тов путем их дифференцирования.

8. Получите формулу для суммы первых n натуральных чисел, а также для суммы квадра-

24

ристического многочлена.

11. Воспользуйтесь командой solve для решения линейной системы:

4x −5y =11,

2x + y = 9.

12. Найдите разложение функции sin(x) в ряд Тейлора до членов порядка 6 в точке x = 0, используя команду taylor. Затем с помощью команды convert преобразуйте полученное выражение в многочлен (без остаточного члена). Для наглядного представления о точности такой аппроксимации постройте одновременно графики sin(x) и полученного многочлена 6-

й степени при x [0,4].

12a. Повторите такие же операции для разложения sin(x) в ряд Тейлора до членов порядка 10.

13.Решите задачи NN 12, 12a, но с использованием команды series (и стандартной переменной Order, определяющей порядок разложения.

14.Используйте команду limit, чтобы найти пределы функции:

Теперь рассмотрим задания, связанные с дифференциальными уравнениями. Для решения дифференциальных уравнений можно, в частности, использовать команду дифференцирования diff и команду – "решатель ОДУ" dsolve.

25

15. Решите систему ОДУ:

x'(t) = −x(t) + ay(t ), y'(t ) = bx(t ) − y(t ).

при начальных условиях x(0) = 1, y'(0) = 0. 16. Решите ОДУ 2-го порядка:

a)y(x) + y"(x) = ex

при начальных условиях y(0) = 1, y'(0) = 0.

б) y"(t) + 5 y'(t) + 6 y(t) = 0

при начальных условиях y(0) = 0, y'(0) = 1.

Примечание: Команда дифференцирования для функции имеет вид D, для выражений эта команда имеет вид diff.

17. Решите ОДУ 4-го порядка: 106 yIV(x) = δ(x-2) - δ(x-4)

при граничных условиях на y(x) и y"(x):

Дельта-функция Дирака δ(x) в Maple записывается как Dirac(x).

Решение этой краевой задачи сохраните под именем "soln", а затем постройте график найденной функции для x = 0..5.

18.Решите систему двух ДУ 2-го порядка: y"(x) = z(x),

z"(x) = y(x),

не вводя дополнительных условий. Maple создаст соответствующие константы C1,...,C4.

Общие указания к NN 15-18:

1.Проверьте правильность найденных вами решений дифференциальных уравнений путем их подстановки в уравнения.

2.Попробуйте поработать с пакетом "DEtools"

26

ПРИЛОЖЕНИЕ 1.

Maple V Release 5: КРАТКАЯ СПРАВКА

Символы и сокращения

27

Команды

28

ПРИЛОЖЕНИЕ 2.

ПОСТРОЕНИЕ СПЛАЙН-ПОВЕРХНОСТИ СРЕДСТВАМИ Maple V

В качестве примера, иллюстрирующего возможность использования системы Maple V при решении сложных содержательных проблем, рассмотрим задачу построения и визуализации сплайн-поверхности, восстанавливающей функцию двух переменных по ее значениям в конечном числе произвольных точек плоскости (см., например: Сплайн-поверхности: Методическая разработка. Сост. В.О. Ашкеназы. - Тверь: Тверской гос. ун-т, 1993).

Если функция двух переменных f (x, y) задана своими значениями в конечном числе то-

чек:

{(xi , yi ), fi = f (xi , yi ); i =1, N },

то ее можно интерполировать сплайн-поверхностью Sp (x, y) , которая является решением вариационной задачи

Это решение имеет достаточно простой вид:

29

Решение существует и является единственным, если N ≥ 3 и среди N точек (xi , yi ) най-

максимальная абсолютная погрешность.

А теперь запишем соответствующую программу на языке Maple V Release 5.

Построение сплайн-поверхности*

Начнем с того, что зададим некоторую тестовую функцию:

>restart;

>f: = (x,y) -> x^2 + y^2;

Вызовем необходимые для дальнейшей работы пакеты linalg и plots :

> with (linalg): with (plots):

Warning, new definition for norm Warning, new definition for trace

Опишем процедуру ввода случайной последовательности N точек в квадрате −1 < x, y ≤1 :

> Vv := proc (N) local p,pt,i; p := rand (-100..100);

pt := [seq (p(i)/100., i = 1..2*N)]; matrix (N, 2, pt);

end:

Теперь зададим N=10 и получим соответствующий двумерный массив T, содержащий координаты десяти узлов интерполяции:

>N := 10:

>T := Vv(N):

Сформируем матрицу MM системы линейных алгебраических уравнений для вычисления коэффициентов сплайн-поверхности:

> Ro := proc (x1,x2,y1,y2) local r; r := (x1-x2)^2 + (y1-y2)^2;

if r = 0 then 0 else r*ln(r) fi end:

>M := matrix (N, N, []):

>i := 1:

>while i <= N do M [i, i] := 0;

* Первоначальный вариант этой Maple-программы был разработан Соколовой Н.А. в 1998 г.

30