Лекция 4_Системы счисления

Лабораторная работа 1. «Системы счисления»

Система счисления – это правила записи чисел с помощью заданного набора специальных знаков – цифр.

Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп: унарная, непозиционные и позиционные.

Две первые представляют скорее исторический интерес, поскольку имеют весьма ограниченное применение в настоящее время.

Унарная система счисления

Унарная система счисления – это система счисления, в которой для записи чисел используется только один знак – 1 («палочка»).

Следующее число получается из предыдущего добавлением новой 1; их количество (сумма) равно самому числу.

Именно такая система применяется для начального обучения счету детей (можно вспомнить «счетные палочки»).

Другими словами, использование именно унарной системы оказывается важным педагогическим приемом для введения детей в мир чисел и действий с ними.

Непозиционные система счисления

Непозиционная система счисления - система, в которой символы, обозначающие то или иное количество, не меняют сво­его значения в зависимости от местоположения (позиции) в изоб­ражении числа.

Из непозиционных наиболее распространенной можно считать римскую систему счисления.

В ней некоторые базовые числа обозначены заглавными латинскими буквами:

1 – I, 5 – V, 10 – X, 50 – L , 100 – C, 500 – D, 1000 – M.

Все другие числа строятся из комбинаций базовых, причем:

1. если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой;

2. если цифра справа меньше или равна цифре слева, то эти цифры складываются;

Запись чисел в такой системе громоздка и неудобна, но еще более неудобным оказывается выполнение в ней даже самых простых арифметических операций.

Наконец, отсутствие нуля и знаков для чисел больше M не позволяют римскими цифрами записать любое число (хотя бы натуральное). Используется эта система для нумерации.

Позиционные системы счисления

Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

Упорядоченный набор символов (цифр) {а₀, a_v ..., а_п), используемый для представления любых чисел в заданной позиционной си­стеме счисления, называют ее алфавитом, число символов (цифр) алфавита р = п + 1 - ее основанием, а саму систему счисления называют р-ричной.

Основание позиционной системы счисления - количество различных цифр, используемых для изображения чисел в данной системе счисления.

Самой привычной для нас является десятичная система счисле­ния. Ее алфавит - {0, 1, 2, 3, 4, 5, б, 7, 8, 9}, а основание р = 10, т. е. в этой системе для записи любых чисел используется только десять разных символов (цифр). Десятичная система счисления основана на том, что 10 единиц каж­дого разряда объединяются в одну единицу соседнего старшего разряда, поэтому каждый разряд имеет вес, равный степени 10. Сле­довательно, значение одной и той же цифры определяется ее местоположением в изображении числа, характеризуемым степенью числа 10. Например, в изображении числа 222.22 цифра 2 повторяется 5 раз, при этом первая слева цифра 2 означает количество сотен (ее вес равен 10²); вторая - количество десятков (ее вес равен 10¹), третья - количество единиц (ее вес равен 10⁰), четвертая - количество десятых долей единицы (ее вес равен 10^-1) и пятая цифра - количество сотых долей единицы (ее вес равен 10 ^-2), т. е. число 222.22 может быть разложено по степеням числа 10:

222.22 = 2 • 10² + 2 •10¹ + 2 • 10° + 2 • 10^-1 + 2 • 10^-2.

Аналогично 725 = 7 • 10² + 2 • 10¹ + 5 • 10°;

1304.5 = 1 • 10³ + 3•10² + 0 • 10¹ + 4 • 10° + 5 • 10^-1,

50328.15 = 5 • 10⁴ + 0 • 10³ + 3 • 10² + 2 • 10¹ + 8 • 10° + 1 • 10 ^-1 + 5 • 10^-2.

В общем случае для задания р-ричной системы счисления необходимо определить основание р и алфавит, состоящий из р различ­ных символов (цифр) а_р i = 1,..., р.

Любое число X_p можно представить в виде поли­нома путем разложения его по степеням числа p:

(1)

последовательность из коэффициентов которого представляет со­бой сокращенную запись числа X_p :

(2)

Точка, отделяющая целую часть числа от дробной, служит для фиксации конкретных значений каждой позиции в этой последо­вательности цифр и является началом отсчета.

Методы перевода чисел. Представление чисел в различных системах счисления

Перевод чисел из одной системы счисления в другую

Одно и то же число может быть записано в различных системах счисления.

Алгоритм перевода целых чисел из q-ричной системы в p-ричную, при q > p

Для замены исходного числа X_q равным ему числом X_p нужно по правилам q-ричной арифметики целочисленно делить X_q на новое основание p. Результаты деления, записанные в порядке от последнего к первому, и окажутся цифрами X_p.

Пример:

Поскольку коэффициенты многочлена неизвестны, обозначим их a_i; получаем:

123₁₀ = 443₅

Обычно описанную процедуру представляют в виде привычной по школе операции деления:

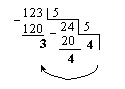
Таким образом, получили X₅=443.

Проверяем правильность перевода: 4*5²+4*5¹+3*5⁰=100+20+3=123₁₀.

Полученное число нельзя читать «четыреста сорок три». Прочитывать число следует простым перечислением его цифр с указанием системы счисления («число четыре, четыре, три в пятиричной системе счисления»).

Второе, на что нужно обратить внимание – все операции выполнялись по правилам арифметики той системы счисления, от которой осуществлялся перевод (в рассмотренном примере – десятичной).

Алгоритм перевода целых чисел из q-ричной системы в p-ричную, при q < p

Для перевода необходимо представить число X_q в форме многочлена и выполнить все операции по правилам p-ричной арифметики.

Пример:

X₆  X₁₀, Х= 234₆

234₆ = 26²+36¹+46⁰ = 236+36+41 = 94₁₀

Приведенными алгоритмами удобно пользоваться при переводе числа из десятичной системы в какую-то иную или наоборот.

Они работают и для перевода между любыми иными системами счисления, однако, такой перевод будет затруднен тем, что все арифметические операции необходимо осуществлять по правилам исходной (в первом алгоритме) или конечной (во втором алгоритме) системы.

По этой причине переход, например X₃  X₈ проще осуществить через промежуточный переход к 10-ной системе X₃  X₁₀  X₈.

Алгоритм перевода правильной дроби при q > p

Результатом перевода правильной дроби 0,X_q будет также правильная дробь 0,X_p, которая получится в результате умножения исходной дроби на новое основание p по правилам q-ричной арифметики; целая часть полученного произведения будет цифрой старшего разряда новой дроби; дробную часть полученного произведение следует снова умножить на p и т.д.

Пример: 0,X₁₀  0,X₂. 0,Х=0,375₁₀

Тогда для получения 0,X_2:

0,375*2 = 0,750

0,75*2 = 1,50

0,5*2 = 1,0

Таким образом, 0,375₁₀ = 0,011₂.

Проверяем 0,011=0*2^-1+1*2^-2+1*2^-3=0,25+1,125=0,375₁₀

Алгоритм перевода правильной дроби при q < p

Для перевода X_q  X_p необходимо представить число X_q в форме многочлена и выполнить все операции по правилам p-ричной арифметики.

Пример: X₆  X₁₀, Х₆=0,234₆

Для этого

0,234₆ = 26^-1+36^-2+46^-3=0,33(3)+0,083(3)+0,01(851)= 0,43517₁₀

Проверяем:

0, 43517*6=2,61102

0, 61102*6=3,66612

0,66612*6=3,996724,0 {погрешность вычислений в случае получения иррациональных чисел}

Пример: X₂  X₁₀, Х=0,10101₂

Для этого

0, 10101₂ = 12^-1+02^-2+12^-3 +02^-4+12^-5= 0,5+0,125+0,03125= 0,65625_10.

Проверяем:

0,65625*2=1,3125

0,3125*2=0,625

0,625*2=1,25

0,25*2=0,5

0,5*2=1,0_. Все верно

Перевод чисел между системами счисления 2 – 8 – 16

Примеры изображения чисел в данных системах счисления приведены в таблице 1

Таблица 1. Системы счисления

десятичная	двоичная	8-ричная	16-ричная	десятичная	двоичная	8-ричная	16-ричная
0	00000	0	0	11	01011	13	В
1	00001	1	1	12	01100	14	С
2	00010	2	2	13	01101	15	D
3	00011	3	3	14	01110	16	Е
4	00100	4	4	15	01111	17	F
5	00101	5	5	16	10000	20	10
6	00110	6	6	17	10001	21	11
7	00111	7	7	18	10010	22	12
8	01000	10	8	19	10011	23	13
9	01001	11	9	20	10100	24	14
10	01010	12	А

Для перевода целого двоичного числа в систему счисления с основанием p = 2^r достаточно данное двоичное число, начиная с младшего разряда, разбить на группы в r цифр каждая и каждую группу независимо перевести в систему p.

Например, для перевода числа 110001₂ в систему счисления p=8, нужно разбить исходное число на группы по три разряда справа налево (8 = 2³, следовательно, r = 3) и перевести в 8-ричную систему счисления: 110001₂=61₈. Проверяем 110001₂=32+16+1=49₁₀, 6*8¹+1*8⁰=49₁₀

Аналогично, разбивая на группы по 4 двоичные цифры, получим 110001₂ = 31₁₆.

Для перевода целого числа, записанного в системе счисления с основанием p = 2^r, в двоичную систему достаточно каждую цифру исходного числа независимо заменить соответствующим r-разрядным двоичным числом, дополняя его при необходимости незначащими нулями до группы в r цифр.

Пример: представим число D3₁₆ в двоичной системе счисления:

Пример, 123₈ = 001010011₂ = 53₁₆.

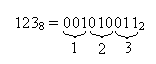
Задания для самостоятельного выполнения

1. Переведите число X_p p-ричной системы счисления в X_q q-ричной системы счисления

1. X₅  X₁₀, где X₅=123

2. X₃  X₁₀, где X₃=102

3. X₁₀  X₄, где X₁₀=123

4. X₁₀  X₆, где X₁₀=548

5. X₅  X₃, где X₃=421

6. X₂  X₆, где X₂=0111001

7. X₂  X₁₆, где X₂=10011

8. X₂  X₈, где X₂=101010

9. X₁₆  X₂, где X₁₆=AD3

10. X₈  X₂, где X₈=5470

II. Переведите десятичное число в двоичное:

1. 743₁₀, b) 334.12₁₀, c) 61.375, d) 160.25₁₀, e) 131.82₁₀

III. Переведите десятичное число в шестнадцатеричное число:

1. 445₁₀, b) 334.12₁₀, c) 261.375, d) 160.25₁₀, e) 131.82₁₀