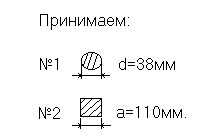2.2. Условие прочности

Для решения вопроса о прочности, в соответствии с принятым методом расчёта на прочность по допускаемым на­пряжениям и условием прочности (1.4), запишем это условие применительно к растянутому (сжатому) стержню.

, (2.3)

где |N_max| – максимальная по абсолютному значению продольная сила;

F – пло­щадь поперечного сечения стержня;

[σ] – допускаемое напряжение.

При реше­нии задач сопротивления материалов [σ] всегда задано. При расчётах машин или конструкций Нормы расчёта дают указания по поводу назначения или расчёта [σ]. Формула (2.3) применима для стержня из материала, имею­щего одинаковую прочность на растяжение и на сжатие (например, для стали). Но если материал по-разному сопротивляется растяжению и сжатию (напри­мер, чугун) для расчёта на прочность необходимо учитывать знак продольной силы и записывать два условия прочности

,, (2.4)

где N_max – наибольшая (растягивающая) продольная сила;

N_min – наименьшая (сжимающая) продольная сила;

[σ₊] и [σ_-] – допускаемые напряжения на растяжение и на сжатие соответственно.

Значение N, входящее в условие прочности, определяется предварительно по эпюреN(рис.2.3.) или из расчёта статического равновесия конструкции.

Рассмотрим пример. Необходимо определить размеры поперечного сечения стержней кронштейна, удерживающего нагрузку P= 100 кН (рис.2.6).

Стержень №1: стальной, круглый, [σ] = 160 МПа; стержень №2: деревянный, квадратный, [σ] = 12 МПа.

Рис.2.6

Сначала найдём усилия в стержнях. Для такой системы можно записать два уравнения статики:

∑ х = 0: – N₂ – N₁cos α = 0,

∑ y = 0: – P + N₁sin α = 0.

.

Из уравнения ∑ y = 0 найдём .

Из уравнения ∑ х = 0 найдём N₂ = – N₁cos α = – 166,7 ∙ 0,8 = – 133,3 кН.

Из условия прочности найдём площади поперечного сечения стержней

, .

При расчётах прочности величину допускаемого напряжения, заданную в МПа, перевели в кН/см²: 160 МПа = 16 кН/см² и 12 МПа = 1,2 кН/см². Теперь осталось определить размеры поперечных сечений.

2.3. Деформации. Закон Гука

Рассмотрим деформации, возникающие при растяжении и сжатии стержней. При растяжении длина стержня увеличивается, а поперечные размеры сокра­щаются. При сжатии, наоборот, длина стержня уменьшается, а поперечные размеры увеличиваются. На рис.2.7 пунктиром показан деформированный вид растянутого стержня.

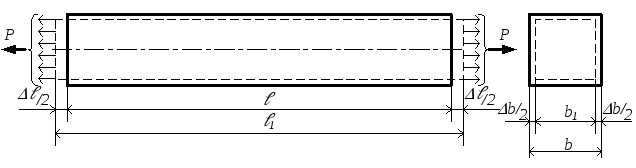
Рис.2.7

ℓ – длина стержня до приложения нагрузки;

ℓ₁ – длина стержня после приложения нагрузки;

b – поперечный размер до приложения нагрузки;

b₁ – поперечный размер после приложения нагрузки.

Абсолютная продольная деформация ∆ℓ = ℓ₁ – ℓ.

Абсолютная поперечная деформация ∆b = b₁ – b.

Значение относительной линейной деформации ε можно определить как отношение абсолютного удлинения ∆ℓ к первоначальной длине бруса ℓ

. (2.5)

Аналогично находятся поперечные деформации

. (2.6)

При растяжении поперечные размеры уменьшаются: ε > 0, ε′ < 0; при сжатии: ε < 0, ε′ > 0. Опыт показывает, что при упругих деформациях поперечная всегда прямо пропорциональна продольной.

ε′ = – νε. (2.7)

Коэффициент пропорциональности ν называется коэффициентом Пуассона или коэффициентом поперечной деформации. Он представляет собой абсолютную величину отношения поперечной деформации к продольной при осевом растяжении

. (2.8)

Назван по имени французского учёного, впервые предложившего его в начале XIX века. Коэффициент Пуассона есть величина постоянная для материала в пределах упругих деформаций (т.е. деформаций, исчезающих после снятия нагрузки). Для различных материалов коэффициент Пуассона изменяется в пределах 0 ≤ ν ≤ 0,5: для стали ν = 0,28…0,32; для резины ν = 0,5; для пробки ν = 0.

Между напряжениями и упругими деформациями существует зависимость, известная под названием закон Гука:

σ = Еε. (2.9)

Коэффициент пропорциональности Е между напряжением и деформацией называется модулем нормальной упругости или модулем Юнга. Размерность Е такая же, как и у напряжения. Так же, как и ν, Е – упругая постоянная материала. Чем больше значение Е, тем меньше, при прочих равных условиях, продольная деформация. Для стали Е = (2...2,2)10⁵ МПа или Е = (2...2,2)10⁴ кН/см².

Подставляя в формулу (2.9) значение σ по формуле (2.2) и ε по формуле (2.5) , получим выражение для абсолютной деформации

. (2.10)

Произведение EF называется жёсткостью бруса при растяжении и сжатии.

Формулы (2.9) и (2.10) – это разные формы записи закона Гука, предложенного в середине XVII века. Современная форма записи этого фундаментального закона физики появилась гораздо позже – в начале XIX века.

Формула (2.10) справедлива лишь в пределах тех участков, где сила N и жёсткость EF постоянны. Для ступенчатого стержня и стержня, нагруженного несколькими силами, удлинения подсчитываются по участкам с постоянными N и F и результаты суммируются алгебраически

. (2.11)

Если эти величины изменяются по непрерывному закону, ∆ℓ вычисляется по формуле

. (2.12)

В ряде случаев для обеспечения нормальной работы машин и сооружений размеры их деталей должны быть выбраны так, чтобы кроме условия прочности обеспечивалось условие жёсткости

, (2.13)

где ∆ℓ – изменение размеров детали;

[∆ℓ] – допускаемая величина этого изменения.

Подчёркиваем, что расчет на жёсткость всегда дополняет расчёт на прочность.