Фигурами

 

 

1. Совпадают  (АВ)  (CD) – прямая АВ, проходящая через точки А и В, совпадают с прямой CD, проходящей через точки C и D.

2. Конгруэнтны   АВС   MNK – угол АВС конгруэнтен углу MNK.

3. Параллельны     – плоскость  параллельна плоскости .

4. Перпендикулярны  a  b – прямые a и b перпендикулярны.

5. Скрещиваются  c  d – прямые c и d скрещиваются.

6. Отображаются  Ф₁  Ф₂ – фигура Ф₁ отображается на фигуру Ф₂.

7. Центр проецирования – S.

8. Направление проецирования – s.

9. Принадлежность – , , точка Аa – принадлежит прямой a; A  a – прямая a проходит через точку А.

10 .Включение (содержит в себе) –  ,  , a   – прямая a принадлежит плоскости .

11.Объединение –  , ABCD = |AB|  |BC|  |CD| ломаная линия, ABCD.

12. Пересечение множеств  , – a  b – прямые a и b пересекаются, a =    – прямая есть пересечение плоскостей  и .

13. Конъюнкция предложений – , соответствует союзу «и».

14. Дизъюнкция предложений – , соответствует союзу «или».

15. Импликация  – это логическое следствие.

16. Эквивалентность: справедливо как утверждение – ,    так и ему обратное   .

17. Квантор общности, , читается: для всякого, для всех, для любого. Выражение (x) P(x) означает: для всякого x имеет место свойство P(x).

18. Квантор существования, читается: существует – ,  xX существует элемент x множества X такой, что …

19. Квантор единственного существования -₁.

 

 

20. Латинский алфавит 21. Греческий алфавит

A, a – a A,  – альфа

B, b – бэ B,  – бэта

C, c – цэ Г,  – гамма

D,d – дэ ,  – дельта

E, e – e E,  – эпсилон

F, f – эф Z,  – дзета

G, g – же H,  – эта

H, h – ха (аш) ,  – тэта

I, i – и I, i – йота

J, j – йот (жи) K,  – каппа

K, k – ка ,  – лямбда

L, l – эль M,  – мю

M, m – эм N,  – ню

N, n – эн ,  – кси

O, o – о O, o – омикрон

P, p – пэ П,  – пи

Q,q – ку Р,  – ро

R, r – эр ,  – сигма

S, s – эс Т,  – тау

T, t – тэ , – ипсилон

U, u – у Ф,  – фи

V,  – вэ Х,  – хи

W,  – дубль–вэ ,  – пси

X, x – икс ,  – омега

Y, y – игрек

Z, z – зет

 

Указанные обозначения используются при решении позиционных и метрических задач в курсе инженерной и машинной графики.

1 Метод проекций

 

 

В процессе проектирования, при расчете и разработке конструкций, возникают пространственные задачи. Многие из этих задач решаются графическими методами, при котором геометрические свойства фигур изучаются непосредственно по чертежу.

Чертежом, геометрически равноценным изображаемой фигуре или оригиналу, является проекционный чертеж, полученный методом проецирования.

Начертательная геометрия основана на методе проекций. Поэтому проекционный метод изображений является основным методом начертательной геометрии.

Способ центрального проецирования, параллельного проецирования и, как частный случай его, способ ортогонального проецирования предполагает проецирующий аппарат, включающий в себя плоскость проекций ', объект проецирования и центр проецирования S.

Пусть будут даны: плоскость ', точка S (S ') и некоторая точка А

(А  S)  (А  S).

На рисунке 1 центральной проекцией

точки А является точка А' пересечения пря-

мой SA с плоскостью '. Плоскость ' назы-

вают плоскостью проекций, точку S – центром проецирования, луч [SA') - проецирующим лучом.

Положения плоскости ' и центра S

определяет аппарат проецирования. При за-

данных плоскости проекций и центра проек-

ций можно построить проекцию точки; но

имея проекцию (А'), нельзя по ней определить положение самой точки А в пространстве,

Рисунок 1

так как любая точка проецирующей прямой линии SA проецируется в одну и ту же точку. Для однозначного определения точки А в пространстве по ее проекции необходимо задать второй центр проецирования, т.е. для определения положения точки в пространстве необходимо иметь две ее центральные проекции, полученные из двух различных центров (рисунок 2).

Таким образом, если центр проекций S задан в конечной точке, не лежащей в плоскости проекций ', то проецирование является центральным.

 

 

 

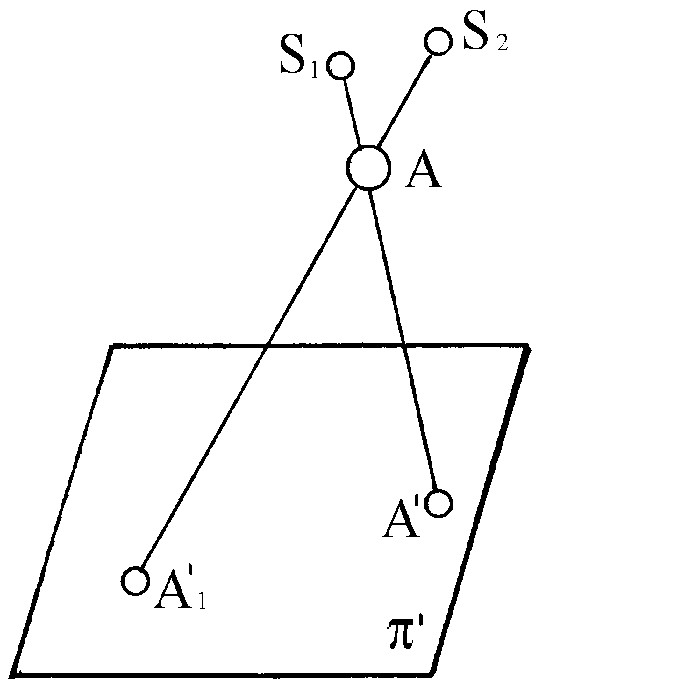
Рисунок 2

 

Центральные проекции применяют для построения предметов в перспективе, например, в архитектурно-строительных чертежах, при изображении перспектив зданий, улиц, площадей и т. п. Изображения в центральных проекциях наглядны, но для технического черчения неудобны.

Параллельное проецирование является частным случаем центрального проецирования, когда центр проецирования S бесконечно удален от плоскости проекций '. В этом случае проецирующие прямые будут параллельны между собой, проведенные в заданном направлении относительно плоскости проекций (рисунок 3).

Рисунок 3

Параллельные проекции делятся на косоугольные и прямоугольные. В

первом случае направление проецирования составляет с плоскостью проекций

угол, не равный 90^о, во втором случае проецирующие прямые перпендикулярны к плоскостям проекций.

Наибольшее практическое значение и широкое применение в технике имеет метод параллельного проецирования, впервые научно разработанный в конце XYIII века французским ученым Гаспаром Монже. Сущность этого метода заключается в том, что данный предмет прямоугольно проецируется на две взаимно перпендикулярные плоскости, одна расположена горизонтально (горизонтальная плоскость проекций ₁), а другая вертикально (фронтальная плоскость проекций ₂). В некоторых случаях прибегают к проецированию на третью плоскость, перпендикулярную к ₁ и ₂ (профильная плоскость проекций ₃). Плоскости ₁,  и ₃ делят пространство на восемь частей, называемых октантами. Каждый октант представляет собой прямоугольный трехгранник, у которого гранями служат части плоскостей проекций, а ребрами -оси координат (рисунок 4).

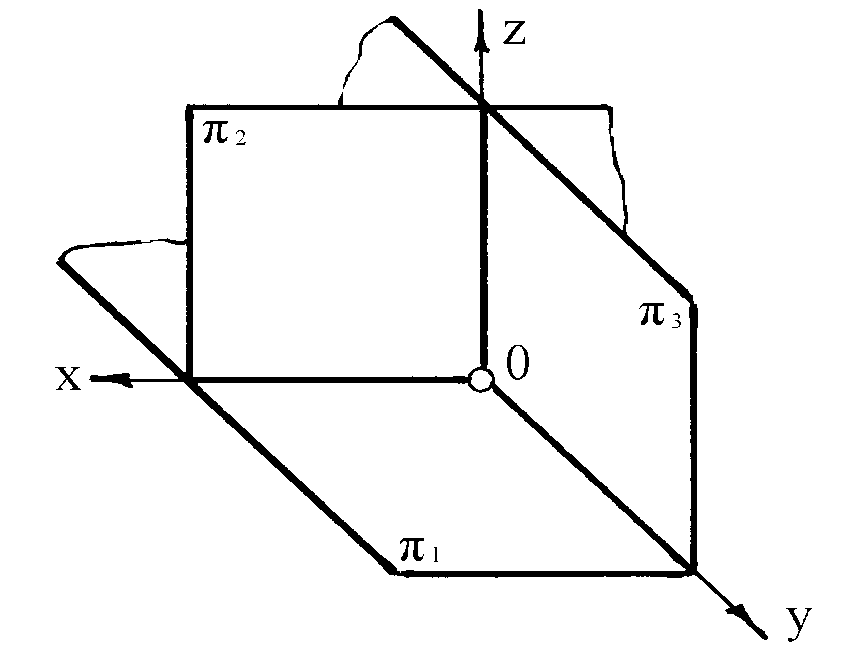
Рисунок 4

 

Ось Х называют осью абсцисс, ось Y - осью ординат, и ось Z – осью аппликат. При этом положительными направлениями осей считают: для оси Х – влево от начала координат, для оси Y- в сторону зрителя от плоскости ₂, для оси Z – вверх от плоскости ₁; противоположные направления осей считают отрицательными.

Между геометрическим образом и ее проекцией существует определенная геометрическая взаимосвязь, заключающаяся в том, что некоторые свойства, относящиеся к оригиналу, сохраняются и в проекциях при любых преобразованиях. Такие свойства называют инвариантными (независимыми). Отметим некоторые свойства проекций геометрических образов при параллельном их проецировании на плоскость.

1. 1.     Проекция точки есть точка А  А'.

2. 2.   Проекция точки, принадлежащей плоскости проекции, совпадает с самой точкой: В  '; В  В'.

3. Проекцией прямой линии (a ) в общем случае является прямая линия: (  a )  (a   ) : l  l'.

4. Если точка А принадлежит линии m, то проекция точки А' принадлежит проекции линии m': A  m  A'  m'.

5. Если линия m принадлежит поверхности , то проекция линии m' принадлежит проекции поверхности ': m    m ' '.

6. Если точка А принадлежит поверхности , то проекция точки принадлежит проекции линии, принадлежащей поверхности:

A    (A'  m'  ')  (A''  m''  '').

Справедливо и обратное утверждение.

Если проекции точки A' и A'' принадлежат соответствующим проекциям линий m' и m'' , которые в свою очередь принадлежат одноименным проекциям поверхности ' и '', то точка А принадлежит поверхности .

7. Если фигура Ф принадлежит поверхности , перпендикулярной плоскости проекции ', то ортогональная проекция этой фигуры Ф' принадлежит следу поверхности h_:

(Ф   )  (   ' )  Ф'  h_.

8. Если фигура Ф принадлежит плоскости , параллельной плоскости проекций ', то ортогональная проекция этой фигуры на плоскость ' конгруэнтна самой фигуре: (Ф   )  (   ' )  Ф'  Ф.

9. Если АВС прямой и сторона ВС этого угла параллельна плоскости

проекций ', а сторона ВА не перпендикулярна плоскости ', то ортогональная проекция угла на плоскость '  А'В'С' = 90^о: (АВС = 90⁰)  ([BC)  ', [BA  ')  А'В'С' = 90^о.

10. Если точка К есть результат пересечения прямых a и b, то ортого - нальная проекция этой точки определяется пересечением ортогональных проекций этих прямых:

К = (a  b)  K₁ = (a₁  b₁)  K₂ = (a₂  b₂).

11. Если прямые a и b параллельны между собой и не перпендикулярны плоскости проекций ', то параллельны и их ортогональные проекции на эту плоскость:

(a  b)  (a  ')  (a'  b').

12. Если отрезок [АВ] параллелен отрезку [СD], то отношение длин отрезков равно отношению длин их ортогональных проекций: [АВ]  [СD]  АC  CB = A₁C₁   C₁D₁.

13. Если точка С принадлежит отрезку [АВ], то отношение [АС] к [СВ] равно отношению их проекций:

С  [АВ]  АС  СВ   А₁С₁   С₁В₁.

 

 

Вопросы для самопроверки

 

1. Какие геометрические элементы включает в себя аппарат проецирования?

2. В каком случае проекция точки будет совпадать с самой точкой-оригиналом?

3. 3.     Какие методы проецирования вы знаете?

4. 4.     Перечислите свойства центрального проецирования.

5. Укажите свойства, общие для центрального и параллельного проецирования.

6. 6.     Назовите свойства, присущие только параллельному проецированию.

7. Какими полами плоскостей проекций ограничены четверти пространства: первая, вторая, третья и четвертая?

8. Как называются и обозначаются основные плоскости проекций?

9. 9.   Как читается теорема о проецировании прямого угла?

2 Точка

 

 

Точка как математическое понятие не имеет размеров. В геометрии под точкой целесообразно понимать физический объект, имеющий линейные размеры. Условно за точку можно принять шарик с бесконечно малым радиусом.

Точки пространства обозначают прописными буквами латинского алфавита или арабскими цифрами: A, B, C, D и т.д. и 1, 2, 3, … Проекции точек обозначаются теми же буквами, что и оригинал, с добавлением нижних индексов соответствующих плоскостей проекций: А₁, В₁, …, А₂, В₂, …,1₁, 1₂… и т.д.

Линия пересечения плоскостей проекций называется осью проекций. Координатами некоторой точки являются числа: они выражают длины отрезков координатных осей, измеренные некоторой установленной единицей длины (в инженерной графике за единицу длины принят миллиметр).

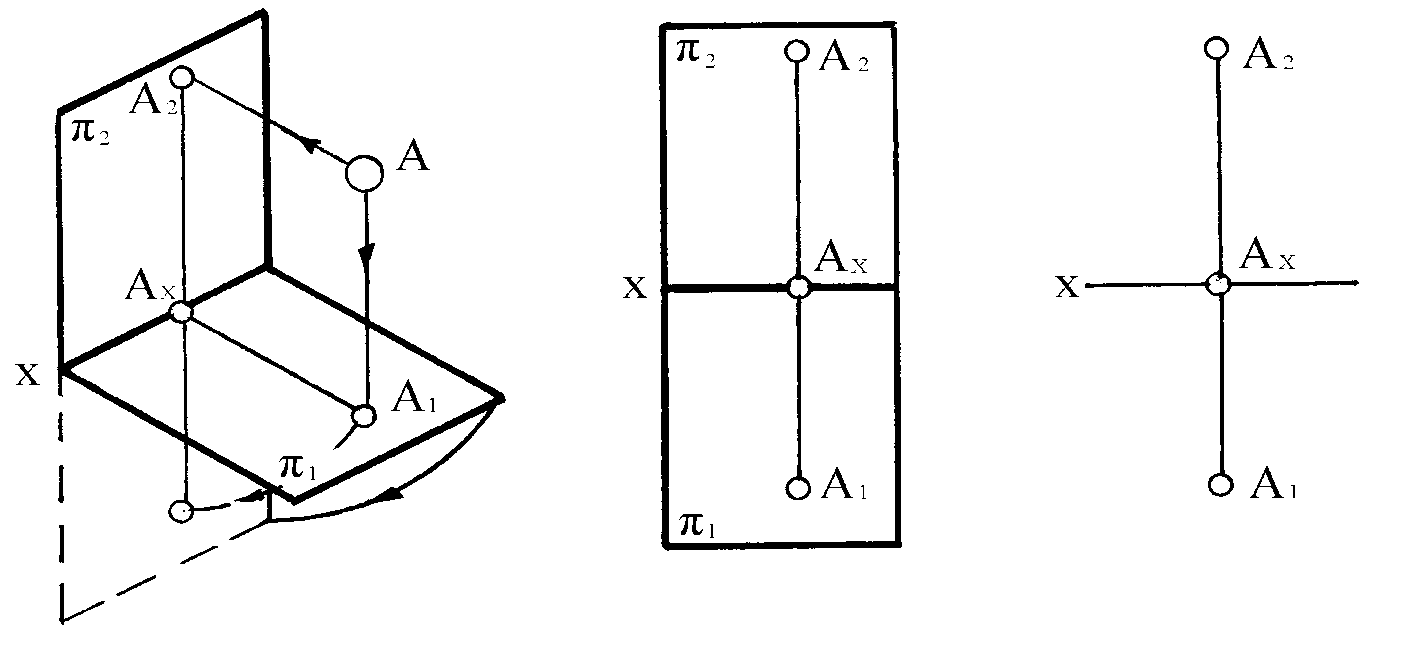
Представим в пространстве некоторую точку А в системе двух взаимно перпендикулярных плоскостей проекций ₁ и ₂ (рисунок 5, а). Чтобы построить проекцию точки А на плоскости ₂, проведем через точку А проецирующую прямую (АА₂  ₂) и отметим точку А₂ (фронтальная проекция точки А), ее пересечения с этой плоскостью. Проведя проецирующую прямую через точку А (АА₁  ₁) в ее пересечении с плоскостью ₁, получим А₁ (горизонтальная проекция точки А).

 

а) б) в)

 

Рисунок 5

 

Опустим перпендикуляр из А₂ на прямую Ох; он пересечется с ней, а, следовательно, с плоскостью ₁ в точке А_х. Опустив перпендикуляр из А₁ на прямую

Ох, мы найдем ту же точку А_х. Отрезок АА₂ = А₁А_х представляет собой расстояние от точки А до плоскости ₂. Отрезок А₂А_х = АА₁ является расстоянием от точки А до плоскости ₁. Проецирующие прямые АА₁ и АА_{2 ,} исходящие из точки А, задают плоскость, которую называют проецирующей плоскостью, она перпендикулярна плоскостям проекций ₁ и ₂ и оси проекций Ох.

Положение точки в пространстве вполне определяется ее ортогональными проекциями на две плоскости проекций.

Повернем плоскость ₁ вокруг оси Ох до совмещения с ₂, как показано на рисунке 5, а. Вместе с плоскостью переместится и точка А₁, а также все другие точки поля проекций ₁. В результате (рисунок 5, б) плоскость чертежа станет носителем двух полей проекций –  ₁ и ₂. Проекции А₁ и А₂ точки А расположены на одном перпендикуляре к оси проекций. Такой перпендикуляр (А₁А₂) называется линией проекционной связи. Чертеж, плоскость которого является носителем двух полей проекций, расположенных так, что линии связи перпендикулярны оси проекций, называется эпюром или эпюром Монжа. Без обозначения плоскостей ₁ и ₂ этот чертеж приведен на рисунке 5, в.

Для решения ряда задач бывают необходимы три и более изображений. Поэтому вводят дополнительные плоскости проекций. Наиболее часто используют третью плоскость проекций (₃), перпендикулярную к двум данным:

₃  ₁, ₃  ₂ - называемой профильной плоскостью проекций (рисунок 6, а).

а) б)

Рисунок 6

Она пересекается с плоскостью ₁ по линии Y, а с плоскостью ₂ – по линии Z.

Чтобы построить профильную проекцию (А₃) точки А на плоскости ₃, необходимо через точку А провести прямую, перпендикулярную ₃. В пересечении этой прямой с ₃ определится точка А₃. Перпендикуляры, опущенные из А₁ и А₃ на ось Y, пересекаются с нею в точке А_y; перпендикуляры, опущенные из А₂ и А₃ на ось Z, пересекаются с нею в точке А_z. Расстояние точки А от плоскости ₁ измеряется отрезком А₂А_х = АА₁, расстояние от плоскости ₂ – отрезком А₁А_х = АА₂, расстояние от ₃ – отрезком А₁А_y = АА₃.

Чтобы перейти к чертежу (рисунок 6, б), на котором все три поля проекций совмещены с одной плоскостью, повернем плоскость ₃ вокруг оси Z, а плоскость ₁ – вокруг оси Х до совмещения с плоскостью ₂. Одновременно переместятся и точки А₁ и А₃. Построение профильной проекции (А₃) точки А по фронтальной и горизонтальной проекциям показано на рисунке 6, б. Можно воспользоваться дугой окружности радиусом ОА_y или прямой, проводимой из точки А_y под углом 45^о, или с помощью постоянной прямой чертежа (). Отметим, что горизонтальная проекция точки А определяется абсциссой Х и ординатой Y; ее фронтальная проекция - абсциссой Х и аппликатой Z, а профильная проекция – ординатой Y и аппликатой Z.

Таким образом, по двум ортогональным проекциям точки можно определить все три ее координаты; по трем координатам точки можно построить ее проекции (комплексный чертеж точки).

Как отмечалось выше, три плоскости проекций делят пространство на восемь частей, называемых октантами. В общем случае точка может быть расположена в любом октанте. Плоскости ₁ и ₂ при пересечении образуют четыре двугранных угла; их называют квадрантами или четвертями пространства. Ось Х делит плоскости ₁ и ₂ на полуплоскости. Фронтальная плоскость (₂) состоит из верхней и нижней полуплоскостей, а горизонтальная плоскость (₁) – из передней и дальней полуплоскостей.

Принято считать, что зритель всегда находится в первой четверти пространства (условно – на бесконечно большом расстоянии от плоскостей проекций), плоскости же проекций непрозрачны, поэтому видимы только точки, расположенные в первой четверти, а также на полуплоскостях ₁ и ₂.

По отношению к плоскостям проекций точка может занимать общее положение, т.е. находиться вне каждой из них (рисунок 5, 6), и частное положение – находиться на одной из плоскостей, сразу на двух плоскостях проекций и одновременно на трех. Если точка находится на одной из плоскостей проекций, то две из трех проекций точки находятся на осях проекций. На рисунке 7

 

 

изображена точка А, принадлежащая, фронтальной плоскости проекций, точка В – горизонтальной, С – профильной. В этом случае две из проекций точки будут на осях – А₁ и А₃, В₂ и В₃, С₁ и С₂, а третья - на соответствующем поле проекций и будет совпадать с самой точкой A₂  А, В₁  В и С₃  С.

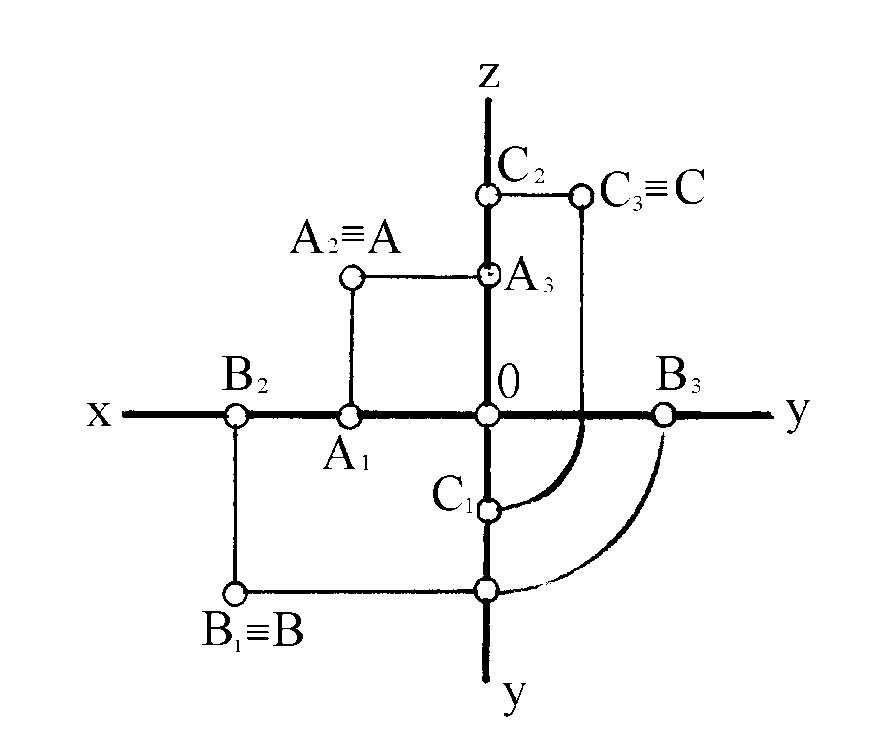
Рисунок 7

 

Точка, находящаяся одновременно на двух плоскостях проекций, изображена на рисунке 8. Так, например, точка D принадлежит плоскостям ₁ и ₂, т.е. лежит на оси Х. Две проекции D₁ и D₂ совпадают с самой точкой D, третья проекция D₃ находится в точке начала координат (О).

 

Рисунок 8 Рисунок 9

Точка Е принадлежит плоскостям ₂ и ₃, т.е. лежит на оси Z. Две проекции Е₂ и Е₃ совпадают с самой точкой Е, горизонтальная проекция (Е₁) точки Е находится в точке начала координат (О).

Точка, лежащая на трех плоскостях проекций, есть начало координат О.

Точки могут принадлежать одна другой, такие точки называют двойными. На чертеже будут совпадать одноименные проекции этих точек, например, точек А и В на рисунке 9.

Точки могут не принадлежать одна другой. В этом случае на чертеже не совпадают одноименные проекции этих точек, например точек С и D (рисунок 9).

В частном случае, если у несовпадающих точек совпадают одни из одноименных проекций (например, горизонтальные проекции точек Е и F на рисунке 9), по их несовпадающим проекциям можно определить, какая из них находится дальше от соответствующей плоскости проекций. Так, например, точка Е расположена выше точки F, т.е. дальше от плоскости _1, чем точка F, а следовательно, относительно горизонтальной плоскости проекций (₁), точка Е видима, а точка F невидима. Точки Е и F называются конкурирующими.

Таким образом, положение точки в пространстве вполне определяется ее ортогональными проекциями на две плоскости проекций.

Точка в пространстве удалена от плоскостей проекций ₁, ₂ и ₃ на величины удаления от оси соответственно ее горизонтальной, фронтальной и профильной плоскости проекций. Горизонтальная и фронтальная проекции любой точки предмета располагаются на одной линии связи, перпендикулярной к оси проекций Ох, фронтальная и профильная проекции точки – на одном перпендикуляре к оси Оz , горизонтальная и профильная – на одном перпендикуляре к оси Оy.

По расположению проекций точки относительно плоскостей проекций можно судить о положении точки в пространстве, т.е. можно установить, на каких расстояниях от плоскостей проекций и в каких октантах находится точка. На рисунке 10 показаны точки, принадлежащие разным углам пространства, а на рисунке 11 дан эпюр этих точек.

Точка А находится в первом октанте, горизонтальная проекция (А₁) точки А лежит под осью проекций Х, а фронтальная проекция (А₂) – над осью проекций Х.

Точка В находится во втором октанте, обе ее проекции В₁ и В₂ расположены над осью проекций Х.

Точка С находится в третьем октанте, горизонтальная ее проекция С₁ расположена над осью проекций Х, а фронтальная проекция С₂ – под осью проекций.

Точка D находится в четвертом октанте, обе ее проекции D₁ и D₂ расположены под осью проекций Х.

Точка Е принадлежит плоскости проекций, одна ее проекция совпадает с самой точкой, а другая лежит на оси. Если точка инциндентна плоскости проекций, то одна ее проекция инциндентна оси Х. Вторая проекция может быть расположена как выше, так и ниже оси в зависимости от того, какой полу-

плоскости принадлежит данная точка. Так, точка Е лежит на дальней горизонтальной полуплоскости. Горизонтальная проекция (Е₁) точки Е расположена выше оси Х, фронтальная проекция Е₂ – на оси Х и совпадает с самой точкой: Е  Е₂. Точка F лежит на передней горизонтальной полуплоскости.

 

Рисунок 10

 

 

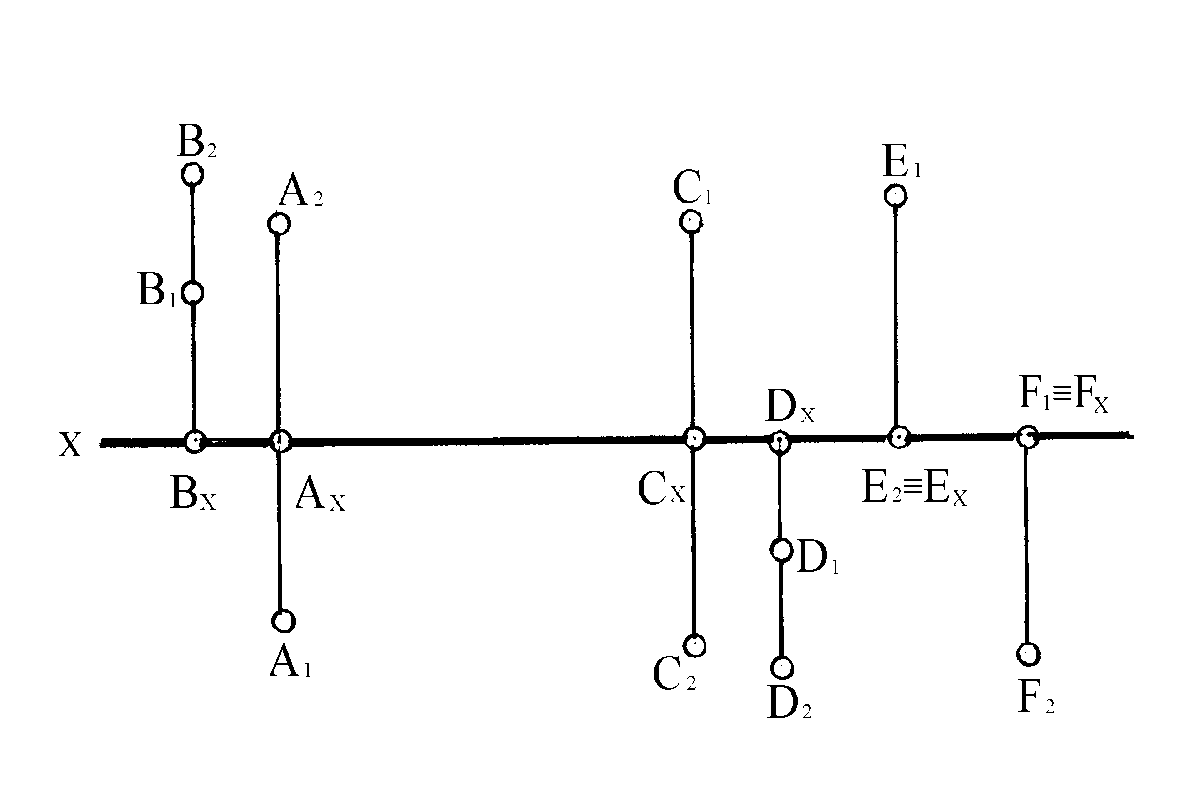
Рисунок 11

На рисунке 12 показаны точки К и U, одинаково удаленные от плоскости проекций ₁ и ₂. Данные точки принадлежат биссекторным плоскостям – плоскостям, делящим углы пространства пополам.

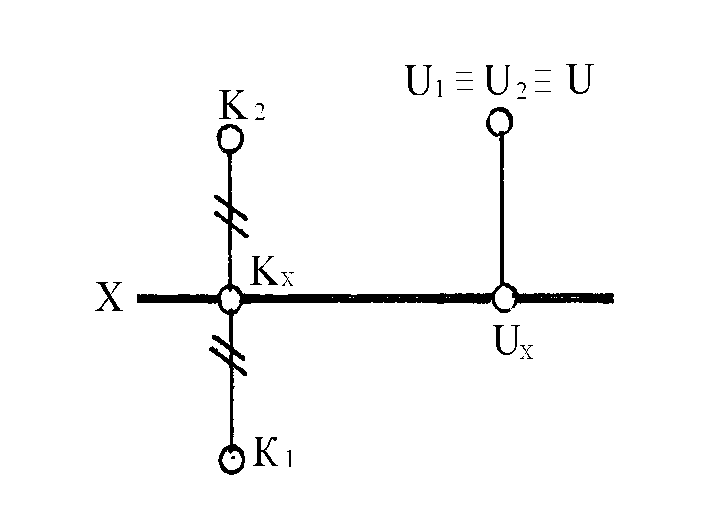
Рисунок 12

 

Плоскость, делящая первый и третий углы пространства пополам, называют первой биссекторной плоскостью. Плоскость, делящую второй и четвертой углы пространства пополам, называют второй биссекторной плоскостью.

Точка К принадлежит первой биссекторной плоскости и находится в первом октанте, а точка U принадлежит второй биссекторной плоскости и находится во втором октанте.

 

 

 

Вопросы для самопроверки

 

 

1. Как принято обозначать точки пространства?

2. Как обозначают проекции пространственной точки и по какому признаку их различают между собой?

3. Как могут быть расположены на эпюре проекции одной и той же пространственной точки относительно оси проекций?

4. Почему одна проекция точки не определяет ее положение в пространстве?

5. Что называется линией проекционной связи?

6. В каких четвертях пространства координата Z точки положительна, отрицательна?

7. В каких четвертях пространства координата Y точки положительна, отрицательна?

8. Что такое октанты?

9. Какой октант имеет отрицательное направление всех осей?

10. Как по комплексному чертежу узнать, является ли точка точкой частного положения?

11. Какие знаки имеют координаты X, Y, Z точки, находящейся в I, II, III,…,YIII октанте?

12. Какие координаты на эпюре определяют горизонтальную и фронтальную проекции точки?

3 Прямая

 

 

Известно, что линию вполне определяют две ее точки, то на комплексном чертеже всякая прямая l может быть задана проекциями двух ее точек. Для прямых линий используются следующие обозначения:

(АВ) – прямая, проходящая через точки А и В;

[AB) – луч с началом в точке А;

[АВ] – отрезок прямой, ограниченной точками А и В.

Линии, произвольно расположенные по отношению к плоскости проекций, могут обозначаться и строчными буквами латинского алфавита: a, b, c,…, l, m, n,…и т.д.

 

 

3.1 Положение прямой линии относительно плоскостей проекций

 

 

Относительно плоскостей проекций прямая линия может занимать различное положение:

• -         не параллельно ни одной из плоскостей проекций;

- параллельно одной из плоскостей проекций (прямая линия может и принадлежать этой плоскости проекций);

- параллельно двум плоскостям проекций, т.е. перпендикулярно третьей.

Прямую линию (АВ), не параллельную ни одной из основных плоскостей проекций (рисунок 13), называют прямой общего положения.

 

Рисунок 13

 

Прямая линия может занимать относительно плоскостей проекций особые (частные) положения. Прямые линии, параллельные одной из плоскостей проекций, называют прямыми уровня. Название их зависит то того, какой плоскости они параллельны.

Прямая линия (CD), параллельная (₁) горизонтальной плоскости проекций (рисунок 14), называется горизонтальной прямой и обозначается буквой ” h”.

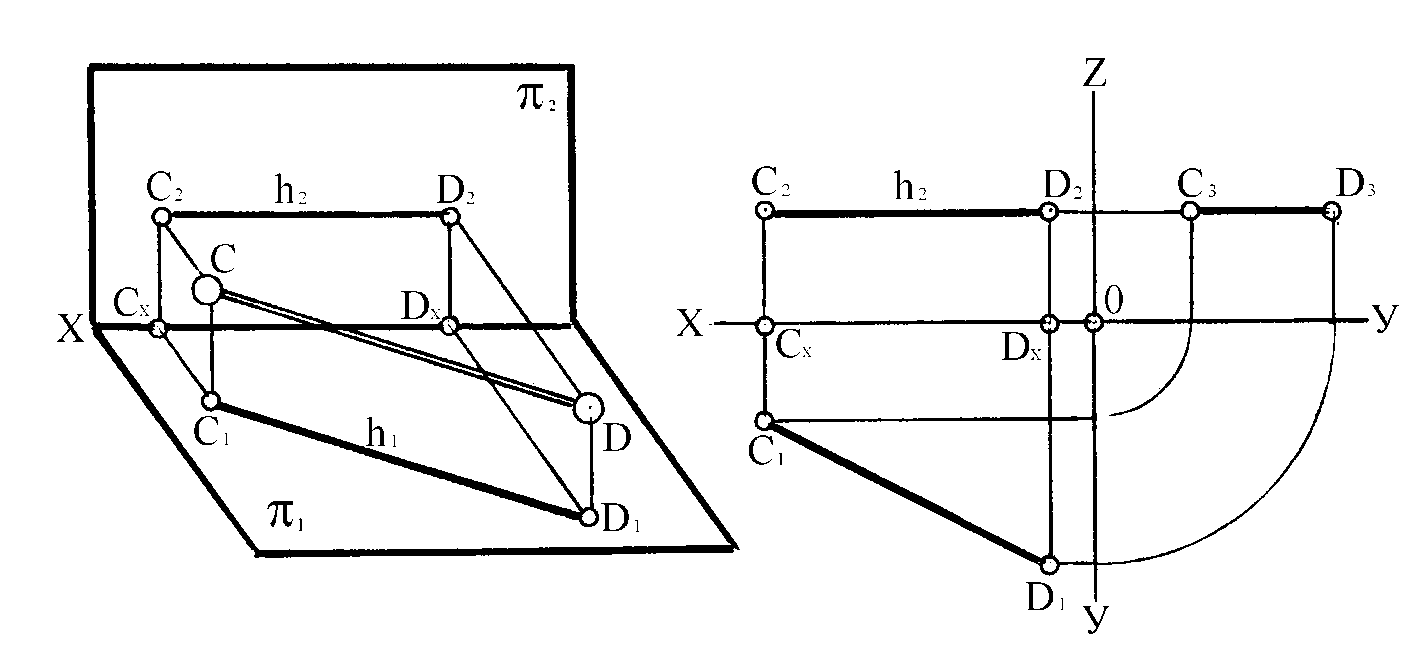
Рисунок 14

 

Фронтальная ее проекция C₂D₂ параллельна оси Х, горизонтальная проекция C₁D₁ может занимать произвольное положение и равна самому отрезку:

C₁D₁ = CD.

Прямая линия (EF), параллельная (₂) фронтальной плоскости проекций (рисунок 15), называется фронтальной прямой и обозначается буквой “f ”.

 

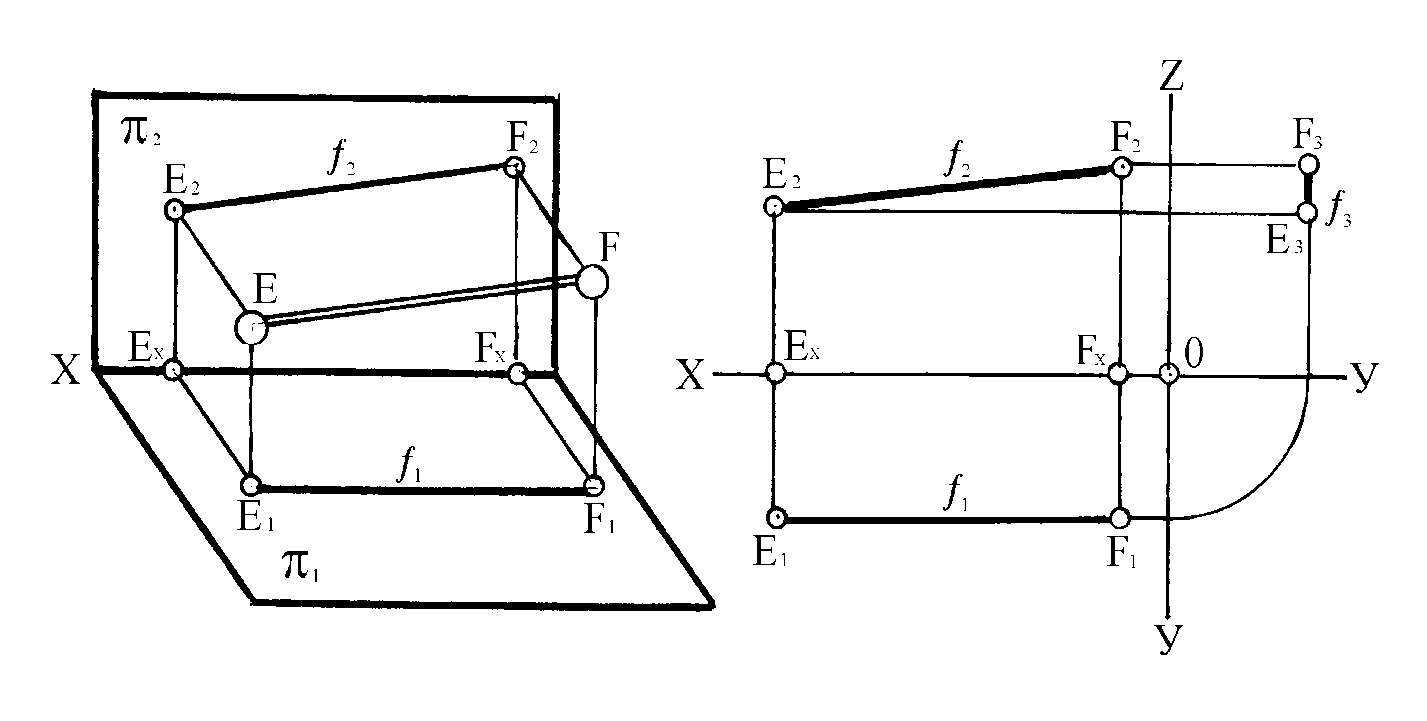
Рисунок 15

Горизонтальная ее проекция E₁F₁ параллельна оси Х, а фронтальная проекция E₂F₂ может занимать произвольное положение и равна самому отрезку: E₂F₂ = E₂F_2.

Прямая линия (MN), параллельная (₃) профильной плоскости проекций (рисунок 16), называется профильной прямой и обозначается буквой ”p”. Горизонтальная (M₁N₁) и фронтальная (M₂N₂) проекции прямой MN располагаются на одном перпендикуляре к оси проекции Х, профильная проекция (M₃N₃) занимает произвольное положение и равна самому отрезку: M₃N₃ = MN.

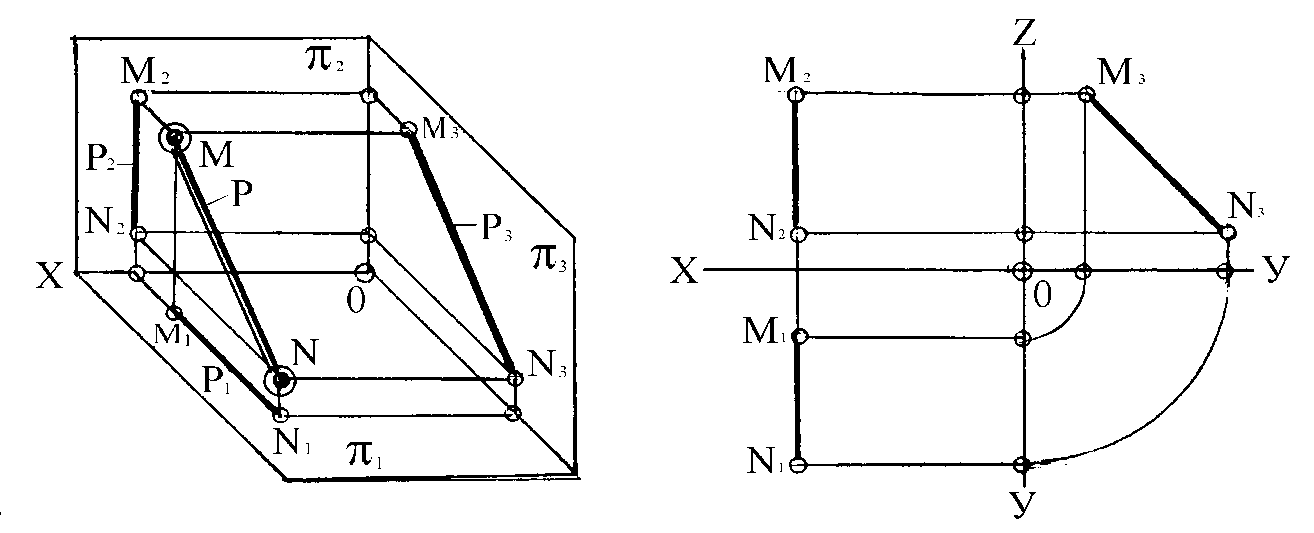
Рисунок 16

 

Прямые линии, перпендикулярные к плоскостям проекций, называются проецирующими. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых линий одна проекция представляет собой точку, а две другие проекции параллельны самой прямой и совпадают на чертеже с направлением связи (рисунок 17).

Прямая линия (АВ), параллельная плоскостям ₂ и ₃, т.е. перпендикулярна к плоскости _1, называется горизонтально-проецирующая прямая (рисунок 17, а). Такая прямая проецируется на плоскость ₁ в точку, а ее фронтальная проекция перпендикулярна оси Х.

Прямая линия (СD), параллельная плоскостям ₁ и ₃, т.е. перпендикулярна к плоскости _2, называется фронтально-проецирующая прямая (рисунок 17, б). Эта прямая проецируется на плоскость ₃ в точку, а ее горизонтальная проекция перпендикулярна оси Х.

Прямая линия (EF), параллельная плоскостям ₁ и ₂, т.е. перпендикулярна к плоскости ₃, называется профильно-проецирующая прямая (рисунок 17, в).

Эти прямые линии могут принадлежать плоскости проекции.

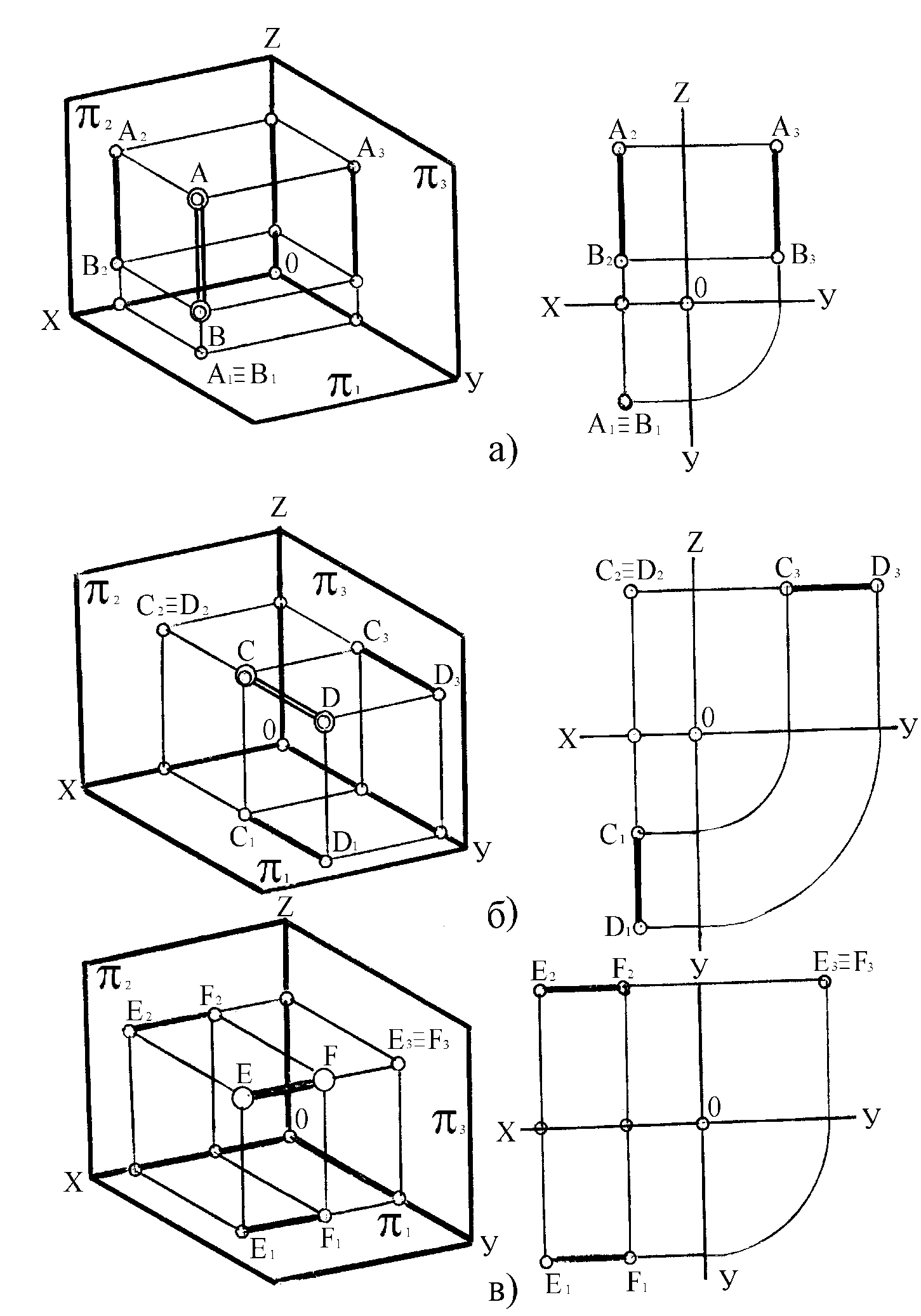
Рисунок 17

Характерным признаком для эпюра, на котором изображена такая прямая линия, будет принадлежность одной из проекций прямой оси. На рисунке 18 показаны проекции прямых линий h, f, p. Прямая линия h принадлежит горизонтальной плоскости проекций: h  ₁ (рисунок 18, а.).

Прямая линия f принадлежит фронтальной плоскости проекции: f  ₂. Прямая линия р принадлежит профильной плоскости проекций: р  ₃. Прямые линии h, f, p являются нулевыми горизонталью, фронталью и профильной прямыми.

Две точки, лежащие на одной проецирующей прямой, называются конкурирующими. Конкурирующие точки помогают определить видимость отдельных элементов предметов на данной плоскости проекций.

Из двух горизонтально-конкурирующих точек А и В (рисунок 17) на плоскости ₁ видима та, которая выше, т.е. точка А, а вторая точка В оказывается под точкой А.

Из двух фронтально-конкурирующих точек C и D (рисунок 17) на плоскости ₂ видима та, которая ближе к наблюдателю, т.е. точка D, а точка С невидима, так как расположена за точкой D.

Из двух профильно-конкурирующих точек E и F (рисунок 17) на плоскости ₃ видима та, которая левее, т.е. точка Е.

 

 

 

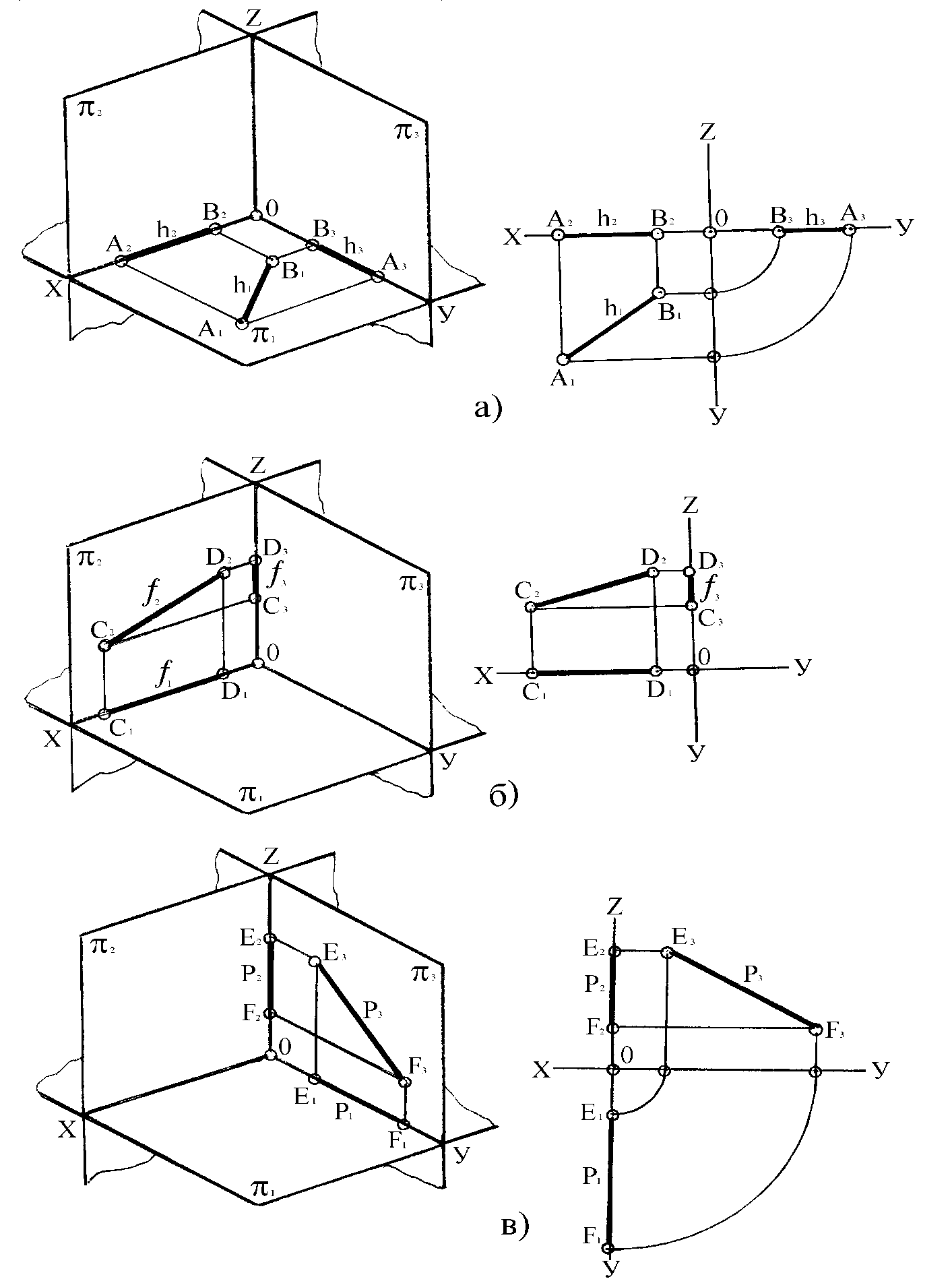
Рисунок 18