main

Это аналогично условию:

1 ( ) < ( 2, ) − ( ( 1, )

(22)

2 ( ) > ( 2, ) − ( ( 1, )

Если ( ) = ( 2, ) − ( ( 1, ), тогда кратчайший пусть может проходить через любой проход. С = max{ {0, . . . , }} : ( ) <

( 2, ) − ( ( 1, )} зачение целевой функции для точки примет вид:

Значения и в формуле (23) неизвестны, так как неизвестна точка оптимального размещения. Следовательно все возможные значения = 1, 2 и

= 0, . . . , мы должны протестировать в алгоритме 1 и найти глобальный оптимум нашей функции. Данные рассуждения приводят нас к следующему алгоритму:

21

Алгоритм 1. Для решения задачи Ферма–Вебера с линейными барьерами и

двумя проходами.

1.Для = 1, 2

(a)Пусть 1, 2 и ̸= .

(b)Пусть ( ) = ( , 1) − ( , 2);

(c)Отсортируем существующие точки размещения так, чтобы:

(1) ≤ · · · ≤ ( ).

(d)Для значений = 0 : , выполнить условия:

ii.Определим оптимальное решения классической задачи Вебера

сточками размещения = { 1, 2, , . . . , } и с весами

определенными в (a).

iii.Для Определим ¯( ) = ( ) + .

Сложность алгоритма 1 равна ( log + ), где = 1 + 2 —

множество источников сырья и/или рынков сбыти, а значение ( ) равно времени решения задачи Ферма–Вебера без барьеров. На шаге 3 источники сырья и/или рынков сбыта, должны быть отсортированы, а на шаге 4 должна быть решена раз задача Ферма–Вебера без барьеров с временной сложностью

( ).

Данный алгоритм был изложен в работе [11], алгоритм для более двух проходов не сильно отличается от алгоритма для двух проходов, его сложность

равна ( ( log( ) + ( + −1) ), где N — число проходов.

−1

22

4.Решение задачи на размещение предприятия

Вследующем алгоритме объявляются точи размещения (где = 1, 2, а = 1, 2, 3) и проходы , далее считается значение .

Объявление данных и посчет ≡

Ex = {{{4.5, 7}, {5, 7}, {10, 7.5}}, {{3, 3}, {6, 1}, {8.5, 4}}};

P= {{4, 5}, {9, 5}};

For[i = 1, i <= 2, i++,

For[m = 1, m <= 3, m++,

Dd[[i, m]] = N[Norm[Ex[[i, m]] - P[[1]]] - - Norm[Ex[[i, m]] - P[[2]]]];

]

]

3

Шесть источников ресурсов и/или рынков сбыта, которые расположе-

ны на обеих сторонах линии с координатами, весами и значением

представлены в Таблице 1.

Таблица 1 – Источники силы притяжения и значения

Следующий алгоритм генерирует необходимые веса точек ( ) для составления восьми подзадач Ферма–Вебера .

Генерация значений ( ) для восьми подзадач ≡

w = {{0, 1, 2, 2, 0}, {0, 2, 3, 2, 0}};

23

For[i = 1, i <= 2, i++,

For[k = 1, k <= 4, k++,

wP1[[i, k]] = Sum[w[[i, j]], {j, 1, k}]; wP2[[i, k]] = Sum[w[[i, l]], {l, k + 1, 5}];

]

]

3

Далее, получив необходимую информацию, можно приступить к ре-

шению восьми подзадач, в данном алгоритме использовалась встроенная

функция нахождения минимума.

Алгоритм решения восьми подзадач Ферма–Вебера ≡

For[i = 1, i <= 2, i++,

For[k = 1, k <= 4, k++,

f[[i,k]]=Sum[Norm[Ex[[i, j]] - {x, y}]*w[[i, j]], {j, 1, 3}] g[[i,k]]=Norm[P[[1]] - {x, y}]*wP1[[i, k]] +

Norm[P[[2]] - {x, y}]*wP2[[i, k]], {x, y}];

X[[i,k]]=[Minimize[f[[i,k]] + g[[i,k]], {x, y}]];

]

]

3

В Таблице 2 приведена вся необходимая информация о подзадачах.

Таблица 2 – Оптимальное решение восьми подзадач

24

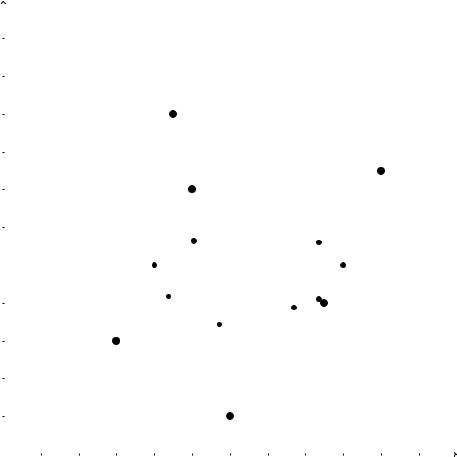
Рисунок 1

ного оптимума со значением ( * ) = ¯( * ) = 48.47.

25

Заключение

Исследование этого вопроса имеет большое значение для экономики государства, так как модель Ферма–Вебера с барьерами, может успешно применятся при планоровке размещения нового перерабатывающего предприятия. Метод, разобранный в данной работе, позволяет светси задачу размещения предприятия с линейными барьерами, к решению конечного числа оптимизационных задач выпуклой оптимизации, решение которых современными пакетами не составляет большой сложности.

Практическое же решение задачи c двумя проходами, позволяет увидеть алгоритм решения задач Ферма–Вебера с барьерами в действии. И понять его практическую ценность.

26

Список литературы

[1]Гранберг, А.Г. Основы региональной экономики // М. Изд-во ВШЭ, 2004.

[2]Handbook of regional and urban economics. Vol 1. Regional economics. Ed. By NijkampA // North Holland, 1986.

[3]Kuhn H.W. On a pair of dual nonlinear programs // In J. Abadie, editor, Nonlinear Programming. North Holland, 1967.

[4]Kuhn H. W. A note on Fermat’s Problem // «Mathematical Programming»,4 (1973),pp 98-107.

[5]Reuven C. Noniterative Solution of Some Ferma–Weber Location Problems

//The Raymond & Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, 2011.

[6]Weber A. Uber den Standort den Industrie // University of Chicago Press, Chicago, III, USA, 1909.

[7]Katz I.N. and Vogl S.R. A Weiszfeld algorithm for the solution of an asymmetric extension of the generalized Fermat location problem // Computer & Mathematics with Applications, vol. 59, no 1,pp. 399-410, 2010.

[8]Llambay A. B., Llambay P. B., Pilotta E. A. On characterization the solution for the Fermat–Weber location problem // Serie «A», Trabajos de Matematica, Republica Argentina, 2009.

[9]Drezner Z. A note on the Weber location problem // Annals of Operations Research, vol. 40, no 1–4, pp. 153–161, 1992.

[10]Drezner Z. A note on accelerating the weiszfeld procedire // Location Science, vol. 3, no. 4, pp. 275–279, 1995.

[11]Klamroth K. Single-Facility Location Problems with Barriers // Springer Series in Operations Research, 2002.

27