Контрольные вопросы

1. Как выражается передаточная функция эквивалентного звена для случаев последовательного, параллельного и встречно-параллельного соединения звеньев?

2. В каких случаях нужно пользоваться структурными преобразованиями?

3. В каких случаях нужно пользоваться формулой Мейсона?

4. В чём преимущество представления сложной системы управления в виде сигнального графа?

5. Можно ли по сигнальному графу восстановить структурную схему системы управления?

5. Частотные характеристики. Амплитудно-фазовая характеристика. Связь амплитудно-фазоВой характеристиКи с передаточной функцией. Логарифмические частотные характеристики

Частотные характеристики описывают передаточные свойства звеньев (элементов) и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием.

Рассмотрим прохождение гармонического сигнала через элемент (рис. 18).

Рис. 18. Прохождение гармонического сигнала через элемент

Входной гармонический сигнал преобразуется как по модулю (становится равным ), так и по фазе (рис. 19). Фазовый сдвиг определяется величиной, определяемой выражением:

. (64)

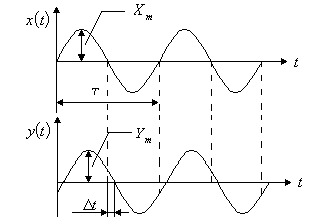
Рис. 19. Преобразование гармонического сигнала по модулю и по фазе

Амплитуда выходного сигнала зависит от амплитуды входного сигналаи от частоты, то есть, фазовый сдвиг зависит только от частоты, то есть.

Более удобно при описании передаточных свойств элемента рассматривать отношение амплитуд выходного и входного сигналов.

Зависимость отношения амплитуд выходного и входного сигналов от частоты называется амплитудной частотной характеристикой (АЧХ). Ее обозначают (рис. 20).

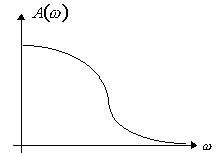
Рис. 20. Амплитудная частотная характеристика

Зависимость фазового сдвига от частоты называется фазовой частотной характеристикой (ФЧХ), и она обозначается (рис. 21).

АЧХ показывает, как хорошо пропускает элемент сигналы различной частоты. ФЧХ показывает, какое отставание или опережение входного сигнала по фазе создает элемент при различных частотах.

Амплитудную частотную и фазовую частотную характеристики можно объединить в одну общую: амплитудно-фазовую частотную характеристику (АФЧХ) или (АФХ) (рис. 22). Она обозначается и представляет собой функцию комплексного переменного, модуль которой равен, а аргумент равен.

АФХ , как и любая комплексная величина, может быть представлена в показательной:

(65)

или в алгебраической форме:

,(66)

где – проекция векторана вещественную ось, а– проекция векторана мнимую ось.

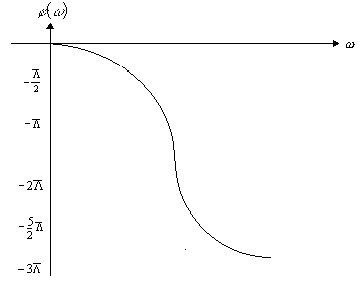
Рис. 21. Фазовая частотная характеристика

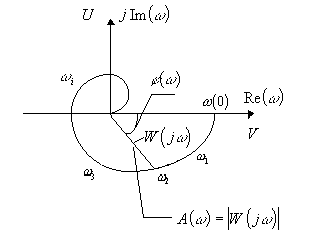
Рис. 22. Амплитудно-фазовая характеристика

называется вещественной частотной характеристикой, а– мнимой частотной характеристикой.

АФХ есть изображение по Фурье импульсной переходной функции:

. (67)

Обратное преобразование Фурье АФХ даст импульсную переходную функцию:

. (68)

Аналитическое выражение для АФХ конкретного элемента можно получить из его передаточной функции подстановкой :

. (69)

Представим передаточную функцию в виде отношения оператора воздействий и собственного оператора:

. (70)

Тогда

, (71)

отсюда

. (72)

Покажем правомерность соотношения (69). Пусть на вход элемента поступает гармонический сигнал , а на выходе получают сигнал.

Выразим , пользуясь формулой Эйлера,

. (73)

Запишем входной и выходной сигнал в виде:

. (74)

. (75)

Учитывая свойство суперпозиции линейного элемента, входная составляющая вызывает составляющую выходного сигнала.

Следовательно, передаточные свойства элемента можно определить только по одной из них:

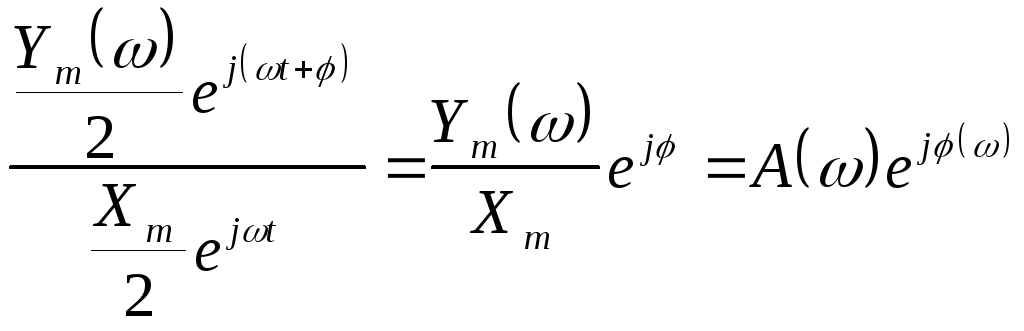(76)

или

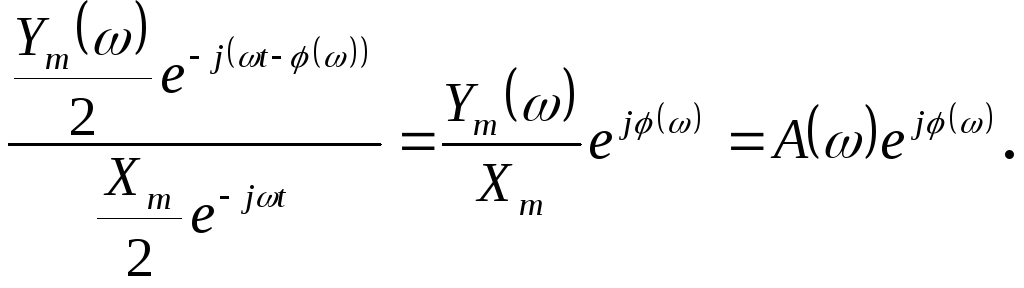(77)

Предположим, что элемент описывается линейным дифференциальным уравнением n-го порядка

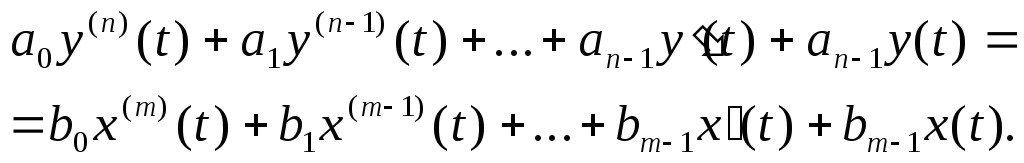(78)

В дальнейшем будем полагать, что на вход элемента поступает сигнал , а на выходе получим сигнал.

Теперь возьмем производные

при, (79)

при(80)

и, подставляя их в дифференциальное уравнение элемента (78), получим

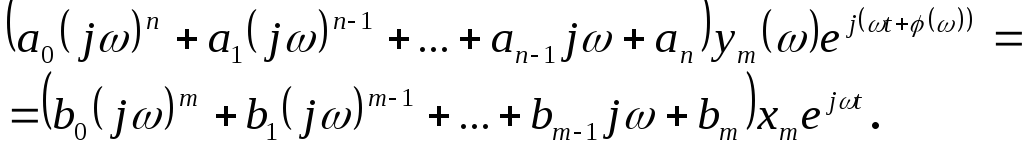(81)

Уравнение (81) представим в виде отношения:

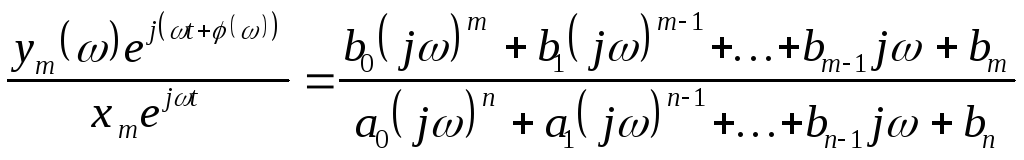(82)

и перепишем с учетом (65) и (76):

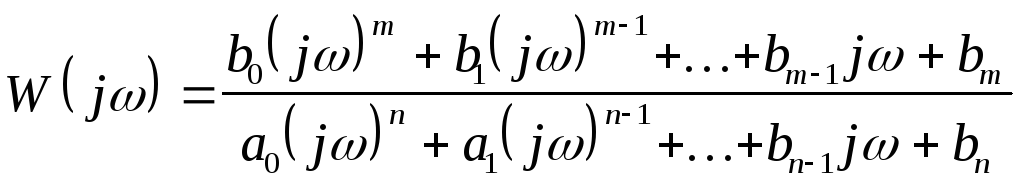. (83)

Теперь преобразуем уравнение (78) по Лапласу и представим его в виде отношения:

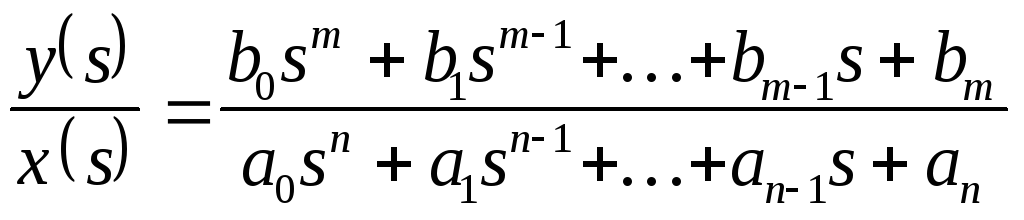. (84)

Учитывая, что

, (85)

и сравнивая выражения (83) с (84), устанавливаем связь амплитудно-фазовой характеристики с передаточной функцией: амплитудно-фазовая характеристика может быть получена из передаточной функции путем подстановки .

Отметим, что элемент (звено или система) называется минимально фазовым, если все корни числителя (нули) и все корни знаменателя (полюсы) в выражении (84) имеют отрицательные вещественные части. Во всех других случаях фазовой сдвиг будет иметь большее значение.