1. Аксиомы Колмогорова

Пусть задано измеримое пространство

1. - вероятность (вероятностная мера) случайного события A

2.

3. Аксиома сложения

Если , , то

4. Аксиома непрерывности

Пусть убывающая последовательность случайных событий

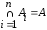, , тогда

Пусть возрастающая последовательность случайных событий

, , тогда

2. Свойства Вероятностей

1. Действительно , ,

2. Действительно , , ,

3. Если , то Действительно , т.к. 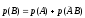. Всегда . Тогда

4. Действительно или

5. Если A, B – произвольные случайные события, то

Действительно

Тогда

.

Тогда

и

6. Если , i=1,2,… - произвольны, то .

Действительно . Если , то , .

Так как , то . Тогда

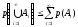
3. Классическое определение вероятности, условие применимости

Пусть пространство элементарных событий Ω конечно. Ω={ω_1,ω_2,…,ω_n}.

Тогда σ – алгебру F составляют все подмножества пространства Ω. Имеем

=Ω

P()==P(Ω)=1 (1)

Пусть AF и m – число ω_iA. Тогда

A= (2)

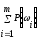P(A)= (3)

Пусть

P()=P()=…=P()=P (4)

Тогда из (1), (4) P =.

Из (3)

P(A) = (5)

(5) – классическое определение вероятности.

- исходы эксперимента, благоприятствующие появлению события A.

Согласно (5), вероятность случайного события равна отношению числа исходов, благоприятствующих появлению этого события к числу всех возможных исходов случайного эксперимента.

Условия применимости формулы для классического определения вероятности.

1. Пространство Ω конечно.

2. Элементарные события пространства Ω равновозможные

P() = P() =…= P()

4. Геометрическое определение вероятности

Пусть задано измеримое пространство . Пусть случайный эксперимент можно интерпретировать как бросание точки в область так, что точка с равной возможностью может попасть в любую часть области 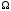и попадание ее в некоторое заданное подмножество А из пропорционально мере этого подмножества. Если , , то

(1)

1. – Геометрическое определение вероятности

5. Условная вероятность, теорема умножения вероятностей. Независимость случайных событий.

Пусть имеются случайные события А, В и .

Определение. Условной вероятностью события А при условии, что произошло событие В называется число

(1)

Аналогично (1) при

(2)

Из (1), (2)

, (3)

(3) -Теорема умножения вероятностей.

Пусть А₁, А₂,…, А_n – случайные события. Тогда

(4)

Определение. Случайные события А, В называются независимыми, если

(5)

Из (3) (5) для независимых событий

,

Определение. Случайные события А₁, А₂,…, А_n называются независимыми в совокупности, если для любых целых , к = 2,3,…,n

(7)

Из независимости в совокупности следует попарная независимость, обратное не всегда верно.

Если случайные события А, В независимы, то независимы и события

, ,