Постановка задачи

 

Рассмотрим диск переменной толщины  с центральным от­верстием,  симметричный относительно срединной плоскости.  Материал диска изотропный, упругий.  Диск нагрет до температуры , переменной по радиусу и постоянной по толщине,  и вращается с угло­вой скоростью . Закон изменения температуры  и зависимость модуля упругости , коэффициента Пуассона  и коэффициента линей­ного расширения  материала диска от температуры предполагаем из­вестными. Располагая этими данными,  можно получить законы измене­ния величин ,  и  по радиусу диска: , , .

Расчетная схема диска, представлена на рис.1.1.

 

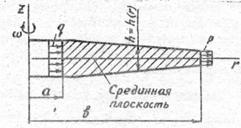
Рис.1.1. Расчетная схема диска

 

При вращении диска возникают массовые силы инерции,  распреде­ленные по его объему и направленные по радиусу от центра.  Интен­сивность этих сил   является функцией радиуса и равна произведе­нию плотности материала диска  на величину центростремительного ускорения , т.е. .

Воздействие на диск присоединенных к нему по наружной поверх­ности  лопаток и узлов их крепления может быть представлено инерционной радиальной нагрузкой.  Ввиду того,  что обычно число ло­паток велико,  будем считать эту нагрузку равномерно распределен­ной по наружной поверхности.  Обозначим интенсивность этой нагруз­ки через .

В результате посадки диска на вал с натягом  (напомним,  что под натягом понимают разность диаметров вала и отверстия) на по­верхностях контакта возникают силы давления.  Предположим,  что эти силы равномерно распределены по контактным поверхностям; интен­сивность их обозначим через  и назовем контактным давлением. Величина контактного давления зависит от величины  натяга  угловой скорости вращения диска .

В основу расчета диска положим два допущения.  Согласно  перво­му принимаем равномерное распределение  напряжений по  толщине дис­ка.  Согласно второму допущению предполагаем, что напряжения в плоскостях,  параллельных срединной плоскости, отсутствуют.  Это позволяет считать напряженное состояние всех точек диска двухос­ным.

Эти допущения были обоснованы путем сопоставления приближен­ного решения с точным, полученным для некоторых частных случаев, и справедливы при условии, что отношение внешнего диаметра диска к его наибольшей толщине больше 4.

Учитывая первое допущение,  заключаем,  что в рассматриваемой постановке  напряжения,  деформации и перемещения в диске являются функциями только радиуса.

Переходим к решению задачи.

Уравнение  равновесия элемента диска

 

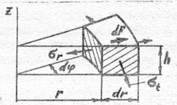
Рис.1.2. Элемент диска

 

Выделим из диска элемент в форме криволинейного шестигранника (рис. 1.2).  В радиальных сечениях по условиям симметрии касатель­ные напряжения отсутствуют,  и возникают лишь нормальные напря­жения,  которые  называются коль­цевыми или окружными и обознача­ются . Таким образом, площадки, лежащие в радиальных сечени­ях, являются главными. Учитывая, что напряженное  состояние диска является плоским (см. второе допущение),  заключаем,  что площадки, лежащие  в окружных сечениях,  также являются главными.  Нормальные напряжения в этих сечениях называются радикальными и обозначаются .

Помимо радиальных и кольцевых внутренних сил к рассматриваемо­му элементу приложена еще и объемная сила  где объем элемента.

 

Рис.1.3. Внутренние усилия в диске

 

Внутренние силы,  возникающие в сечениях диска приводим к его срединной плоскости.  В окружном сечении получаем радиальное усилие интенсивности

на единицу длины окружного сече­ния срединной плоскости (рис.1.3). В радиальном сечении получаем кольцевое усилие интенсивности

на единицу длины радиального се­чения срединной плоскости.

Проектируя силы, действующие на элемент диска,  на радиальное направление,  получим следующее уравнение равновесия:

откуда,  учитывая,  что   и обозначая , устанавливаем,  что .

 

(1.1)

 

 

Остальные уравнения равновесия для элемента выполняются тож­дественно.  Параметр  называют динамическим коэффициентом.

В уравнение равновесия (1.1) входят две неизвестных величины  и , поэтому задача определения внутренних усилий в диске явля­ется статически неопределимой. Для решения ее необходимо рассмот­реть деформации.

Деформации элемента диска

 

Рис.1.4. Перемещения точек элемента диска

 

Рассмотрим элемент диска до и после деформации  (рис.1.4). Перемещения точек диска по условиям симметрии будут происходить в радиальных направлениях,  ради­альное  перемещение  точек  на ра­диусе  обозначим через . Тогда радиальное  перемещение точек на радиусе  будет .  За положительное  на­правление для  примем направ­ление от оси диска обозначим через  и  относительные деформации в диске в радиальном и кольцевом  направлениях и вы­разим их через  перемещение .

Очевидно,  что радиальная деформация

 

(1.2)

 

а кольцевая деформация

 

(1.3)