
Лекция 22. Методы интегрирования
.docЛекция 22. Методы интегрирования.
22.1. Метод замены переменных.
Основную роль в интегральном исчислении играет метод замены переменной (или метод подстановки):
![]() .
(22.1)
.
(22.1)
Предполагается,
что
![]() есть непрерывно дифференцируемая
(имеющая непрерывную производную)
функция на некотором интервале изменения
t,
а
есть непрерывно дифференцируемая
(имеющая непрерывную производную)
функция на некотором интервале изменения
t,
а
![]() – непрерывная функция на соответствующем
интервале или отрезке оси x.
– непрерывная функция на соответствующем
интервале или отрезке оси x.
Докажем (22.1):
![]() .
.
Следовательно,
если ввести подстановку
![]() ,
то получится первообразная от функции
,
то получится первообразная от функции
![]() .
Две первообразные отличаются на некоторую
постоянную C.
(22.1) доказана. ■
.
Две первообразные отличаются на некоторую
постоянную C.
(22.1) доказана. ■
Формулу (22.1) перепишем в удобном виде:
![]() .
(22.1а)
.
(22.1а)
Пример 22.1.
1)
![]() .
.
2)

![]() .
.
3) а)
![]()
![]() .
.
б)
![]() .
.
в)

(доказательство формулы 8 таблицы интегралов лекции 21).
г)
![]()
(доказательство формулы 12 таблицы интегралов лекции 21).
4) а) При
![]()
 .
.
б) При
![]() ,
,
![]() ,
,
 .
.
в) При
![]() ,
,
![]() ,
,
 .
(22.2)
.
(22.2)
г)
![]() .
.
д) При
![]()

![]() ,
,
где последний интеграл вычисляется по (22.2).
Пример 22.2. Вычислить заменой переменных интегралы
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
5)
,
5)
![]() ,
,
6)
![]() ,
7)
,
7)
![]() ,
8)
,
8)
![]() ,
9)
,
9)
![]() ,
,
10)
![]() ,
11)
,
11)
![]() ,
12)
,
12)
![]() ,
13)
,
13)
![]() .
.
22.2. Метод интегрирования по частям.
♦ Теорема 22.1
(формула
интегрирования по частям).
Пусть
![]() и
и
![]() – непрерывно дифференцируемые функции.
Тогда
– непрерывно дифференцируемые функции.
Тогда
![]() .
(22.3)
.
(22.3)
Доказательство.
Имеем
![]() ,
следовательно
,
следовательно
![]() и после интегрирования получаем:
и после интегрирования получаем:
![]() .
Окончательно:
.
Окончательно:
![]() .
.
Постоянную C обычно опускают, так как в правой части формулы интегрирования по частям стоит неопределённый интеграл. ■
Интеграл
![]() может оказаться более простым, чем
может оказаться более простым, чем
![]() .
Большую часть интегралов, вычисляемых
методом интегрирования по частям, можно
разбить на 3 группы:
.
Большую часть интегралов, вычисляемых
методом интегрирования по частям, можно
разбить на 3 группы:
1)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() – многочлен степени m.
При вычислении интегралов этой группы,
необходимо за
– многочлен степени m.
При вычислении интегралов этой группы,
необходимо за
![]() принять
принять
![]() (обратную тригонометрическую функцию
или логарифм) и положить
(обратную тригонометрическую функцию
или логарифм) и положить
![]() .
.
2)
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() – многочлен степени m.
При вычислении интегралов этой группы,
необходимо принять
– многочлен степени m.
При вычислении интегралов этой группы,
необходимо принять
![]() ,
,
![]() .
Необходимо применить интегрирование
по частям m
раз.
.
Необходимо применить интегрирование
по частям m
раз.
3)
![]() ,
,
![]() .
Здесь необходимо применить двукратное
интегрирование по частям, после чего
искомый интеграл выражается сам через
себя и находится из получающегося
линейного уравнения 1‑го порядка.
.
Здесь необходимо применить двукратное
интегрирование по частям, после чего
искомый интеграл выражается сам через
себя и находится из получающегося
линейного уравнения 1‑го порядка.
Пример 22.3.
1)
 .
.
2)
 .
.
3)

![]() ,
,
откуда
![]() .
.
Пример 22.4. 1)
![]()
![]() .
.
2)
 ,
,
![]() – алгебраический многочлен. Применяем
n-кратное
интегрирование по частям. Так как
характер первообразной легко угадывается,
то эти интегралы можно вычислять методом
неопределённых коэффициентов.
– алгебраический многочлен. Применяем
n-кратное
интегрирование по частям. Так как
характер первообразной легко угадывается,
то эти интегралы можно вычислять методом
неопределённых коэффициентов.
Например, для
![]() первообразная имеет вид:
первообразная имеет вид:
![]() ,
где
,
где ![]() .
.
Коэффициенты находим из условия
![]()
![]()
![]() .
.
3)
![]() ;
;
![]() ,
,
![]() ,
,
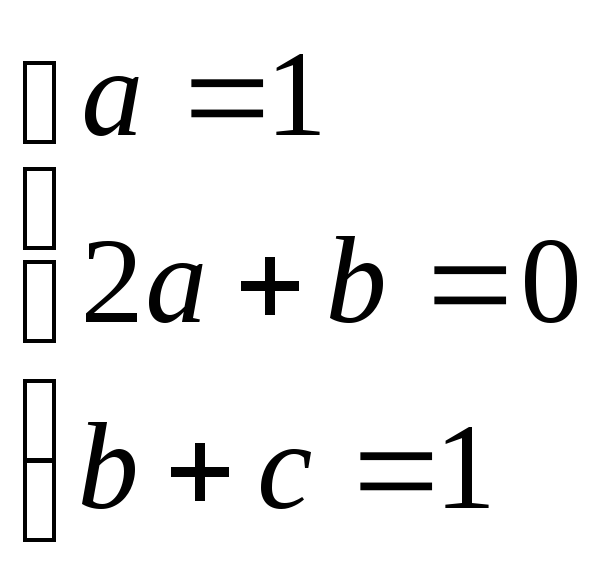

![]() .
.
Пример 22.5. 1)
 .
.
Здесь можно было
поступить наоборот и принять
 .
Далее имеем:
.
Далее имеем:
 ,
,
![]() ,
,
![]() ,
,
![]() .
.
2) Тем же самым способом можно получить, что
![]() ,
,
а можно найти
![]() по связи с
по связи с
![]() .
.
22.3. Некоторые рекуррентные1 формулы.
1)
Метод интегрирования по частям для
интеграла
![]() ,
,
![]() ,
,
![]() приводит к рекуррентному выражению
приводит к рекуррентному выражению
![]() ,
где
,
где

![]() ,
,
и окончательно:
![]() ,
,
![]() .
.
Используя это выражение, можем понизить индекс на единицу, двойку и т.д., что приводит к цепочке формул:
![]() ,
,
![]() ,
,
![]() ,
,
приводящей к
![]() .
.
Пример 22.6.
1)
![]()
![]() .
.
2)
Рассмотрим также интеграл
![]() :
:

 ,
,
то есть
 .
.
Применяя тот же
процесс, приводящий к понижению на
единицу показателя степени в знаменателе
подынтегральной дроби, придём к
![]() .
.
Таким образом, при
![]() и
и
![]() интеграл
интеграл
![]()
![]() берётся в элементарных функциях.
берётся в элементарных функциях.
1 От лат. recurrens – возвращающийся.
