Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Термодинамика ч1 - Сотский А.Б

..pdf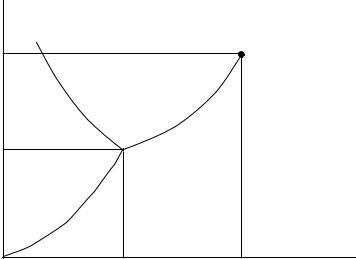

Скачиваний:

Добавлен:

18.04.2015

Размер:

836.09 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Здесь 1, 2, 3 – номера фаз. Решение каждого из уравнений (19.1) и (19.2) дает некоторую кривую на плоскости переменных Р, Т . Но иногда оказы-

вается, что кривые, соответствующие уравнениям (19.1) и (19.2), пересекаются. Формально это означает, что решение системы двух уравнений с двумя неизвестными (19.1) и (19.2) может дать одну, или несколько пар конкретных значений Р и Т.

Мы ограничимся рассмотрением термодинамических систем, для которых система (19.1), (19.2) имеет единственное решение Т0 , Р0 . Точка с

координатами Т0 , Р0 на Т, Р плоскости называется тройной точкой. На-

пример, такая точка может соответствовать равновесию трех фаз вещества

– твердой, жидкой и газовой. В частности, для воды параметры тройной точки таковы:

Т0 = 0.0078 С,

Р0 = 0.006 атм.

Графики кривых равновесия трех фаз для воды качественно изображены на Рис. 19.1. В предыдущем параграфе было показано, что повыше-

Рk

жидкость

твердая

фаза

Р0

газ

0	T0	Tk	T
	Рис. 19.1

ние давления при данной температуре относительно давления фазового равновесия переводит вещество в ту фазу, которой соответствует меньший удельный объем. Минимальный удельный объем среди всех трех фаз воды имеет жидкая фаза, далее следует лед и затем - пар. Отсюда и следует взаимное расположение фаз, которое представлено на Рис. 19.1.

Надо сказать, что тройная точка воды, если она достигнута, является весьма стабильным состоянием. Это обстоятельство используется в технике для получения высоко стабилизированных температур и давлений.

Отметим некоторые особенности графиков на Рис. 19.1. На кривой равновесия фаз жидкость - пар имеется критическая точка с координатами

Тk , Рk . В ней различие между жидкой и газовой фазами исчезает. Кривая

равновесная твердой и газовой фаз, как показывают эксперименты, идет в начало координат, а кривая равновесия жидкой и твердой фаз при Т → 0 уходит в бесконечность.

§ 20. Фазовые переходы второго рода

Исследуя фазовые переходы первого рода, мы выяснили, что при изменении давления или температуры химический потенциал вещества изменяется непрерывно. Однако его производные

∂μ	= −Sɶ,	∂μ	= Vɶ	(20.1)
	= −Sɶ,		= Vɶ	(20.1)
∂T P		∂P T

изменяются скачком. Это видно, в частности, из Рис. 18.1 и 18.2, где зависимости μ(P) при фиксированной температуре и μ(T ) при фиксированном

давлении имеют изломы в точках фазового перехода.

Но в природе существуют также фазовые переходы второго рода, при которых зависимости μ(P) и μ(T ) изломов не имеют, то есть произ-

водные (20.1) являются непрерывными функциями температуры и давления. Для фазовых переходов второго рода характерны разрывы вторых производных химического потенциала по давлению и температуре в точках фазового перехода. Скачком здесь изменяются следующие величины

∂2μ				∂Vɶ
			=
∂P	2
		T		∂P T

− так называемый удельный коэффициент сжимаемости вещества,

∂2μ				∂Sɶ		Cɶp
			= −		= −
∂T	2					T
		P		∂T P

− удельная теплоемкость при постоянном давлении,

∂2μ		∂Vɶ
	=
∂P ∂T	=
∂P ∂T		∂T P

(20.2)

(20.3)

(20.4)

− удельный коэффициент объемного расширения.

Фазовые переходы второго рода обычно связаны со скачкообразным изменением свойств симметрии тела. Пусть, например, твердое тело обладает кубической симметрией, причем в центре элементарной ячейки кристалла находится некоторый ион.

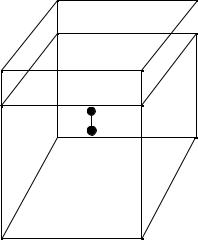
Если при повышении температуры энергетически более выгодным окажется расположении этого иона не в центре ячейки, то кристалл из кубического состояния перейдет в одноосное состояние (решетка деформируется, Рис. 20.1). Такая деформация соответствует фазовому переходу

Рис. 20.1

второго рода. Другие примеры фазовых переходов второго рода будут рассмотрены ниже.

Для фазовых переходов второго рода характерно скачкообразное изменение свойств симметрии тела, связанное с малым перемещением составляющих тело атомов. Такое перемещение происходит без затрат энергии и без изменения объема. В то же время фазовые переходы первого рода требуют подвода в системе тепла и сопровождаются скачкообразным изменением объема. В этом состоит принципиальное отличие фазовых переходов первого и второго рода.

Получим для фазовых переходов второго рода дифференциальные соотношения, заменяющие уравнение Клапейрона-Клаузиса (18.4). В рассматриваемом случае в правой части уравнения (18.4) числитель и знаменатель обращаются в нуль, то есть, возникает неопределенность типа 0 / 0 .

Чтобы обойти эту трудность, разложим каждую из функций

μ1,2 (P,T )

в ряд Тейлора в окрестности некоторой точки плоскости (P,T ) ,

ограничиваясь величинами второго порядка малости. Имеем

μi (P + dP,T + dT ) = μ i

∂μ

dT +

(P,T ) +

dP +

∂P T

∂T P

(20.5)

∂

μi

∂

μ2i dP2

μ2i dT 2

dP dT ,

∂P

∂T

∂P ∂T

где i = 1,2

- номер фазы,

dT и dP − приращения температуры и давления.

Обозначим скачок любого термодинамического параметра A при переходе от одной фазы к другой через [ A], то есть [ A] = A2 − A1 , где A1 и A2 отно-

сятся к первой и второй фазам, соответственно. Тогда вычитая друг из друга выражения (20.5), относящиеся к номерам i = 2 и i = 1, найдем

[μ] = μ

(P,T ) − μ (P,T ) +

∂μ

dP +

∂μ

dT +

∂P T

∂T P

∂

(20.6)

dP2 +

∂

dT 2 +

dP dT .

∂P

∂T

∂P ∂T

Пусть точка (P,T ) принадлежит кривой фазового равновесия (Рис. 17.1). Тогда, поскольку рассматриваются фазовые переходы второго рода,

μ2 (P,T ) − μ1 (P,T ) = 0 ,	∂μ	= [Vɶ] = 0 ,	∂μ	= −[Sɶ] = 0 .
μ2 (P,T ) − μ1 (P,T ) = 0 ,		= [Vɶ] = 0 ,		= −[Sɶ] = 0 .
	∂P T		∂T P

Поэтому вместо (20.6) получаем

	1	ɶ
[μ] =	1	∂V	dP2
[μ] =		∂V	dP2
2		∂P
			T

	1	ɶ		2
−		Cp	(dT )
	2	T

	ɶ		(20.7)
+	∂V	dP dT .	(20.7)
	∂T
		P

При записи (20.7) учтены выражения (20.2)-(20.4). Мы интересуемся дифференциальным уравнением кривой фазового перехода μ 1(P,T ) = μ 2(P,T ) .

Это означает, что дифференциалы dP и dT в (20.7) должны выбираться таким образом, чтобы скачок химического потенциала [μ] ≡ 0 . Следовательно, кривая фазового перехода описывается дифференциальным уравнением

∂Vɶ

[Cɶ

]

dP2

dP dT −

dT 2

= 0 .

(20.8)

∂P

∂T

Выражение (20.8) представляет собой квадратное уравнение для

производной dP . Но природа однозначна, поэтому данное уравнение dT

должно иметь единственное решение. Чтобы это было так, дискриминант квадратного уравнения (20.8) для отношения dP должен быть равен нулю.

						dT
Иными словами,
		ɶ			ɶ		2
[CɶP	]	∂V		+ T	∂V		= 0 .	(20.9)
[CɶP	]			+ T	∂T		= 0 .	(20.9)
		∂P			∂T
			T			P

Тогда для производной dP вдоль кривой фазового перехода из (20.8) по- dT

лучаем

dP		ɶ		ɶ
dP	= −	∂V		∂V	.	(20.10)
	= −	∂T		∂V	.	(20.10)
dT		∂T		∂P
			P		T

В правой части (20.10) стоит отношение скачков удельных коэффициентов объемного расширения и сжимаемости для двух фаз, причем эти скачки

должны быть связаны со скачком теплоемкости CɶP соотношением (20.9).

Выражения (20.9) и (20.10) называются уравнениями Эренфеста для фазовых переходов второго рода. Эти выражения заменяют одно дифференциальное уравнение Клапейрона-Клаузиуса (18.4).

В следующих параграфах мы применим уравнения Эренфеста к анализу фазовых переходов магнетиков и проводников.

§ 21. Ферромагнетизм. Температура Кюри

Рассматривая в §13 термодинамику парамагнетиков, мы предполагали, что их внутренняя энергия зависит только от температуры. Там же было отмечено, что это допущение оправдано при условии, что энергия взаимодействия магнитных моментов молекул много меньше энергии теплового движения молекул. Однако существуют вещества, для которых взаимодействием магнитных моментов молекул пренебречь нельзя. Такие вещества называются ферромагнетиками. В ферромагнетиках, благодаря взаимодействию магнитных моментов молекул, возникает спонтанный магнитный момент и при отсутствии внешнего магнитного поля, то есть

M ¹ 0 при H = 0 .

(21.1)

Для парамагнетиков же, как было отмечено в §13, магнитный момент M = 0 при H = 0 (здесь и далее рассматриваются изотропные среды, на этом основании под M и H понимаются модули соответствующих векторов).

Свойство (21.1) указывает на то, что в веществе присутствует некоторое внутренне магнитное поле, которое отлично от нуля при нулевой напряженности внешнего магнитного поля. Это внутреннее поле ориентирует магнитные моменты молекул даже при отсутствии внешнего поля.

Французский физик П. Вейсс в 1907 году предположил, что внутреннее магнитное поле Hin создается молекулами ферромагнетика, и что

для этого поля верна формула

Hin = γ M .	(21.2)
Под M в (21.2) понимается магнитный момент моля вещества,	γ - некото-

рый коэффициент, который называется коэффициентом Вейсса.

Еще Вейсс допустил, что уравнение состояния парамагнетиков и ферромагнетиков описывается единой формулой

M = M 0 L ( M 0 H /(RT )) ,

(21.3)

но теперь под напряженностью магнитного поля H в (21.3) следует понимать не напряженность внешнего поля H , а сумму этого поля и внутреннего поля (21.2). Тогда (21.3) конкретизируется в виде

M = M 0 L[M 0 (H + γ M ) /(RT )] .	(21.4)
Попытаемся найти из (21.4) магнитный момент моля вещества M .
Как уже отмечалось в §13, функция Ланжевена L(x)	является трансцен-

дентной. Поэтому аналитически решить уравнение (21.4) невозможно. Прибегнем к его графическому анализу.

Обозначим весь аргумент функции Ланжевена через x :

M 0 (H + γ M ) /(RT ) = x ,

(21.5)

что эквивалентно записи

x −

= L(x) ,

γ M 2

γ M

или трансцендентному уравнению относительно x

−

= L(x) .

(21.6)

γ M 2

γ M

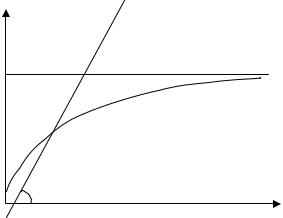
Построим качественно графики левой и правой частей уравнения (21.6). Они представлены на Рис. 21.1, где

f, L

	0	ϕ							x


−	H

	γ M 0	Рис. 21.1
	γ M 0

		f (x) = x	RT		−	H		.	(21.7)
		f (x) = x	γ M	2	−	γ M	0	.	(21.7)
			γ M	2		γ M
			0
Точка пересечения графиков f (x)				и L(x)			на Рис. 21.1 дает числен-

ное значение x , зная которое можно вычислить магнитный момент M по формуле (21.5). Конечно, эта точка пересечения будет зависеть и от магнитного поля и от температуры, так как ими определяется график линейной функции f (x) . В частности, прямая f (x) пересекает ось ординат в

точке −H /(γ M 0 ) и составляет с осью 0x угол ϕ , тангенс которого согласно (21.7) равен

tgϕ = RT /(γ M 2 ) .	(21.8)
0

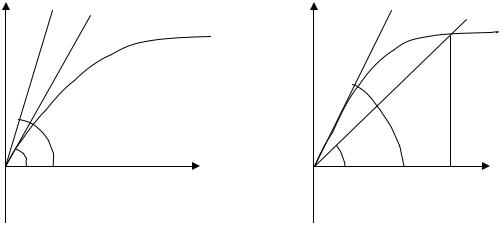
Исследуем магнитный момент вещества при стремлении напряженности внешнего магнитного поля к нулю. Здесь принципиально различаются две ситуации – когда угол ϕ больше, либо меньше угла ψ касательной к кривой Ланжевена в начале координат. Графики для обоих этих случаев представлены на Рис. 21.2 и 21.3.

L, f

ψ ϕ

Рис. 21.2

Рис. 21.3

Рис. 21.2 относится к случаю

′

а Рис. 21.3 –

к случаю

γ M 2

L (0) ,

′

γ M 2

< L (0) .

Введем в рассмотрение величину

g M 02

L¢(x)

(21.9)

которая имеет размерность температуры и называется температурой Кюри. В случае T > Tc (Рис. 21.2) точка пересечения кривых L и f стре-

мится к началу координат при H → 0 . Тогда из (21.5) заключаем, что M → 0 при H → 0 . Этот предел характерен для парамагнетика. В то же время при T < Tc (Рис. 21.3) точка пересечения кривых L и f в пределе

при H → 0 имеет координату x = x0 ¹ 0 . Согласно (21.5), это означает, что

lim M =	R T x0	¹ 0 .	(21.10)

H →0	g M 0
	67

Условие (21.10) соответствует ферромагнитному состоянию вещества. Таким образом, температура Кюри представляет собой температуру

фазового перехода вещества из парамагнитного в ферромагнитное состояние. Микроскопически этот переход трактуют следующим образом. При температуре Кюри тепловое движение молекул становится настолько интенсивным, что разрушает ориентирующее поле Вейсса. При этом наблюдается переход вещества из ферромагнитного в парамагнитное состояние.

Мы рассмотрели феноменологическое микроскопическое описание парамагнитного и ферромагнитного состояний вещества. Обратимся теперь к термодинамике. Покажем, что переход между этими состояниями является фазовым переходом второго рода. Соответствующая теория была развита Л.Д. Ландау.

В парамагнетиках, согласно §13, вклад во внутреннюю энергию дают напряженность магнитного поля и магнитный момент. Но в §13 анализировались вещества при постоянном объеме и давлении. Сейчас рассмотрим более общий случай, когда давление и объем могут изменяться. Это случай поливариантной системы, в которой обобщенными координатами являются объем V и магнитный момент M , а обобщенными силами, сопряженными этим координатам – давление P и напряженность магнитного поля H . Согласно §2, данная система имеет три степени свободы. Получим выражения для ее потенциала Гиббса.

Основное равенство термодинамики для вещества в магнитном поле в случае фиксированного числа частиц в системе, в соответствии с (10.12) и (13.8), имеет вид

dE = T dS − P dV + H dM .

Тогда для системы с переменным числом частиц N по аналогии с (15.2) будем иметь

dE = T dS − P dV + H dM + μ dN .

(21.11)

Рассчитаем удельную энергию Eɶ, приходящуюся на одну молекулу. Для рассматриваемой поливариантной системы это функция трех интенсивных

параметров. Выберем в качестве таковых удельные величины Sɶ, Vɶ , Mɶ , т. е. положим Eɶ = Eɶ(Sɶ,Vɶ, Mɶ ) . В соответствии с определением удельной энер-

гии

	ɶ	ɶ		ɶ
dE = d (N Eɶ) = EɶdN + N dEɶ = EɶdN + N	∂E dSɶ +	∂E	dVɶ +	∂E
				∂Mɶ
	∂Sɶ	∂Vɶ

Воспользовавшись в (21.12) очевидными равенствами

dMɶ . (21.12)

N dSɶ = dS − SɶdN , N dVɶ = dV − VɶdN , N dMɶ = dM − Mɶ dN

и сгруппировав члены, находим

	ɶ	ɶ		ɶ		ɶ	ɶ		ɶ
dE = Eɶ	− Sɶ ∂E − Vɶ	∂E	− Mɶ	∂E	dN +	∂E dS +	∂E	dV +	∂E	dM .	(21.13)
		∂Vɶ		∂Mɶ
	∂Sɶ					∂Sɶ	∂Vɶ		∂Mɶ
						68

Сравнивая (21.13) и (21.11), заключаем, что

T =

∂Eɶ

P = −

∂Eɶ

H =

∂Eɶ

(21.14)

∂Sɶ

∂Vɶ

∂Mɶ

ɶ ɶ

V ,M

S ,M

S ,V

∂Eɶ

μ = Eɶ − Sɶ ∂Sɶ

− Vɶ

− Mɶ

= Eɶ

− T Sɶ + PVɶ − Mɶ H .

∂Vɶ

∂Mɶ

Таким образом, вместо химического потенциала моновариантной системы (15.8) мы теперь имеем потенциал

′	ɶ	(21.15)
μ = μ − M H ,
где
μ′(Sɶ,Vɶ, Mɶ ) = Eɶ − T Sɶ + PVɶ.		(21.16)

По аналогии с моновариантной системой определим термодинамический потенциал Гиббса соотношением

Φ = N μ = E − T S + PV − MH .

(21.17)

При фиксированных значениях T , P , H потенциал (21.17) достигает минимума в состоянии равновесия. Докажем это. В согласии с определением (21.17), имеем

dΦ = dE − T dS − S dT + P dV + V dP − H dM − M dH .	(21.18)
Здесь по первому началу термодинамики
dE = δQ − P dV + H dM ,	(21.19)
где H dM - работа намагничения, найденная в §13. Но согласно §16,
δQ ≤ T dS ,	(21.20)

где знак равенства относится к равновесным процессам. Подставляя

(21.19) в (21.18) и учитывая (21.20), находим

dΦ ≤ V dP − S dT − M dH .

Таким образом, в случае протекания любого процесса при постоянных значениях P , T и H имеет место неравенство

dΦ ≤ 0 ,

где знак равенства соответствует состоянию равновесия. Это, очевидно, означает, что в состоянии равновесия потенциал Φ минимален. Отсюда и из определения (21.17) следует также, что при фиксированном числе молекул N , в равновесии достигает своего минимума и химический потенциал

μ вида (21.15).

Исследуем условия минимума потенциала μ . Для этого перейдем от

переменных Sɶ, Vɶ , Mɶ к переменным T , P , Mɶ . Возможность такого перехода очевидна из выражений (21.14), записанных в виде

T =	∂Eɶ(Sɶ,Vɶ, Mɶ )	= T (Sɶ,Vɶ, Mɶ	) ,	P = −	∂Eɶ(Sɶ,Vɶ, Mɶ )	= P(Sɶ,Vɶ, Mɶ	) .	(21.21)

	∂Sɶ				∂Vɶ

Уравнения (21.21) принципиально могут быть решены относительно Sɶ и Vɶ . Тогда μ′ в выражении (21.16) будет функцией

′ ′	ɶ	(21.22)
μ = μ	(T , P, M ) .	(21.22)

Основное допущение Ландау состоит в том, что функции (21.15) и (21.22) определены как для равновесных, так и для неравновесных состояний. При этом выход магнитного вещества из состояния равновесия при заданных значениях T , P и H обеспечивается отклонением магнитного

момента Mɶ от его равновесного значения. Ландау исследовал вещества вблизи условий равновесия ферромагнитной и парамагнитной фаз, когда

магнитный момент Mɶ стремится к нулю. На этом основании он предположил, что функция (21.22) допускает разложение в ряд Тейлора по степе-

ням Mɶ . Далее будут рассматриваться изотропные среды. Свойства таких сред не зависят от знака Mɶ . Это означает, что их термодинамические параметры являются функциями квадрата Mɶ 2 , так что в названный ряд будут

входить только целые степени величины Mɶ 2 .

Математически допущения Ландау записываются в форме

′	+	α(T , P) ɶ	2	+	β(T , P) ɶ 4	ɶ	(21.23)
μ = μ (T , P,0)	+	M		+	M	− M H ,	(21.23)
		2			4

где α(T , P) и β(T , P) − некоторые коэффициенты. При получении (21.23)

мы ограничились в ряде Тейлора для функции (21.22) тремя главными членами. Мы считаем, что выражение (21.23) справедливо как для равновесных, так и неравновесных состояний, при этом данные состояния отли-

чаются друг от друга только значениями магнитного момента Mɶ при одинаковых давлении, температуре и магнитном поле.

Как установлено выше, в состоянии равновесия при условиях

T = const , P = const , H = const

химический потенциал (21.23) должен достигать минимума. Необходимое

и достаточное условия минимума μ относительно переменной Mɶ								таковы:
	∂μ
			= Mɶ[α(T , P) + β(T , P) Mɶ 2 ] − H = 0 ,					(21.24)
	∂Mɶ		= Mɶ[α(T , P) + β(T , P) Mɶ 2 ] − H = 0 ,					(21.24)
			∂2μ
				= α(T , P) + 3β(T , P) Mɶ 2 > 0 .				(21.25)
		∂Mɶ 2		= α(T , P) + 3β(T , P) Mɶ 2 > 0 .				(21.25)
Рассмотрим предельный случай при H → 0 . В нем уравнение (21.24)
будет иметь два корня:					= 0 ,
				Mɶ	= 0 ,			(21.26)
				Mɶ = MɶS =		− α(T , P)	.	(21.27)
						β(T , P)
При этом неравенство (21.25) дает
				α(T , P) > 0				(21.28)
для корня (21.26). Для корня (21.27) Ландау записал:
			α(T , P) < 0 ,			β(T , P) > 0 .		(21.29)
					70

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.11.2019116.74 Кб2ТЕМАТИКА филологи.doc
#
05.11.2018221.7 Кб25Темы 1-3 по ХП.doc
#
18.04.201588.84 Кб31Темы семинарских занятий 3 этап по ГП.docx
#
18.04.201589.48 Кб11Темы семинарских занятий по ГП (4 этап).docx
#
09.11.201892.67 Кб3Теория государства и права.doc
#
18.04.2015836.09 Кб78Термодинамика ч1 - Сотский А.Б..pdf
#
08.05.201972.39 Кб32Термомеханическая обработка стали.docx
#
27.11.201965.02 Кб7Тест 3.Ферменты.Витамины.Гормоны.doc
#
18.04.201554.62 Кб42Тест по курсу Правотворческий процесс.docx
#
18.04.201554.78 Кб177Тестирование по теме Правотворчество.doc
#
18.04.2015208.38 Кб246Тестовые задания с ответами физика лазеров.doc