
Векторная алгебра и аналитическая геометрия
.pdf
А проводят вектор AB , равный второму слагаемому, из точки В – вектор BC , равный третьему слагаемому и т.д. Наконец, строят последний вектор с концом в точке D, вектор OD , замыкающий полученную ломаную линию, и будет искомой суммой (рис. 1.16).
Пример 1.12. В пространстве заданы векторы a (1, 2, –2) и b (–3, 5, 1), найдите следующие векторы: а) a +b ; б) a −b ; в) 2a +1 3b.
Решение. При сложении (вычитании) векторов соответствующие их координаты складываются (вычитаются). Таким образом, координаты векторов равны: а) a +b (–2, 7, –1); б) a −b (4, –3, –3); в) 2a +1 3b (1, 17/3, –11/3).
Пример 1.13. Разложите в плоскости вектор a (1; 2) по базису. Решение. В качестве базисных векторов на плоскости рас- 
 сматривают i и j – векторы, по модулю равные единице и на-
сматривают i и j – векторы, по модулю равные единице и на-  правленные по координатным осям Ox и Oy. Тогда видим, что
правленные по координатным осям Ox и Oy. Тогда видим, что 



a =i +2 j (рис. 1. 17). Действительно, ведь координаты вектора 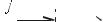
–это и есть коэффициенты в разложении вектора по базису.
Втрехмерном случае рассматриваются базисные векторы
|
|
, |
|
|
, |
k |
. Можно говорить о том, |
что записи |
a |
(x, y, z) |
и |
a |
= xi |
+ y |
j |
+ zk |
рав- |
||||||||||||
|
i |
|
j |
||||||||||||||||||||||||||
нозначны, в дальнейшем будем пользоваться обеими этими записями. |
|||||||||||||||||||||||||||||
|
|
|
|
|
Пример 1.14. Найдите |
α и β, |
если |
|
известно, |
что векторы |
|||||||||||||||||||
|
r |
|
|
r |
|
r |
и b = i +βj +2k |
коллинеарны. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
= αi |
+7 j +3k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Решение. В условии задачи векторы записаны в разложении по базису |
||||||||||||||||||||||||
пространства, в другой записи имеем: |
|
(α, 7, 3), |
|
(1, β, 2). Векторы колли- |
|||||||||||||||||||||||||
a |
b |
||||||||||||||||||||||||||||
неарны, если их координаты пропорциональны, т. е. α |
= 7 |
= 3 |
. Следователь- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
β |
2 |
|
|
|
|
|
|||
но, α = 3/2, β = 14/3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Ответ: α = 3/2, β = 14/3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1.5. Скалярное произведение векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Скалярным произведением векторов |
|
|
и |
|
|
называется число, равное |
||||||||||||||||||
|
|
|
|
|
a |
|
b |
||||||||||||||||||||||
произведению их модулей на косинус угла между ними. Обозначаться скалярное произведение может: a b , a b , или ( a ,b ).
Пример 1.15. Вычислите скалярное произведение векторов ar = −i +7 j +3k и b = i +8 j −2k .
11

Решение. Известно, что скалярное произведение векторов равно сумме произведений их соответствующих координат. Следовательно, a b = (−1) 1+7 8 +3 (−2) = 49.
Ответ: a b = 49 .
Пример 1.16. Найдите косинус угла между векторами a и b , если:
а) a (5, 4, –2), b (–2, 1, 2); б) a (3, –3, –6), b (–1, 1, 2); в) a (1, 2, –1), b (3, 4, 11).
|
|
|
|
Решение. По определению скалярного произведения имеем равенство |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
cos ( |
|
,ˆ |
|
) , значит cos ( |
|
|
|
,ˆ |
|
|
|
|
) = |
|
|
|
a |
b |
|
, т. е. ( |
|
,ˆ |
|
) = arccos |
|
a |
|
b |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
a |
b |
a |
b |
a |
b |
a |
b |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
b |
|
a |
|
b |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 (−2) +4 1+(−2) 2 |
|
||||||||||||||||||||||||||||||||||||||||||
а) Подставим данные: cos ( |
|
,ˆ |
|
) = |
a |
b |
|
= |
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
52 + 42 +(−2)2 (−2)2 +12 +22 |
|||||||||||||||||||||||||||||||
= |
|
−10 |
= − 10 |
= − 2 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
45 |
9 |
|
|
9 |
5 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) |
|
cos (a,ˆb) = |
|
|
|
|
−3 −3 −12 |
= |
|
|
|
−18 |
|
= − |
18 |
|
|
= − 18 |
|
|
= −18 |
= −1. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 +9 +36 1+1+4 |
54 |
6 |
54 6 |
324 |
18 |
|
||||||||||||||||||||||||||||||||||||||||||||
В этом случае косинус угла равен –1, значит, угол между векторами составляет 180° и они противоположно направленные. Действительно, b = –3 a , т. е. векторы коллинеарные, а раз множитель отрицателен, то они противоположно направленные.
в) cos (a,ˆb) = |
3 +8 −11 |
= |
0 |
= 0 . В этом случае косинус |
1+4 +1 9 +16 +121 |
6 146 |
угла равен 0, т. е. угол между векторами составляет 90°, и они ортогональны.
|
Пример |
1.17. |
|
Зная |
векторы, |
образующие |
треугольник ABC: |
||||||||||||||
|
= 2ir |
−6 rj , |
|
|
|
=ir |
+7 rj , |
|
=3i − j , найти углы этого треугольника. |
||||||||||||
AB |
BC |
AC |
|||||||||||||||||||
|
Решение. Для того чтобы найти углы заданного треугольника надо найти |
||||||||||||||||||||
|
|
|
косинусы углов между векторами, образующими треугольник. |
||||||||||||||||||
|
|
|
Это можно сделать, используя определение скалярного произ- |
||||||||||||||||||
|
|
|
ведения. Но косинус угла определен для векторов, имеющих |
||||||||||||||||||
|
|
|
общее начало. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Угол А треугольника ABC равен углу между векторами |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
AB и AC . Можем найти его косинус: |
cos ( AB,ˆAC) = |
||||||||||||||||
|
|
|
|
cos A = |
|||||||||||||||||
|
|
|
|
|
|
|
|
6 +6 |
|
|
|
12 |
6 |
|
ˆ |
||||||
|
|
= |
|
|
4 +36 9 +1 |
= |
40 |
10 =10 = 0,6 . Значит, |
A = arccos 0,6 . |
||||||||||||
12

Чтобы найти косинус угла В треугольника ABC надо искать косинус угла между векторами BA и BC (рис. 1.18). Зная что BA = −AB , BA (–2, 6), имеем
|
|
ˆ |
|
|
|
|
|
|
|
|
|
BA |
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
−2 +42 |
|
40 |
|
|
|
4 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
cos B = cos (BA,ˆBC) = |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
4 +36 |
1+49 |
= |
|
40 |
50 = |
|
|
5 . Значит, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
BA |
BC |
|||||||||||||||||||||||||||||||||||||||||||||
|
ˆ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
B = arccos |
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Косинус угла С треугольника ABC есть косинус угла между векторами |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
и |
|
(рис. 1.18), где |
|
|
|
|
= − |
|
|
|
|
|
|
и |
|
(–3, 1), |
а |
|
= − |
|
, |
|
|
(–1, –7). |
||||||||||||||||||||||
CA |
CB |
CA |
AC |
CA |
CB |
BC |
CB |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 −7 |
|
|
|
|
−4 |
|
|
|
2 |
|||||||||
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
CB |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Итак, cos C = cos (CA,ˆCB) = |
|
|
|
|
|
|
|
|
|
|
|
= |
|
9 +1 |
1+49 = |
10 50 = − 5 |
5 . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
CA |
CB |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, C = arccos (−5 |
5 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
ˆ |
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
Ответ: A = arccos 0,6 , B = arccos |
|
5 , C = arccos (− 5 ) . |
ar = i +2 j +k |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
Пример 1.18. |
При каком |
значении α |
векторы |
и |
||||||||||||||||||||||||||||||||||||||||||
br = 2ir +αrj +2kr ортогональны?
Решение. Два вектора ортогональны друг другу, если угол между ними составляет 90°. Следовательно, косинус угла между ними должен быть равен нулю и, если сами векторы не нулевые, то скалярное произведение равно нулю. Запишем на математическом языке условие ортогональности (перпендикулярности) двух векторов: a b a b = 0 . Подставим данные: a b
a b =1 2 +2 α+1 2 = 0 . Из уравнения 2+2α+2=0 имеем: α = −2 .
Ответ: α = −2 .
Пример 1.19. В плоскости XOZ найти вектор a , перпендикулярный век- r(6,−3, 2) и имеющий одинаковую с ним длину.
Решение. Пусть вектор a имеет координаты (x, y, z). В плоскости XOZ лежат все такие точки и векторы, у которых вторая координата равна нулю.
Т. е. a (x, y, z) XOZ y = 0.
Из того, что a c следует a c = 0 . Можем теперь составить уравнение x 6 + y (−3) + z 2 = 0 , зная, что y =0 , получим 6x +2z = 0.
По условию длины векторов a и c равны, т. е. a =  x2 + y2 + z2 =
x2 + y2 + z2 =
=  36 +9 +4 = c .
36 +9 +4 = c .
13
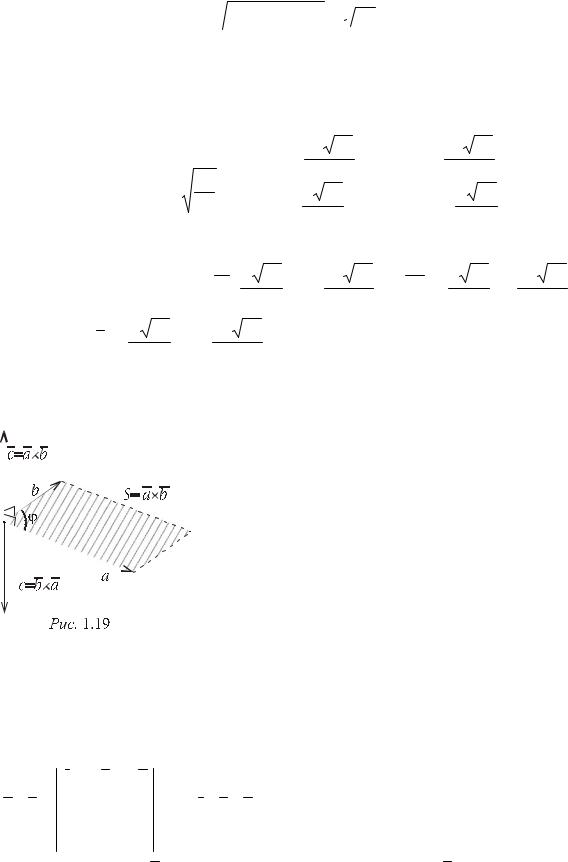
Составим уравнение 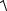 x2 + y2 + z2 =
x2 + y2 + z2 =  49 , из которого, зная что y =0 ,
49 , из которого, зная что y =0 ,
получим x2 + z2 = 49 .
Решим полученные уравнения вместе: |
6x +2z =0, |
|
|
2 |
z = −3x, |
|
||||||
|
2 |
+ z |
2 |
= 49, |
|
+(−3x) |
2 |
= 49, |
||||
|
x |
|
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
z = −3x, |
|
|
|
|
21 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 10 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
z = −3x, |
|
|
|
z = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
z |
= |
|
|
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
49 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
10x2 = 49, |
x = ± |
10 |
|
|
|
7 10 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
7 |
10 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
10 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Видим, что условию удовлетворяют два вектора, являющиеся противо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
положно направленными: a |
|
(7 |
10 , 0, − 21 |
|
|
|
|
10 ) и a |
2 |
(−7 |
10 , 0, 21 10 ) . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
10 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
Ответ: a (± 7 |
10 , 0, m 21 10 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
10 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1.6. Векторное произведение векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторным произведением векторов |
|
|
|
и |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
называется третий вектор |
|
|
(рис. 1.19), если вер- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ны следующие условия: |
|
,ˆ |
|
|
) ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
a |
|
|
b |
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
и |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
a |
c |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
, |
|
|
|
, |
|
|
|
|
|
образуют правую тройку. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
c |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначается векторное произведение: |
|
× |
|
. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторное произведение векторов не ком- |
|||||||||||||||||||||||||||||||||||||||||||||||
мутативно, т. е. нельзя переставлять сомножители векторного произведения. Пример 1.20. Вычислите векторное произведение векторов
ar = −i +7 j +3k и b = i +8 j −2k .
Решение. Векторное произведение векторов вычисляется по формуле:
i j k
a ×b = xa ya za , где i , j , k – базисные вектора (орты), (xa , ya , za ) – ко- xb yb zb
ординаты вектора a , (xb , yb , zb ) – координаты вектора b .
14

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
В задаче |
|
|
(–1, 7, 3), |
|
|
(1, 8, –2), значит |
|
× |
|
|
= |
−1 |
7 |
|
3 |
. Вычислим |
|||||||||||||||||||||||||||||
a |
b |
a |
b |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
8 |
−2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
i |
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
определитель: |
−1 |
7 |
|
3 |
= −14 |
|
−8 |
|
+3 |
|
−(7 |
|
+ 24 |
|
+ 2 |
|
) = −38 |
|
+ |
|
−15 |
|
. |
||||||||||||||||||||||
|
i |
k |
j |
k |
i |
j |
i |
j |
k |
||||||||||||||||||||||||||||||||||||
|
1 |
8 |
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, a ×b = −38i + j −15k .
Ответ: |
|
× |
|
(–38, 1, –15). |
|
|
||||
a |
b |
|
|
|||||||
Пример 1.21. Найдите площадь параллелограмма, построенного на век- |
||||||||||
r |
r |
|
|
r |
|
r |
r |
r |
r |
−k , как на сторонах. |
торах a |
= i |
−1 j |
+2k |
и b |
= 2i |
−3 j |
||||
Решение. Модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах, как на сторонах. Действительно, a ×b = a b sin(a,ˆb) , а правая часть этого равенства есть
формула площади параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.19). Следовательно, искомая площадь S = a ×b .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
|
k |
|
|
|
|
|
||
|
|
В задаче |
|
|
|
|
(1, –1, 2), |
|
|
(2, –3, –1), значит |
|
× |
|
|
= |
1 |
−1 |
|
|
2 |
. Вычислим |
||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
−3 |
−1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
j |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
определитель: |
|
1 |
|
−1 |
2 |
|
|
= |
|
|
|
−3 |
|
|
|
+4 |
|
−(−2 |
|
−6 |
|
− |
|
) = 7 |
|
+5 |
|
− |
|
. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
i |
k |
j |
k |
i |
j |
i |
j |
k |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
−3 |
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Таким образом, |
|
|
× |
|
= 7 |
|
+5 |
|
− |
|
. Найдем модуль полученного векторно- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
i |
j |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
го произведения: |
|
× |
|
|
|
= |
72 +52 +(−1)2 |
= 75 . Т. е. площадь параллело- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
грамма равна |
75 |
масштабных единиц в квадрате. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ответ: S = |
|
|
|
75 кв. ед. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Пример |
1.22. |
|
|
|
|
|
Зная векторы, |
образующие |
|
треугольник |
ABC: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= ir −3rj + |
|
, |
|
= ir +5 j − |
|
, |
|
= 2i +2 j , найти |
длину высоты |
этого |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AB |
k |
BC |
k |
AC |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
треугольника, опущенной из точки В.
Решение. Для нахождения длины высоты воспользуемся формулами площади треугольника. С одной стороны площадь треугольника равна поло-
вине произведения основания на высоту S = 12 AC BH (рис. 1.20), а с дру-
15
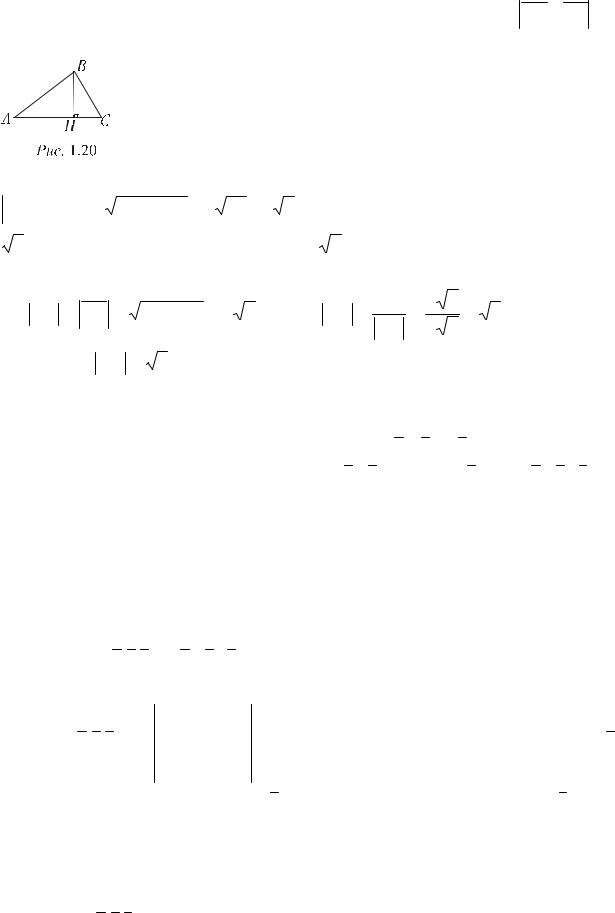
гой – половине площади параллелограмма, построенного на векторах, как на сторонах, т. е. половине модуля векторного произведения S = 12 AC × AB .
|
|
|
|
|
|
i |
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
|
Вычислим |
|
× |
|
= |
2 |
2 |
0 |
= 2 |
|
−6 |
|
−(−2 |
|
+2 |
|
) = |
||||||
AC |
AB |
i |
k |
k |
j |
|||||||||||||||||
|
1 |
−3 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
−2 |
|
−4 |
|
. |
|||||
i |
j |
k |
||||||||||
|
|
|
|
|
|
|
|
Найдем модуль полученного векторного произведения: |
||||
|
× |
|
|
|
= = 4 +4 |
+16 = 24 = 2 6 . Т. е. площадь треугольника ABC равна |
||||||
AC |
AB |
|
||||||||||
6 масштабных единиц в квадрате, S = |
6 . |
|
|
|
|
|
|
|
Найдем длину стороны АС, она равна модулю соответствующего векто- |
||||||||
ра: AC = AC = |
4 +4 +0 = 2 2 . Тогда |
BH = |
2S |
= |
2 |
6 |
= |
3 (ед.) |
|
|
|
AC |
|
2 |
2 |
|
|
Ответ: BH = |
3 . |
|
|
|
|
|
|
|
1.7. Смешанное произведение векторов
Смешанным произведением трех векторов a , b и c называется число, равное скалярному произведению вектора a ×b на вектор c , т. е. ( a ×b , c ).
Обозначаться смешанное произведение может: |
|
|
|
|
|
|
или |
|
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
a |
b |
a |
b |
c |
|
||||||||||||||||||||||
|
|
c |
|
||||||||||||||||||||||||
Пример |
1.23. Вычислите смешанное произведение |
векторов |
|||||||||||||||||||||||||
ar = −i +7 j +3k , b = i +8 j −2k и |
|
= i + j −k . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
c |
|
r |
|
|
|
r |
|
|
|||||||||||||||||||
Решение. |
Векторное произведение |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
+3k |
и |
||||||||
векторов a |
= −i |
+7 j |
|||||||||||||||||||||||||
br = ir +8 rj −2kr |
вычислено в примере 1.20: |
|
× |
|
= −38 |
|
+ |
|
−15 |
|
. Значит, |
по |
|||||||||||||||
a |
b |
i |
j |
k |
|||||||||||||||||||||||
определению a b c = ( a ×b , c ) = (–38, 1, –15) (1, 1, –1) = –38 + 1 + 15 = – 22.
Можно воспользоваться формулой для вычисления смешанного произ- xa ya za
ведения a b c = xb yb zb , где (xa , ya , za ) – координаты вектора a , xc yc zc
(xb , yb , zb ) – координаты вектора b , (xc , yc , zc ) – координаты вектора c .
|
|
|
|
|
= |
|
−1 |
7 |
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
8 |
−2 |
= 8 + 3 – 14 – 24 – 2 + 7 = –22. |
|
a |
|
b |
c |
|||||||
|
|
1 |
1 |
−1 |
|
|||||
Ответ: a b c = –22.
16

Пример 1.24. Компланарны ли три векторы ar = −i − j +3k , br = −3ir +2 rj −2k и c =3ir +3rj −9k ?
Решение. Векторы называются компланарными, если они лежат в одной плоскости. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
|
|
|
Вычислим |
смешанное произведение данных трех векторов: |
a |
|
b |
|
c |
= |
|||
= |
|
−1 |
−1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
−3 |
2 |
−2 |
|
|
= 18 – 27 + 6 – 18 – 6 + 27 = 0. Значит, данные векторы ком- |
|||||||
|
|
3 |
3 |
−9 |
|
|
|
|
|
|
|
|
|
планарны, т. е. лежат в одной плоскости.
Пример 1.24. Найти объем V пирамиды ABCD, построенной на векторах
AB = ir −3rj +k , AC = ir +2 j −k , AD = −2i −5 j .
Решение. Модуль смешанного произведения трех векторов, выходящих из одной точки, равен объему параллелепипеда, построенного на этих векторах. Следовательно, объем треугольной пирамиды – это шестая часть модуля смешанного произведения векторов, на
которых она построена, т. е. V = |
1 |
|
|
|
|
|
|
|
. |
|||||||||||||||
AB |
AC |
AD |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим |
смешанное |
произведение трех данных векторов: |
|||||||||||||||||||
|
|
1 |
−3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
= |
|
1 |
2 |
−1 |
|
|
|
= 0 – 5 – 6 + 4 – 5 – 0 = – 12. |
||||||||||
|
AB |
AC |
AD |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
−2 |
−5 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, V = |
1 |
|
−12 |
|
= |
1 12 = 2 (куб. ед.) |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: V = 2.
2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2.1. Прямая на плоскости
Общее уравнение прямой на плоскости имеет вид: Ax + By +C = 0 . Иногда в общем уравнении выражают y через x и получают уравнение прямой с угловым коэффициентом: y = kx +b .
Пример 2.1. Построить прямые на плоскости, заданные общими уравне-
ниями: а)l1 : 2x + y −3 = 0 ; б)l2 : x +5 = 0 ; в)l3 : 2 y −4 = 0 ; г)l4 : 3x −2 y = 0 .
17

Решение:
а) Прямая l1 задана уравнением 2x + y −3 = 0 . Если x = 0 , то 2 0+y–3=0 и y=3, и точка A(0;3) принадлежит прямой l1, что записывается: A(0;3) l1.
Пусть x =1, тогда 2 1+y–3=0 и y=1, то есть B(1;1) l1. Известно, что две точки однозначно определяют прямую на плоскости (рис. 2.1).
б) Прямая l2 задана уравнением x +5 = 0 , это значит, что абсцисса любой точки этой прямой равна –5, а ордината произвольная. Например, точки A(−5;0) и B(−5;2) определяют прямую l2 (рис. 2.2). Если в общем уравнении коэффициент при y равен нулю, то прямая параллельна оси Oy.
в) Из уравнения 2 y −4 = 0 следует, что произвольная точка прямой l3 имеет ординатой y = 4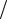 2 = 2 , а абсциссой любое число. Например, точки A(−1;2) и B(3;2) определяют прямую l3 (рис. 2.3). Если в общем уравнении
2 = 2 , а абсциссой любое число. Например, точки A(−1;2) и B(3;2) определяют прямую l3 (рис. 2.3). Если в общем уравнении
коэффициент при x равен нулю, то прямая параллельна оси Ox. |
|
||||||
г) Подставим в уравнение l4 : 3x −2 y = 0 значения x и, вычислив y, |
составим |
||||||
таблицу значений координат точек: |
x |
|
0 |
|
2 . Таким образом, точки |
O(0;0) и |
|
|
|
||||||
y |
|||||||
|
0 |
|
3 |
|
|||
|
|
|
|
|
|
|
|
A(2;3) определяют l4 (рис. 2.4). Если в общем уравнении прямой свободный коэффициент равен нулю, то прямая проходит через начало координат.
Пример 2.2. Найти общее уравнение прямой на плоскости, если известно, что она проходит через точку (2;–1) и составляет с осью Ox угол в 30°.
Решение. Рассмотрим в общем виде уравнение прямой, проходящей через данную точку (x0 ; y0 ) в заданном направлении: y − y0 = k(x − x0 ) . В 
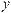 этом уравнении коэффициент k – это характеристика направления прямой, k = tgα, где α – угол наклона
этом уравнении коэффициент k – это характеристика направления прямой, k = tgα, где α – угол наклона
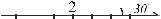 прямой к оси Ox.
прямой к оси Ox.
В задаче k = tg30o = 13 , координаты известной точки равны (2;–1) (рис. 2.5). Можем составить урав-
18
нение: y −(−1) = |
1 |
(x −2) , раскроем скобки и перенесем все слагаемые вле- |
||||
|
|
|
3 |
|
|
|
во: |
1 |
x + y +1+ |
2 |
= 0 или x + 3y + 3 +2 = 0 , это и есть искомое общее |
||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
||
уравнение прямой.
Пример 2.3. Найти угол между прямыми l1 и l2 , заданными уравнения-
ми: а) l1 : x + y +1 = 0 , l2 : 2x − y +3 = 0 ; б) l1 : 6x −2 y +1 = 0 , l2 : 3x − y −8 = 0 ;
в) l |
: 2x − y +3 |
= 0 , l |
2 |
: |
1 x + y −1 = 0 . |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
k1 −k2 |
|
|
|
Решение. |
Известно, что tg (l1,l2) = |
|
|
|
, |
||||
|
1 |
+ k1 k |
2 |
|||||||
|
|
|
|
|
|
|
||||
где k1, k2 – угловые коэффициенты l1 и l2 соответст- |
|||
венно. |
|
|
|
а) |
Прямые l1 и l2 заданы общими уравнениями |
||
(рис. 2.6), выразим y через x, узнаем угловые коэффици- |
|||
енты: |
x + y +1 = 0 y = −x −1, |
т. е. |
k1 = −1; |
2x − y +3 = 0 y = 2x +3, |
т. е. k2 = 2 . Подставим полу- |
|||||
|
|
−1−2 |
|
−3 |
|
|
ченные коэффициенты: |
tg (l1,l2 ) = |
= |
= 3 , |
|||
1+(−1) 2 |
−1 |
|||||
значит, искомый угол (l1,l2 ) = arctg3 .
б) Перепишем данные общие уравнения через угло-
вые коэффициенты: l1 : 6x −2 y +1 = 0 y = 3x + 12 , k1 =3; l2 : 3x − y −8 = 0 y = 3x −8, k2 = 3. Подставим коэффи-
циенты: tg (l1,l2 ) = 13+−332 = 100 = 0 , значит, искомый угол
(l1,l2 ) = arctg0 = 0o (рис. 2.7).
|
Если угловые коэффициенты прямых равны, то |
|||||
такие прямые параллельны. |
|
|
|
|||
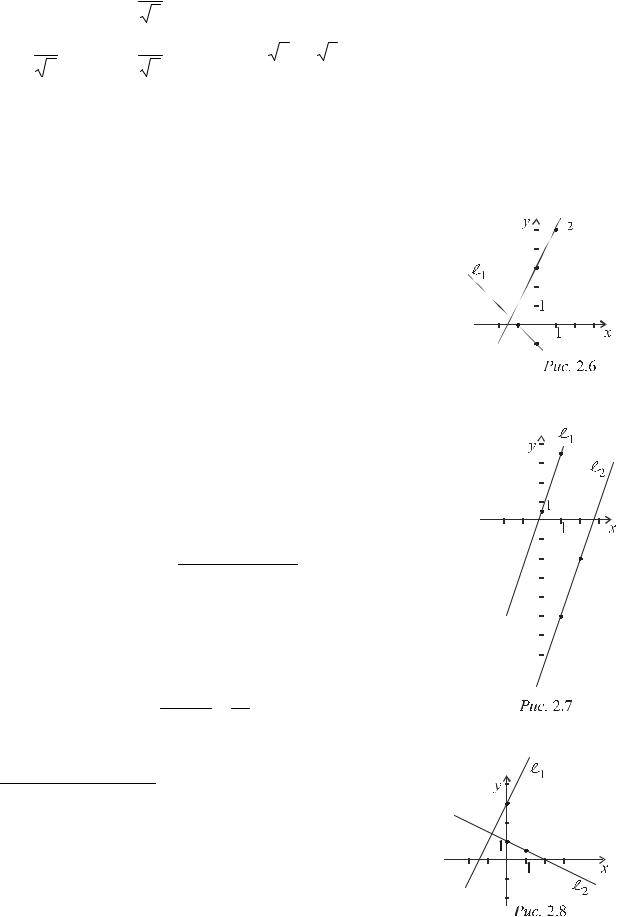
|
в) Уравнения с угловыми коэффициентами для |
|||||
l |
: y = 2x +3 , |
для |
l |
2 |
: y = −1 x +1. |
Тогда |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
19
|
2 −(−1 2) |
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
tg (l1,l2 ) = |
|
|
= |
|
не |
существует, |
следовательно, |
|
(l1,l2 ) = 90 |
||||||||||||||||||
1+2 (−1 2) |
|
0 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(рис. 2.8). Если k = − |
1 |
|
, то прямые перпендикулярны. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2.4. Составить общее уравнение прямой, проходящей через |
|||||||||||||||||||||||||||
точки A(3;−1) и B(−1;2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Решение. Уравнение прямой на плоскости, проходящей через две точки |
|||||||||||||||||||||||||||
|
A(x |
; y |
) и B(x |
2 |
; y |
2 |
) имеет вид: |
x − x1 |
|
= |
|
y − y1 |
. В нашем |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
x2 − x1 |
|
|
y2 − y1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
случае (рис. 2.9) имеем: |
|
x −3 |
= |
|
y −(−1) |
, |
|
x −3 |
= |
|
y +1 |
. Вос- |
||||||||||||||
|
|
|
|
|
|
|
−4 |
|
|
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−1−3 2 −(−1) |
|
|
|
|
|
|
|
|||||||
|
пользуемся |
свойством |
пропорции: (x −3) 3 = ( y +1) (−4) |
||||||||||||||||||||||||
|
3x −9 = −4 y −4 3x +4 y −5 = 0. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пример 2.5. Найти уравнение прямой, отсекающей на оси Oy отрезок длины 3 и образующей с прямой 3x − y +1 = 0 угол в 45o.
Решение. Для того чтобы составить уравнение искомой прямой, надо найти точку, лежащую на ней, и направление, тогда можно будет воспользоваться уравнением y − y0 = k(x − x0 ) .
Искомая прямая образует угол в 45o с прямой y = 3x +1, значит, можно воспользоваться формулой для
нахождения |
угла |
между |
прямыми. |
Получим |
||||
tg45o = |
k −3 |
, т. е. |
k −3 |
=1 k −3 = 3k +1 k = −2 . |
||||
1+3k |
1+3k |
|||||||
|
|
|
|
|
||||
Известно, что искомая прямая отсекает на оси Oy отрезок длины 3, т. е. она проходит (рис. 2.10) либо через точку A1(0;3) , либо через точкуA2 (0;−3) . В первом случае уравнение будет иметь вид y −3 = −2(x −0) , т. е.
y = −2x +3, а во втором y +3 = −2(x −0) , т. е. y = −2x −3.
Ответ: y = −2x ±3.
Пример 2.6. Составить уравнение стороны AB, медианы BM и высоты
CH треугольника ABC, если A(0;−1) , B(3;2) , C(−2;5) .
20
