Теорема 1

независимые переменные, а являются функциями переменных v1, v2,..., vm . В этом случае дифференциалы dxi ≠ xi , а в свою очередь вычисляются по формулам

Доказательство этой теоремы легко провести самостоятельно.

Если u = f (x1, x2 ,..., xi ,..., xn ) и w = g(x1, x2 ,..., xi ,..., xn ) - функции n переменных, то при вычислении дифференциалов справедливы следующие правила:

d(c u)= c du , где c = const ; d(u ± w)= du ± dw ;

d(u w) = u dw + w du ;

d (u )= du w −u dw ;

w w2

5.df fw′ dw .(w)=

Эти правила удобно использовать при вычислении дифференциалов сложных функций.

Пример 2

Найти дифференциал функции трех переменных w = 3xyz .

Решение

dw = (3xyz )′xyz d(xyz)= 3xyz ln 3 (yz dx + xz dy + xy dz).

3.2. Геометрический смысл дифференциала функции двух переменных. Уравнение касательной плоскости и нормали к поверхности.

Теорема

Если функция z = f (x, y) - дифференцируема в точке (x0 , y0 ), то существует не параллельная оси Oz касательная плоскость к поверхности z = f (x, y) в точке M 0 (x0 , y0 , f (x0 , y0 )), уравнение которой имеет вид

Z = z0 + ∂∂xz (x0 , y0 )(x − x0 )+ ∂∂yz (x0 , y0 )(y − y0 ),

где z0 = f (x0 , y0 ).

Доказательство

Напомним, что функция двух переменных z = f (x, y) задает в пространстве с введенной декартовой системой координат некоторую поверхность.

Уравнение плоскости, проходящей через точку M 0 (x0 , y0 , z0 ), имеет вид: A(x − x0 )+ B (y − y0 )+C (z − z0 )= 0 . Если C ≠ 0 , то можно разрешить это уравнение относительно переменной z , тогда получим уравнение z = z0 + a (x − x0 )+b (y − y0 ),

где a = − CA , b = − CB .

22

точке (x0 , y0 ).

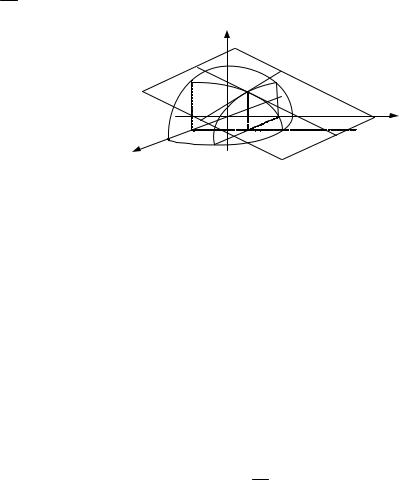
Ясно, что обе эти касательные прямые принадлежат искомой касательной плоскости

касательной плоскости к поверхности z = f (x, y) в точке (x0 , y0 ) при a = ∂∂xz (x0 , y0 ) и b = ∂∂yz (x0 , y0 ).

установить, что

dz = ∂∂xz (x0 , y0 ) x + ∂∂yz (x0 , y0 ) y = z − z0 ,

23