- •11.Основные законы гидродинамики.Уравнение неразрывности струи
- •26.Торема гаусса и применение
- •27.Электрическое поле заряженной плоскости плоскость
- •28.Электрическое поле заряженной сферы сфера
- •29.Электрическое поле заряженной нити
- •30.Диэлектрики в электрическом поле .Явление поляризации диэлектриков
- •31.Постоянный электрический ток.Закон Ома и Джоуля-Ленца
- •32.Правило Киргофа
- •33.Магнитное поле.Понятие о магнитной индукции.ЗаконБио-саввара –лапаса
- •34.Магнитное поле прямого тока.Магнитное поля кругового тока.
- •35.Понятие магнитного потока.Сила Ампера
- •36.Закон полного тока
- •37.Уравнение Максвелла
- •§1.3. Второе уравнение Максвелла.
- •§1.4. Третье уравнение Максвелла. Закон сохранения заряда.
- •§1.5. Четвертое уравнение Максвелла.
- •38.Волны и их виды.Уравнение плоской волны.Энергия волны
- •39.Звуковые волны их характеристики.
- •40.Явление интерференции.Усл. Макс и мин
- •41.Примеры интерференции света.Меьод Юнга, в тонких пленках, кольца Ньютона
- •43.Дифракция света.Зоны Френеля
- •43.Дифракционная решетка.Угловая и линейная дисперсия.Разрешающая способность
- •44.Явление поляризации свтеа.ЗаконыБрюстера, Малюса
- •45.Двойноелучеприломление света
- •46.Тепловое излучение тела.Законыкиргофа, стефана-больцмана и вина
- •47.Ультрафиолетовая катастрофа, формула планка, квантовая природа излучения
- •48.Основы голографии.Получ. Голографич. Изображ. И их воспроизв.
- •49.Внешний фотоэффект.Уравн. Энштейна для фотоэфекта.Многофотонныйвнешн. Эффект.
- •50.Внутренний фотоэффект
- •51.Рентгеновские лучи, методы получения.Эффекткомптона.Давление света
- •52.Атом резерфорда –бора.Энергия атома водорода и водородоподобных атомов
- •53.Спектры излучения и поглощения атома водорода
- •54.Корпускулярно-волновой дуализм.Гипотеза де-бройля
- •55.Соотношение неопределенностей
- •56.Уравнение шреденгера.Волновая функция и ее физ. Смысл
- •57.Квантование энергии электрона в потенциальной яме.
- •58.Квантовые генераторы.Принцип работы
- •59.Основы зонной теории вещ-ва-проводники, диэлектрики полупрводники
- •60.Собственная и примесная проводимость полупроводников
- •61.Пи-н переход.Свой-ва
- •62.Полупроводниковый диод.Транзистор.Принцип работы
- •63.Строение ядра атома.Деффектмассы,энергия связи
- •64.Явление радиоактивности.З.Радиоактивного распада
- •65.Алфа бетта гамма распады
- •66.Ядерная реакция.Энергия ядерных реакций
56.Уравнение шреденгера.Волновая функция и ее физ. Смысл

олнова́яфу́нкция,
или пси-функция ![]() —комплекснозначная
функция, используемая вквантовой
механикедля описаниячистого
состояния системы. Является
коэффициентом разложениявектора
состоянияпо базису (обычно
координатному):
—комплекснозначная
функция, используемая вквантовой
механикедля описаниячистого
состояния системы. Является
коэффициентом разложениявектора
состоянияпо базису (обычно
координатному):
Физический смысл волновой функции
В
координатном представлении волновая
функция ![]() зависит
от координат (или обобщённых координат)
системы. Физический смысл приписывается
квадрату её модуля
зависит
от координат (или обобщённых координат)
системы. Физический смысл приписывается
квадрату её модуля![]() ,
который интерпретируется как
плотностьвероятности
,
который интерпретируется как
плотностьвероятности![]() (для
дискретных спектров — просто
вероятность) обнаружить систему в
положении, описываемом координатами
(для
дискретных спектров — просто
вероятность) обнаружить систему в
положении, описываемом координатами![]() в
момент времени
в
момент времени![]() :
:
![]() .
.
Тогда
в заданном квантовом состоянии системы,
описываемом волновой функцией ![]() ,
можно рассчитать вероятность
,
можно рассчитать вероятность![]() того,
что частица будет обнаружена в любой
областиконфигурационного
пространстваконечного
объема
того,
что частица будет обнаружена в любой
областиконфигурационного
пространстваконечного
объема![]() :
:![]()
![]() .
.
Следует также отметить, что возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.
57.Квантование энергии электрона в потенциальной яме.
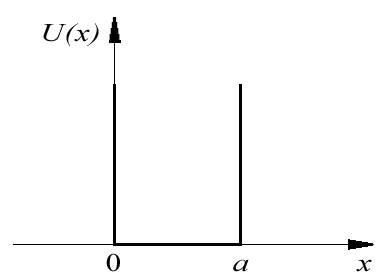
Рассмотрение стационарных задач квантовой механики начнем с наиболее простой для анализа задачи - о движении частицы в потенциальной яме с непроницаемыми, т.е. бесконечно высокими стенками. Такие ямы называют еще потенциальными ящиками, наиболее часто это название применяется по отношению к трехмерной потенциальной яме. Выявленные при этом особенности движения, такие, например, как квантование энергии, вырождение энергетических уровней и т.д. в дальнейшем будут проанализированы для случая ямы конечной глубины.
Одномерная
потенциальная яма. Рассмотрим
частицу, находящуюся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками. В этом
случае потенциальная энергия
частицы ![]() имеет
вид
имеет
вид
![]()
![]()
т.е.
внутри ямы (![]() )
потенциальная энергия
)
потенциальная энергия![]() постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
|
|
|
Рис. 4.1. |
Запишем
уравнение Шредингера для одномерного
движения частицы вдоль оси ![]()
|
|
(4.11) |
Поскольку
вне ямы потенциальная энергия обращается
в бесконечность, то для того, чтобы
выполнялось уравнение (4.11),
необходимо, чтобы вне ямы волновая
функция![]() обращалась
в ноль, т.е.
обращалась
в ноль, т.е.![]() .
Это означает, что в случае ямы с бесконечно
высокими стенками частица не может
выйти за пределы ямы, поскольку такие
стенки являются непроницаемыми для
частицы. В силу непрерывности волновая
функция
.
Это означает, что в случае ямы с бесконечно
высокими стенками частица не может
выйти за пределы ямы, поскольку такие
стенки являются непроницаемыми для
частицы. В силу непрерывности волновая
функция![]() должна
обращаться в нуль и на границах ямы:
при
должна
обращаться в нуль и на границах ямы:
при![]() и
при
и
при![]() .
.
Таким образом, задача о движении частицы в яме сводится к решению уравнения
|
|
(4.12) |
с граничными условиями
![]()
Введем обозначение
|
|
(4.13) |
При этом уравнение (4.12)принимает вид хорошо известного из теории колебаний уравнения
![]()
решение которого есть
|
|
(4.14) |
Используя
граничное условие ![]() ,
получаем
,
получаем
![]()
откуда
следует, что ![]() ,
где
,
где![]() .
Отметим, что при четных значениях
.
Отметим, что при четных значениях![]() и
при
и
при![]()
![]() ,
а при нечетных значениях
,
а при нечетных значениях![]()
![]() .
Однако, физический смысл имеет не сама
волновая функция
.
Однако, физический смысл имеет не сама
волновая функция![]() ,
а квадрат ее модуля
,
а квадрат ее модуля![]() ,
который от выбора значения
,
который от выбора значения![]() ,
т.е. от знака
,
т.е. от знака![]() не
зависит. Поэтому без потери общности
можно считать, что
не
зависит. Поэтому без потери общности
можно считать, что![]() .
.
Второе
граничное условие ![]() приводит
к соотношению
приводит
к соотношению
![]()
которое
для ![]() выполняется
при
выполняется
при
|
|
(4.15) |
Отметим,
что значение ![]() ,
формально также входящее в решение(4.14),
не удовлетворяет условию задачи, т.к.
при этом
,
формально также входящее в решение(4.14),
не удовлетворяет условию задачи, т.к.
при этом![]() ,
что означает, что частица в яме
отсутствует. Поэтому значение
,
что означает, что частица в яме
отсутствует. Поэтому значение![]() следует
отбросить.
следует
отбросить.
Подставляя (4.13)в(4.15), приходим к выражению для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками
|
|