Введение

Настоящее время характерно резким расширением приложений математики, во многом связанным с созданием и развитием средств вычислительной техники.

Распространенное мнение о всемогуществе современных ЭВМ часто порождает впечатление, что математики избавились почти от всех хлопот, связанных с численным решением задач, и разработка новых методов для их решения уже не столь существенна. В действительности дело обстоит иначе, поскольку потребности эволюции, как правило ставят перед наукой задачи, находящиеся на грани её возможностей.

Требование численного решения новых задач привело к появлению большого количества новых методов.

Просмотр методов решения сложных прикладных задач показывает, что, как правило, эффект, достигаемый за счет совершенствования численных методов, по порядку сравним с эффектом, достигаемым за счет повышения производительность ЭВМ.

1 Погрешность вычислений

Погрешность решения задачи обуславливается следующими причинами:

1. Математическое описание задачи является не точным, в частности не точно заданы исходные данные описания.

2. Применяемый для решения метод часто не является точным: получение точного решения, возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, поэтому вместо точного решения задачи приходится прибегать к приближенному.

3. При вводе данных в машину, при выполнении арифметических операций и при выводе

Погрешности, соответствующие этим причинам, называют

1. неустранимой погрешностью,

2. погрешностью метода,

3. вычислительной погрешностью.

2 Задача приближения функции

Приближением функции f(x) называют замену данной функции f(x) функцией y=g(x), значения которой близки к значениям исходной функции.

При этом функция f(x) называется приближаемой, а функция g(x)- приближающей.

Потребность приближения функции возникает в 2х случаях:

1. Если функция y=f(x) задана таблично или графически и требуется подобрать аналогичное выражение.

2. Если функция y=f(x) имеет громоздкий вид и требуется заменить её на более простую для сокращения времени работы с ней.

Задача приближения функции может быть следующих видов:

1. Равномерное приближение

В этом случае приближающая функция g(x) ищется в таком виде, что бы её максимальное отклонение от f(x) не превышала заданной точности ε.

2. Среднеквадратичное приближение

а) точечное – в случае, если f(x) задана таблицей.

интегральное – в случае, если f(x) задана выражением.

2.1 Задача интерполирования

Интерполирование – такое приближение f(x) функцией g(x), при котором значения приближающей функции не просто близки, а совпадают со значениями приближаемой функции в отдельно взятых точках x₁…x_m.

Точки Х₁-Х_m так же называют узлами интерполяции.

Если исходная функция y=f(x) представлена в виде таблицы значений:

X1	X2	X3	………	Xm
Y1	Y2	Y3	………	Ym

то приближающая функция g(x) ищется в виде интерполяционного многочлена P_n(x).

При этом ;

Таким образом для каждого узла интерполяции можно записать:

При этом должно выполнятся условие единственности интерполяционного многочлена: m=n+1.

Интерполяционный многочлен можно представить в форме Лагранжа:

.

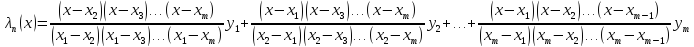Рассмотрим остаточный член: , x ∈ [a, b]. По определению интерполяционного полинома  поэтому речь идет об оценке при значениях . Пусть имеет непрерывную (n+1) производную на отрезке [a, b]. Тогда погрешность определяется формулой: , где , - точка из [a, b]. Так как точка наизвестна, то эта формула позволяет только оценить погрешность: где  Из вида множителя следует, что оценка имеет смысл только при . Если это не так, то при интерполяции используются полиномы низких степеней (n = 1,2).