
Решение
Проведем процесс
ортогонализации Грама-Шмидта системы
векторов
![]() базиса
базиса
![]() .
.
1) На
первом шаге необходимо вычислить векторы
![]() .
Вычисляем
вектор
.
Вычисляем
вектор
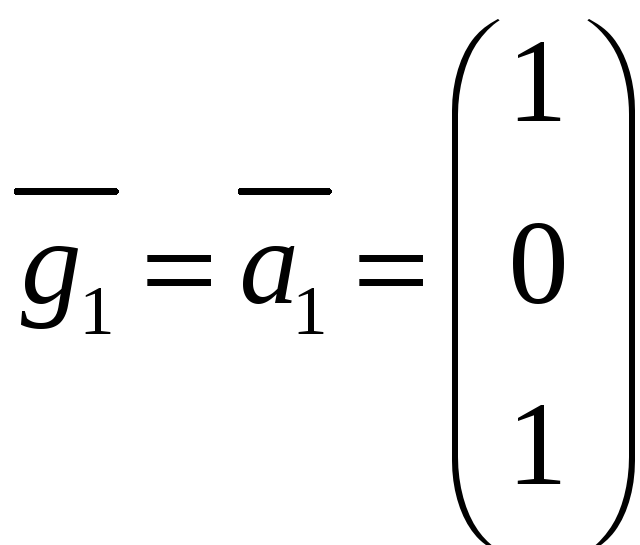 ,
,
затем скалярное
произведение и норму вектора
![]()
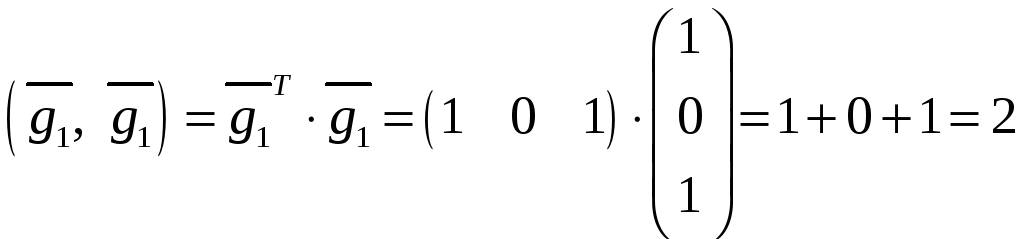 ,
,
![]() ,
,
и окончательно вектор
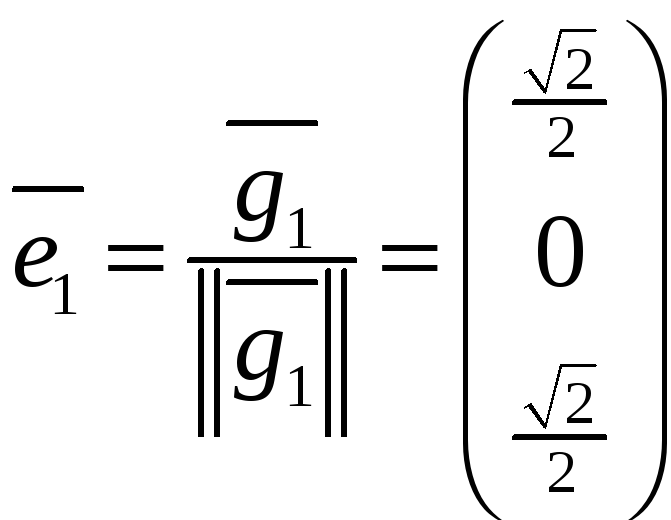 ,
,
![]() .
.
2) На втором шаге
необходимо вычислить векторы
![]() .
Сначала вычисляем скалярное произведение
.
Сначала вычисляем скалярное произведение
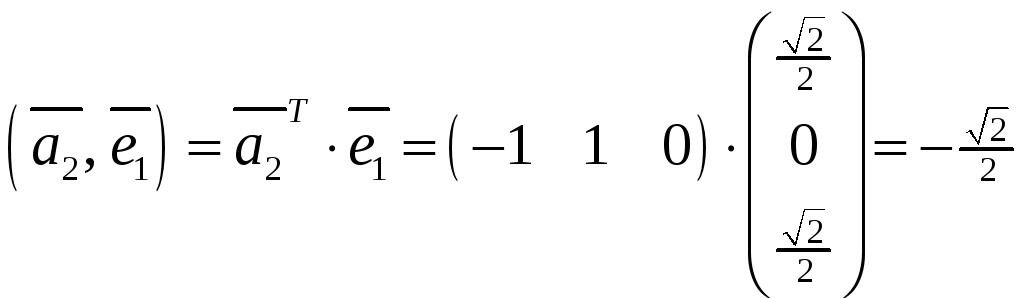 ,
,
затем вектор
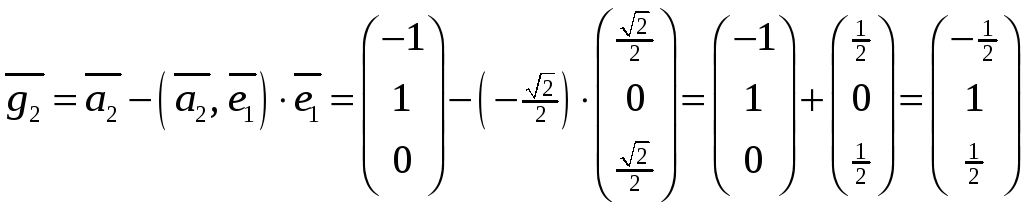 .
.
Теперь нормируем
вектор
![]() :
:
![]() ,
,
получаем вектор
![]()
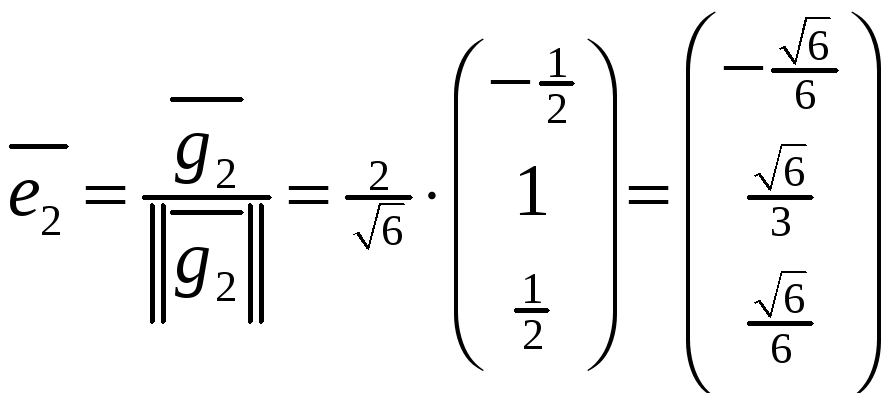 ,
,
![]() .
.
3) На третьем шаге
необходимо вычислить векторы
![]() .
Сначала вычисляем скалярные произведения
.
Сначала вычисляем скалярные произведения
![]() ,
,
![]() ,
,
затем вектор
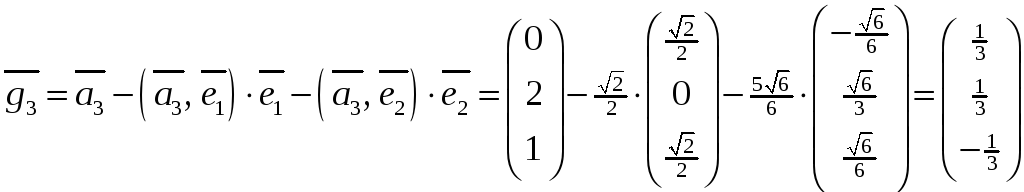 .
.
Теперь нормируем
вектор
![]() :
:
![]() ,
,
получаем последний искомый вектор
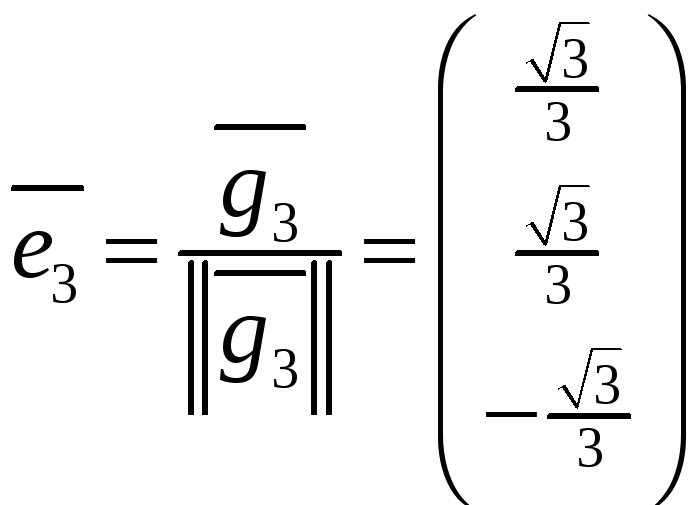 ,
,
![]() .
.
Итак, ортонормированный
базис
![]() состоит из векторов:
состоит из векторов:
![]()
![]() ,
,
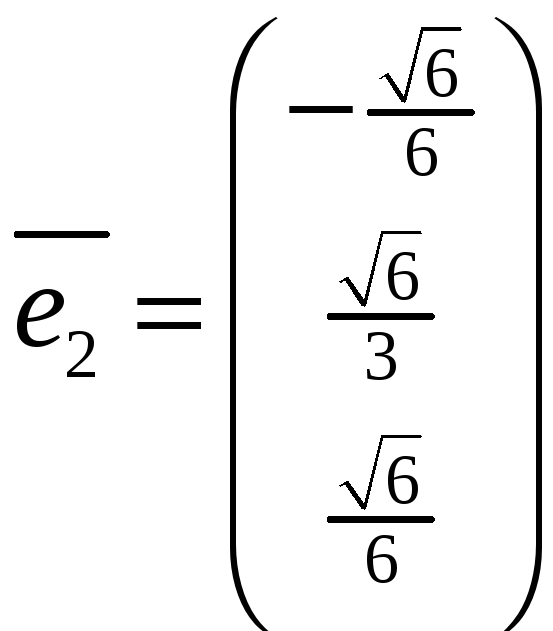 ,
,
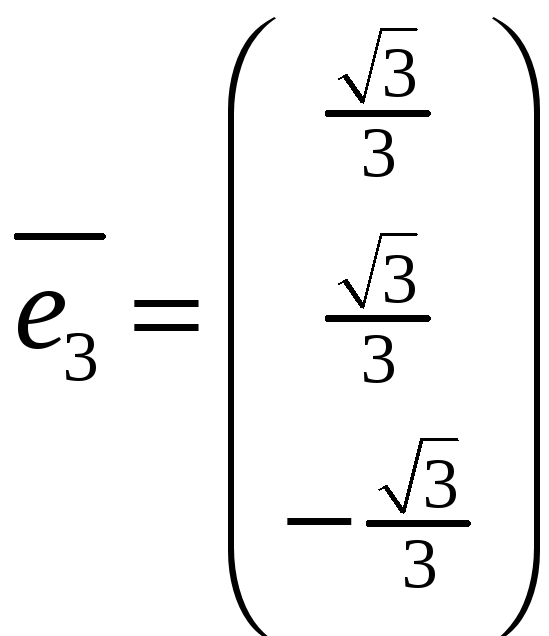 .
.
Пример
7.
Проверить
ортогональность векторов
![]() ,
,
![]() пространства
пространства
![]() и дополнить эти векторы до ортогонального
базиса:
и дополнить эти векторы до ортогонального
базиса:
![]() .
.
Решение. Решение
задачи
предусматривает
нахождение двух векторов
![]() ,
,
![]() таких, что система векторов
таких, что система векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() образует ортогональную систему векторов
в пространстве
образует ортогональную систему векторов
в пространстве
![]() ,
то есть при всех
,
то есть при всех
![]() (
(![]() )
)
![]() (любые два разных вектора из системы
ортогональны).
(любые два разных вектора из системы
ортогональны).
Проверим
ортогональность векторов
![]() ,
,
![]() .
Для этого вычисляем скалярное произведение
.
Для этого вычисляем скалярное произведение
![]() этих векторов:
этих векторов:
![]() .
.
Так как
![]() ,
то векторы
,
то векторы
![]() ,
,
![]() ортогональны.
ортогональны.
Найдем вектор
![]() такой, что он ортогонален векторам
такой, что он ортогонален векторам
![]() ,
,
![]() ,
то есть
,
то есть
![]() .
В результате приходим к системе уравнений
.
В результате приходим к системе уравнений
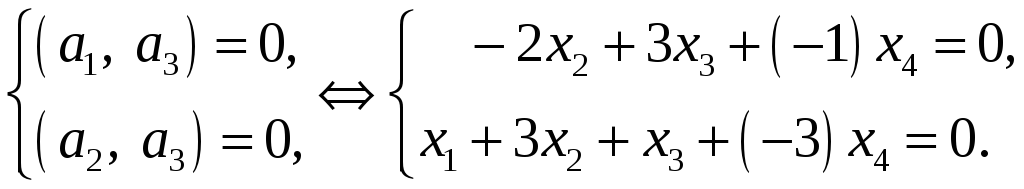
Эту однородную систему решим методом Гаусса. Приводим матрицу системы к ступенчатому виду (меняем местами строки матрицы)
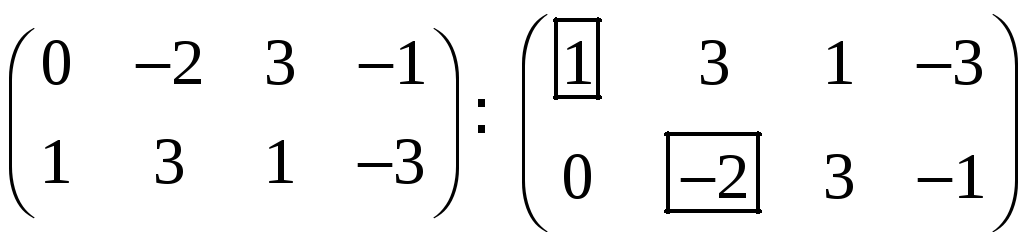 .
.
Ранг матрицы
![]() .
Принимая переменные
.
Принимая переменные
![]() за базисные, а
за базисные, а
![]() за свободные (обозначаем при этом
за свободные (обозначаем при этом
![]() ),
получим общее решение рассматриваемой
ОСЛАУ
),
получим общее решение рассматриваемой
ОСЛАУ
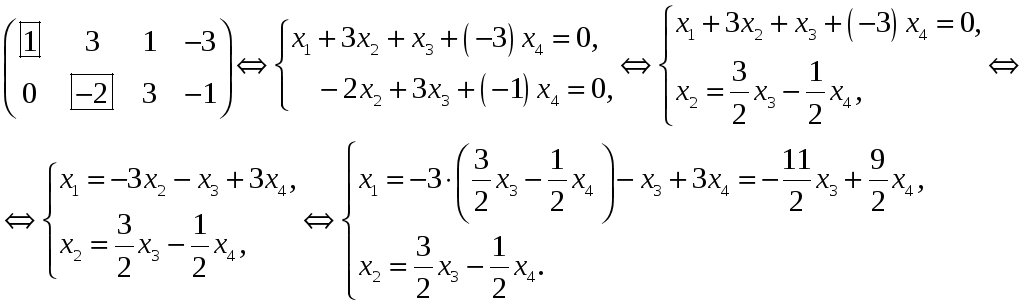
Итак, общее решение однородной системы имеет вид
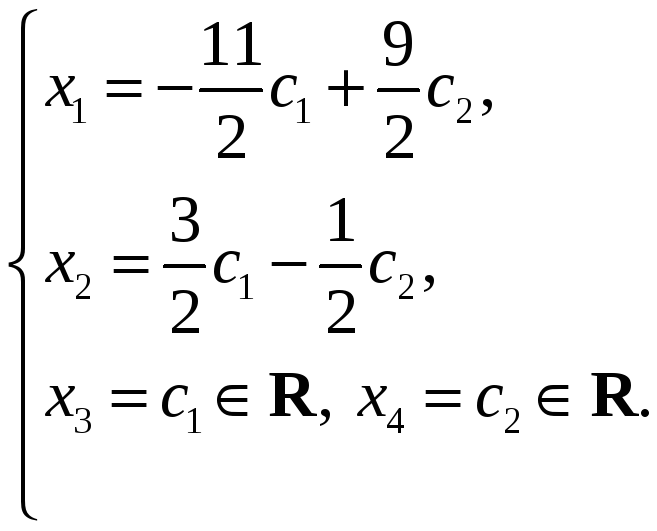
Из множества
решений выделим частное решение. Положим
(для дальнейшего удобства)
![]() .
Тогда получим
.
Тогда получим
![]() .
Итак, вектор
.
Итак, вектор
![]() имеет вид
имеет вид
![]() .
.
Выполним проверку:
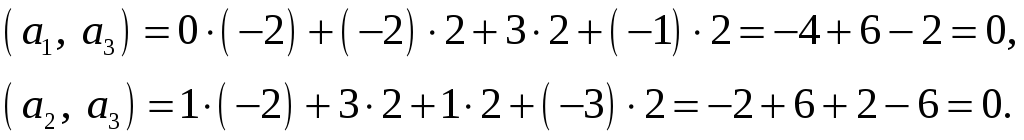
Найдем вектор
![]() такой, что он ортогонален векторам
такой, что он ортогонален векторам
![]() ,
,
![]() ,
,
![]() ,
то есть
,
то есть
![]() .
В результате приходим к системе уравнений
.
В результате приходим к системе уравнений
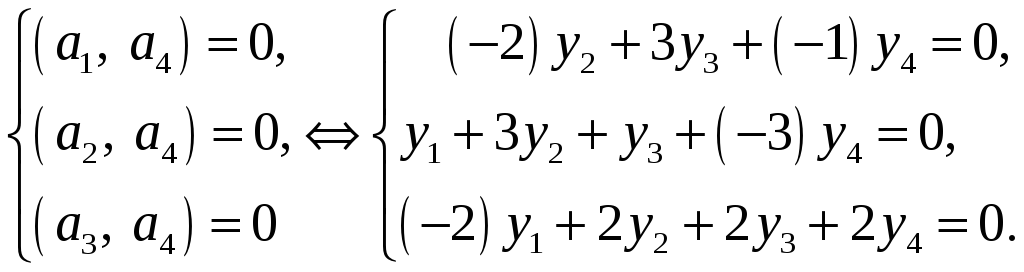
Эту однородную систему решим методом Гаусса. Приводим матрицу системы к ступенчатому виду

Ранг ступенчатой
матрицы
![]() .
Принимая переменные
.
Принимая переменные
![]() за базисные, а
за базисные, а
![]() - за свободную (обозначаем при этом
- за свободную (обозначаем при этом
![]() ),
получим общее решение рассматриваемой
ОСЛАУ
),
получим общее решение рассматриваемой
ОСЛАУ
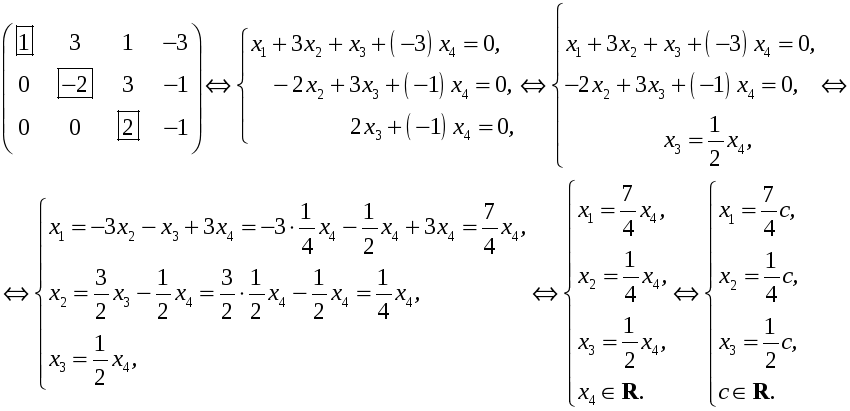
Из множества
решений выделим частное решение. Положим
(для дальнейшего удобства)
![]() .
Тогда получим
.
Тогда получим
![]() .
Итак, вектор
.
Итак, вектор
![]() имеет вид
имеет вид
![]() .
.
Выполним проверку:
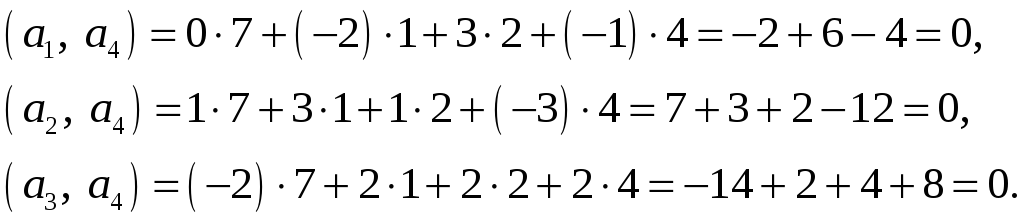
Ответ: ортогональный базис имеет вид
![]() ,
,
![]() ,
,
![]() .
.
