Praktikum_ЛО

9

Практикум. Линейные операторы

В данном практикуме рассматриваются следующие задачи:

1) нахождение матрицы линейного оператора;

2) описание структуры линейного оператора (нахождение ранга, дефекта, образа и ядра);

3) вычисление собственных значений и собственных векторов линейного оператора (матрицы линейного оператора).

Примеры задач, рассматриваемых в данном практикуме, соответствуют заданиям 6, 7, 8 типового расчета (индивидуальных заданий).

Пример 1.

1. Найти матрицу линейного оператора , переводящего вектор в вектор

в стандартном базисе

линейного пространства .

2. Описать его структуру (образ, ранг, ядро, дефект, найти базисы образа и ядра оператора).

Решение.

1. Находим образы векторов :

Итак, образы базисных векторов базиса имеют вид

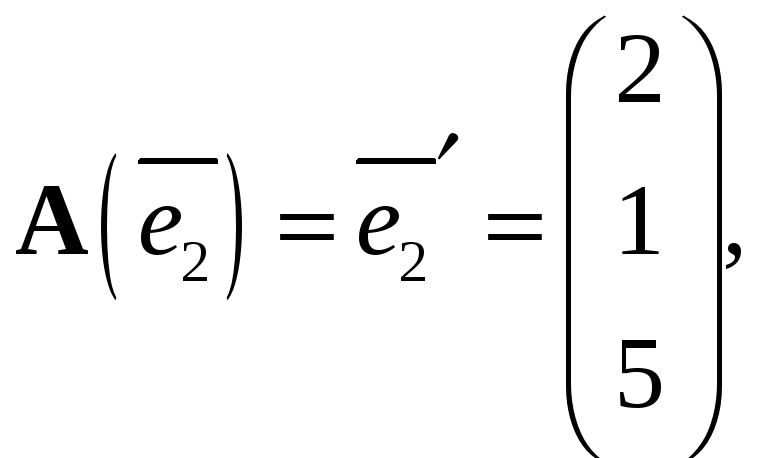
Для составления матрицы линейного оператора в базисе найдем коэффициенты разложения векторов через базисные векторы :

Составляем матрицу линейного оператора, столбцами которой являются коэффициенты разложения векторов через базисные векторы :

.

2) Для нахождения ядра

оператора необходимо решить однородную систему уравнений

с основной матрицей . Решение проводим методом Гаусса.

Выписываем матрицу и при помощи элементарных преобразований приводим ее к ступенчатому виду:

Переходя от ступенчатой матрицы к системе уравнений, получим

Так как ранг ступенчатой матрицы равен 2, система имеет бесконечное множество решений. В качестве базисных (основных) переменных выберем переменные (при этом является свободной переменной). Выражая базисные переменные через свободную , получим

Итак, ядро оператора состоит из всех векторов вида

.

Взяв , получим базис в ядре, состоящий из одного вектора

.

Так как базис ядра состоит из одного вектора, то размерность ядра (дефект оператора) равен 1:

Размерность образа оператора (ранг оператора) равна

.

Для нахождения базиса образа достаточно взять из векторов любые два вектора, у которых координаты (компоненты) не пропорциональны. Например, базисными векторами в образе являются векторы

Собственные значения и собственные векторы линейного оператора

(матрицы линейного оператора)

Напомним основные понятия лекции “Собственные значения и собственные векторы линейного оператора”.

Пусть в линейном пространстве задан линейный оператор .

Определение. Ненулевой вектор , удовлетворяющий условию (операторному равенству)

, , (1)

называется собственным вектором оператора . Число при этом называется собственным значением (собственным числом) оператора , соответствующим собственному вектору .

Выберем в пространстве некоторый базис и пусть оператору в этом базисе соответствует матрица . Тогда операторное равенство (1) можно переписать в матричном виде

, ,

или в виде системы уравнений

(2)

Так как нас интересуют нетривиальные решения системы (2) (поскольку собственный вектор по определению должен быть ненулевым), то основная матрица системы (2)должна быть вырожденной, то есть

.

Определение. Уравнение

(3)

называется характеристическим уравнением оператора .

Разложив определитель в уравнении (3), получим многочлен

(4)

-ой степени относительно . Многочлен (4) называется характеристическим многочленом оператора , его корни – характеристическими корнями многочлена (4).

Теорема. Для того чтобы число являлось собственным значением линейного оператора , необходимо и достаточно, чтобы оно было корнем характеристического уравнения (3) этого оператора.

Определение. Алгебраической кратностью собственного значения линейного оператора называется кратность корня характеристического уравнения (3) (кратность характеристического многочлена ).

Кратностью корня называется натуральное число такое, что

, , …, , .

Алгоритм вычисления собственных векторов линейного оператора

1) Зафиксировать произвольный базис линейного пространства и найти матрицу оператора в этом базисе;

2) Составить и решить (в множестве действительных или комплексных чисел) характеристическое уравнение (3). Его действительные корни и есть собственные значения оператора;

3) При каждом найденном собственном значении однородная система (3) будет иметь ненулевые решения. Выделив фундаментальную систему линейно независимых решений, получим либо единственный собственный вектор , либо систему r линейно независимых собственных векторов оператора, соответствующих собственному значению .

Пример 2. Задана матрица

некоторого линейного оператора в базисе пространства . Найти собственные значения и соответствующие собственные векторы оператора.

Решение. Матрица линейного оператора в базисе пространства уже задана. Для нахождения собственных значений составляем характеристическое уравнение (3):

.

Вычислим определитель:

.

Итак, получаем следующее характеристическое уравнение оператора

.

Его корни – собственные значения (решаем квадратное уравнение):

Алгебраическая кратность каждого собственного значения равна одному, так как каждый корень характеристического уравнения повторяется единожды.

Соответствующая однородная система (2) имеет вид

(5)

Полагая в системе (5) , получим однородную систему

(удаляем из однородной системы второе уравнение, так как оно равносильно первому уравнению), общее решение которой имеет вид

Находим соответствующую фундаментальную систему решений (положим число любым ненулевым числом, для удобства возьмем )

.

Аналогично положим в системе (5) . Получим однородную систему

(удаляем из однородной системы первое уравнение, так как оно равносильно второму уравнению), общее решение которой имеет вид

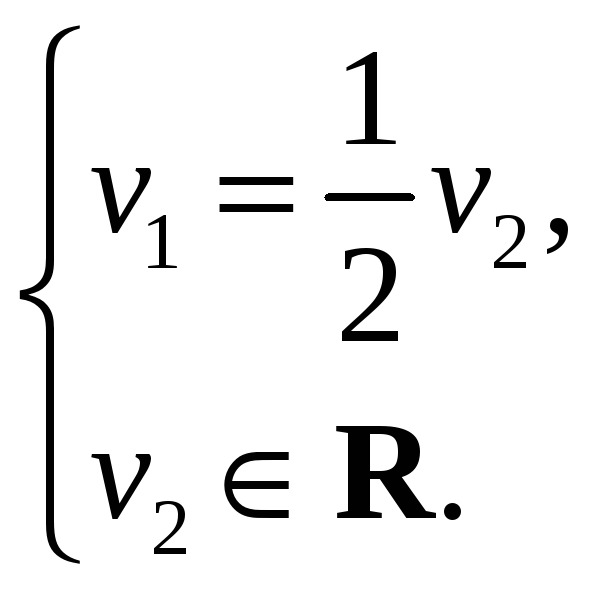
Находим соответствующую фундаментальную систему решений (положим число любым ненулевым числом, для удобства возьмем )

.

В заключение, выполним проверку. Убедимся в справедливости равенств

, .

Имеем

Пример 3. Задана матрица

некоторого линейного оператора в базисе пространства . Найти собственные значения и соответствующие собственные векторы оператора.

Решение. Матрица линейного оператора в базисе пространства уже задана. Для нахождения собственных значений составляем характеристическое уравнение (3):

.

Разложим определитель по первой строке:

Итак, получаем следующее характеристическое уравнение оператора

Его корни – собственные значения:

записанные с учетом алгебраических кратностей. Алгебраическая кратность собственного числа равна двум, так как данный корень повторяется дважды. Алгебраическая кратность собственного числа равна одному, так как данный корень повторяется однократно.

Соответствующая однородная система (2) имеет вид

(6)

Полагая в системе (6) , получим однородную систему

Решим полученную однородную систему при помощи метода Гаусса. Составляем основную матрицу этой системы и при помощи элементарных преобразований приводим ее к ступенчатому виду

Ранг полученной матрицы равен 1, в качестве базисной переменной удобно взять переменную , а в качестве свободных – переменные . Выражая через , получим общее решение

Находим соответствующую фундаментальную систему решений. Положим сначала , получим соответственно и вектор-столбец

.

Положим затем , получим соответственно и вектор-столбец

.

Вектор-столбцы есть координатные вектор-столбцы собственных векторов , отвечающих собственному числу .

Аналогично, положив в системе (6) , получим однородную систему

Решим полученную однородную систему при помощи метода Гаусса. Составляем основную матрицу этой системы и при помощи элементарных преобразований приводим ее к ступенчатому виду

Ранг полученной ступенчатой матрицы равен 2, в качестве базисных переменных удобно взять переменные , а в качестве свободной – переменную . Выражая через , получим общее решение

Положив в общем решении , получим координатный вектор-столбец

собственного вектора .

В заключение, выполним проверку. Убедимся в справедливости равенства

.

Имеем

Проверка равенств , проводится аналогично.

Практикум №2. Линейные операторы