
pdm_02
.pdf
Совершенная конъюнктивная нормальная форма (СКНФ)
Определение. СКНФ – это такая форма КНФ, что:
-в ней нет одинаковых дизъюнктивных термов;
-каждый терм содержит все аргументы в прямом или инвертированном виде
в одинаковом порядке следования. Пример.
x |
y |
z |
f (x, y, z) |
термы |
||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
(x |
y |
z) |
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
(x |
y |
z) |
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
(x |
y |
z) |
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
(x |
y |
z) |
|
|
|
|
|
|
|
Алгоритм. Получение СКНФ по таблице истинности.
1.Выбираем строки, где f(…)=0.
2.Записываем дизъюнктивные термы для строк выбранных по (1) так, чтобы они были равны нулю,
т.е. для xi=0 берѐм xi, для xi =1 берѐм ¬xi.
3.Объединяем все полученные по
(1) и (2) термы в СКНФ.
f (x, y, z) (x y z) (x y z) (x y z) (x y z) |
21 |

Совершенная дизъюнктивная нормальная форма (СДНФ)
Определение. СДНФ – это такая форма ДНФ, что:
-в ней нет одинаковых конъюнктивных термов;
-каждый терм содержит все аргументы в прямом или инвертированном виде
в одинаковом порядке следования. Пример.
x |
y |
z |
f (x, y, z) |
термы |
||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
(x |
y |
z) |
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
(x |
y |
z) |
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
(x |
y |
z) |
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
(x |
y |
z) |
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
Алгоритм. Получение СДНФ по таблице истинности.
1.Выбираем строки, где f(…)=1.
2.Записываем конъюнктивные термы для строк выбранных по (1) так, чтобы они были равны единице, т.е. для xi=0 берѐм ¬xi, для xi =1
берѐм xi.
3. Объединяем все полученные по
(1) и (2) термы в СКНФ.
f (x, y, z) (x y z) (x y z) (x y z) (x y z) |
22 |
|
|
|
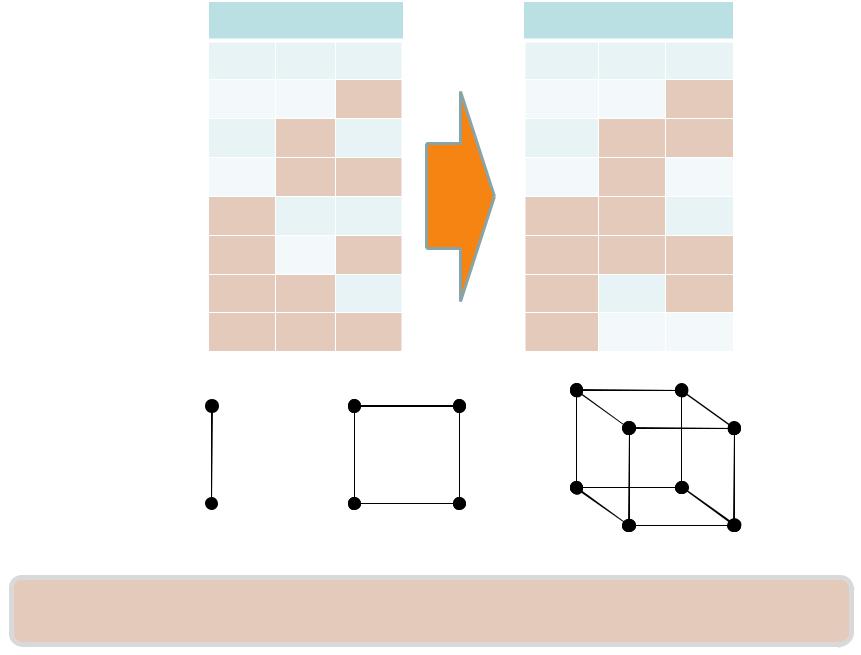
Код Грея |
|
|
|
обычный код |
|
|
код Грея |
|
||
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
00 |
10 |
100 |
|
110 |
|
|
|
010 |
|||
|
|
|
|
|
000 |
|
1 |
|
01 |
11 |
101 |
|
111 |
|
|
|
011 |
|||
|
|
|
|
|
001 |
|
При переходе в смежные вершины графа или соседние строки таблицы
значение элемента кода Грея изменяется лишь в одном разряде. |
23 |
|
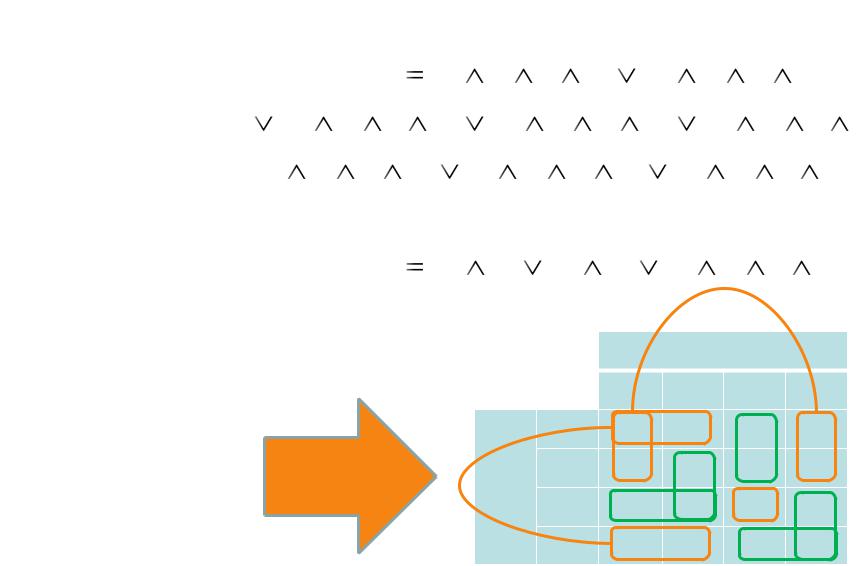
Карты Карно
Карты Карно – табличный способ выражения функции алгебры логики с заданием порядка расположения аргументов в порядке кода Грея по двум измерениям. Карты Карно – разновидность таблицы истинности.
x |
y |
z |
s |
f(x,y,z,s) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
СДНФ по таблице истинности :
f (x, y, z, s) (x y z s ) (x y z s) 
(x y z s ) (x y z s ) (x y z s )  (x y z s ) (x y z s) (x y z s)
(x y z s ) (x y z s) (x y z s)
ДНФ по карте Карно:
f (x, y, z, s) ( y z) (x s ) (x y z s)
|
|
|
xy |
|
|
|
00 |
01 |
11 |
10 |
|
00 |
1 |
1 |
0 |
1 |
|
01 |
1 |
0 |
0 |
1 |
|
zs |
|
|
|
|
|
11 |
0 |
0 |
1 |
0 |
|
10 |
1 |
1 |
0 |
0 |
24 |
|

Принципы минимизации функций на базе карт Карно
Получение ДНФ |
|
|
|
|
|
|
|
|
||||||||
(x |
f ( )) (x f ( ))... ... |
f ( )... |
|
|
|
|
|
|||||||||
Получение КНФ |
|
|
|
|
|
|
|
|
||||||||
(x |
f ( )) (x f ( ))... ... |
f ( )... |
|
|
|
|
|
|||||||||
противоречие : |
x x |
0, исключение третьего : x x 1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
...f ( ) |
(x |
...f ( )) (x f (...)) |
(x |
...f ( )) (x f (...)) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
f (... |
) |
|
|
f (... |
) |
|
|
f (... |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
f (... |
) |
|
|
f (... |
) |
|
|
f (... |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
f (... |
) |
|
|
f (... |
) |
|
|
f (... |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
f (... |
) |
|
|
f (... |
) |
|
|
f (... |
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения аргументов в соседних клетках в карты Карно отличаются только в одном разряде.
25
Принципы объединения клеток карт Карно
#Объединять клетки можно по единицам для ДНФ или по нулям для КНФ.
#Объединять возможно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число.
#При объединении клеток 2n из терма исключается n аргументов.
#Область, которая подвергается объединению должна содержать только единицы или только нули.
#Можно объединять только области с симметричными (в смысле кода Грея) аргументами отличающиеся только одним разрядом.
#Исключаемые при минимизации аргументы должны содержаться в выделенной области в равном количестве в прямом и инвертированном виде.
#Можно объединять, не смежные клетки.
#Все единицы (либо нули) должны попасть в какую-либо область, а значит и в какой либо терм.
#При объѐдинении возможно повторное использование клеток, но каждая область должна содержать клетки принадлежащие только ей.
#Для минимизации ДНФ или КНФ число клеток в области должно быть максимально, а количество областей возможно меньшее, т.к. каждая область соответствует терму.
26
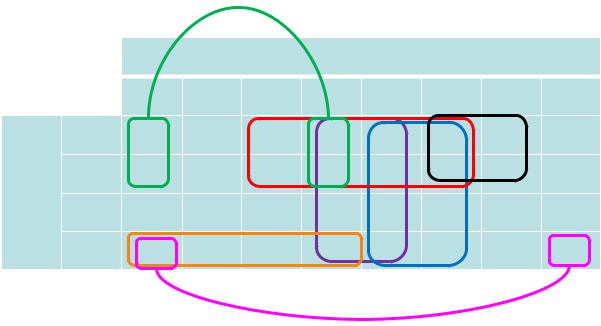
Карты Карно, минимизация функций алгебры логики
Пример.
Минимизация функции пяти переменных при помощи карты Карно. Формирование ДНФ.
ДНФ: f(x,y,z,s,p)=
=(y ¬s)v v(y ¬z)v v(xy)v v(xz ⌐s)v
v(⌐x ⌐z ⌐s)v v(⌐xs ⌐p)v v(⌐y ⌐zs ⌐p)
|
|
|
|
xyz |
|
|
|
|
|
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
00 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
01 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
sp |
|
|
|
|
|
|
|
|
11 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
10 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
27

Элементы формальной логики, умозаключения
Умозаключение состоит из совокупности утверждений, называемых гипотезами, или посылками, и утверждения, называемого заключением.
Правильным умозаключением называется такое умозаключение, которое истинно всякий раз, когда истинны его гипотезы.
От противного p q
q
p
Расширение p
p r
Выбор p
p (r s)
rq
sq
q
Сведение к абсурду p (q q )
H1
H2 гипотезы
H3
C заключение
Правило отделения p → q
p
q
Силлогизм p → q
p → r
p → r
p |
28 |
|

Предикаты, кванторы
Предикат – есть функция, определѐнная на некотором множестве и принимающая значения истина (true↔1) или ложь (false↔0). Все переменные предиката свободные.
Пусть P(x, x1, x2 ,..., xk ) есть (k +1) |
местный предикат, |
определѐнный на множестве D. |
Тогда для xi D : |
запись ( x)P(x, x1, x2 ,..., xk ) означает: "существует такой |
|
элемент x из D, для которого |
P(x, x1, x2 ,..., xk ) ↔ истинно"; |
запись ( x)P(x, x1, x2 ,..., xk ) означает: "для всех элементов
x из D, P(x, x1, x2 ,..., xk ) ↔ истинно".
Символ называют квантором существования. Символ называют квантором всеобщности.
Предикаты позволяют связать произвольные данные средствами двоичной логики в систему объединѐнную общим алгоритмом.
29

Формулы преобразования
1.( x)(P(x) ( x)(P(x)
2.( x)(P(x) ( x)(P(x)
Q(x)) |
( x)P(x) |
Q(x)) |
( x)P(x) |
Q(x)) |
( x)P(x) |
Q(x)) |
( x)P(x) |
( x)Q(x) ( x)Q(x) ( x)Q(x) ( x)Q(x)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
( x)P(x) |
( x)P (x), ( x)P(x) |
( x)P (x) |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
( x)P (x) |
( x)P(x), ( x)P (x) |
( x)P(x) |
||||||||||||
5. |
( x)(C P(x)) |
|
C ( x)P(x) |
|
|
|
|||||||||
|
( x)(P(x) |
C) |
|
( x)P(x) |
|
C |
|
|
|
||||||
6. |
( x)(C P(x)) |
|
C ( x)P(x) |
|
|
|
|||||||||
|
( x)(P(x) |
C) |
|
( x)P(x) |
|
C |
|
|
|
||||||
Формула A эквивалентна формуле B (A↔B) если для любого набора |
|
аргументов из допустимого множества взаимная замена формул не |
|
влияет на вычисляемый результат. |
30 |
|
