
pdm_06
.pdf
Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики
Дискретная математика
курс лекций лекция 6
Рекурсия, фракталы, цепные дроби, конечные
Кафедра «Проектирования и безопасности компьютерных систем» Гришенцев А. Ю. www.moveinfo.ru
разности
Санкт-Петербург
2014 |
1 |
|

Рекурсия
Определение (не строгое). Рекурсия – есть процесс определения (изображение, описание, формулировка) некоторого объекта с использованием самого себя.
Определение. Глубина рекурсии – это максимальная степень вложенности вызовов функций в ходе вычисления.
В математике и компьютерных науках рекурсивной называют функцию которая для своего определения использует саму себя.
Рекурсивная программа не может вызывать себя безконечно, поскольку в этом
случае она ни когда не завершится. |
2 |

Рекурсия вокруг нас
В окружающем нас мире рекурсия встречается всюду |
3 |
|
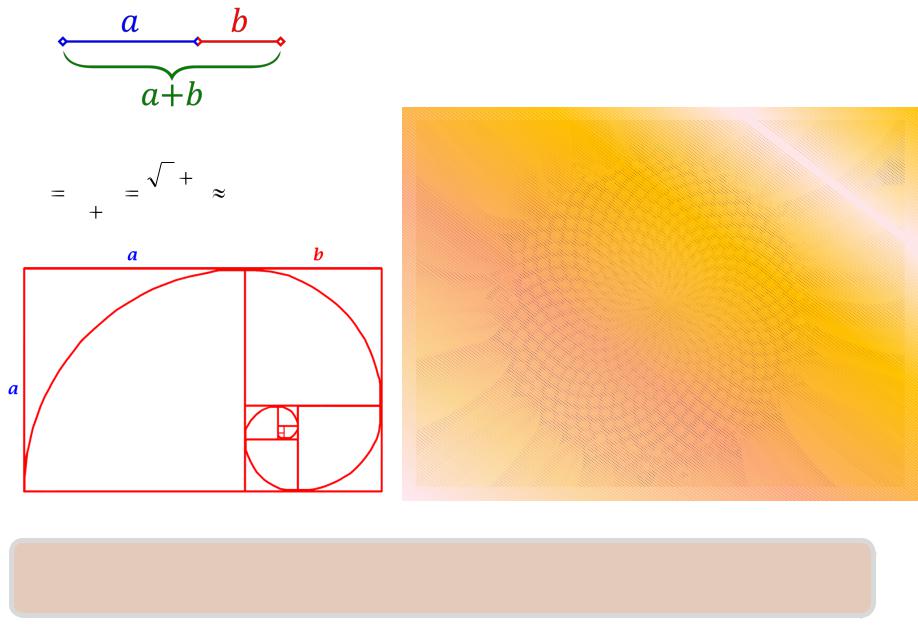
Золотое сечение
Пропорция золотого сечения
b |
|
a |
5 1 |
1,618033988 ... |
||
|
|
|
|
|
|
|
a |
|
a b |
2 |
|
||
|
|
|
||||
Пропорциональное отношение золотого сечения (или близкое к
нему) часто используется в искусстве и распространено в природе. 4

Рекурсия в форматах данных
// описание структуры узла struct node {
data_type data; // данные узла
node *next; |
|
// указатель на следующий узел |
||||||||
} |
|
|
|
|
|
|
|
|
|
|
Связанный, циклический список |
Связанный, ациклический список |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
data |
|
|
*next |
|
|
data |
|
*next |
|
|
|
|
|
|
|
|
|
|
|
|
data |
|
*next |
|
data |
|
*next |
|
|
|
|
|
|
|
data |
|
*next |
|
data |
|
*next |
|
|
|
|
|
|
|
Существует значительно большее многообразие организации списков, чем рассмотрено на данном слайде.
0
5

Некоторые рекурсивные функции
Определени е факториала |
|
|
|
|
Функция |
||||||
|
|
|
n |
|
|
|
|
|
|
|
|
n |
N |
|
n! |
n |
(0! |
1) |
|
|
A(m, n) |
||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
рекурсивно |
|
|
|
|
|
|
|
|
||
n |
N |
n! |
1, n |
0 |
|
|
|
|
|
|
|
n (n |
1)!, n |
0 |
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
Числа |
Каталана |
|
|
|
||||
|
|
|
Kat(n) |
|
|
(2n)! |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(n 1)!(n!) |
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
или рекурсивно |
|
|
|
|||||
|
|
|
Kat(n |
1) |
|
2(2n |
1) |
Kat(n) |
|||
|
|
|
|
(n |
2) |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Аккермана |
|
|
|
|
n 1, |
|
m |
0 |
|
A(m |
1,1), |
m |
0, n |
0 |
A(m |
1, A(m, n |
1)), m |
0, n |
0 |
Числа |
Фибоначчи |
|
|
|
|
|
|
|
|
|
|
||||||||
F (1) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (2) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (n) |
F (n 1) F (n |
2), |
|
n |
2 |
|
|
||||||||||||
или не |
рекурсивно : |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|||
F (n) |
1 1 |
|
5 |
1 |
|
|
1 |
5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Используя ранее вычисленные данные, в некоторых рекурсивных функциях, возможно существенно сократить объѐм расчѐтов.
На сходных принципах построен метод динамического программирования, который состоит в том, что задача разбивается на множество сходных подзадач, чтобы решить каждую подзадачу только один раз, сократив тем
самым общее количество вычислений. |
6 |
Линейные рекуррентные отношения
Определение. Рекурсивное отношение вида
an = c1(n)an-1 + c2(n)an-2 + c3(n)an-3 + . . . + cp(n)an-p + f(n)
называется линейным рекуррентным отношением порядка p.
Пример. xn = 2nxn-1 + nxn-2 + n2/2
Определение. Рекурсивное отношение вида
an = c1an-1 + c2an-2 + c3an-3 + . . . + cpan-p + f(n), cp ≠ 0
с постоянными коэффициентами ci ≠ 0 при 1 ≤ i ≤ p
называется линейным рекуррентным отношением с постоянными коэффициентами порядка p.
Пример. xn = 5xn-1 + 4xn-2 + n2/2
Определение. Рекурсивное отношение вида
an = c1(n)an-1 + c2(n)an-2 + c3(n)an-3 + . . . + cp(n)an-p
называется линейным однородным рекуррентным отношением порядка p.
Пример. xn = 2nxn-1 + nxn-2
Определение. Рекурсивное отношение вида
an = c1an-1 + c2an-2 + c3an-3 + . . . + cpan-p, cp ≠ 0
с постоянными коэффициентами ci ≠ 0 при 1 ≤ i ≤ p
называется линейным однородным рекуррентным отношением с постоянными коэффициентами порядка p.
Пример. xn = 5xn-1 + 4xn-2
7

Исключение рекурсии, простые примеры
С рекурсией
f (1) |
1 |
f (n) |
f (n 1) n2 |
Без рекурсии
n
f (n) i2
i 1
С рекурсией |
|
|
f (1) |
1 |
|
f (n) |
f (n 1) 2 |
|
Без рекурсии |
||
f (1) |
1 |
|
f (2) |
3 |
|
f (3) |
5 |
f (n) 2n 1 |
f (4) |
7 |
|
. . . |
|
|
С рекурсией |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f (1) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n) |
f (n |
1) |
|
n |
|
|
|
|
|
|
|
||||||
Без рекурсии |
|
|
|
|
|
|
|
|
|
|
|||||||
f (1) |
1 |
1 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f (2) |
1 |
2 |
2 3 |
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (3) |
1 |
2 |
3 |
3 4 |
|
6 |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f (4) |
1 |
2 |
3 |
4 |
4 5 |
|
10 |
||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (n) |
1 |
2 |
3 ... |
n |
|
n(n 1) |
|||||||||||
|
|
||||||||||||||||
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8
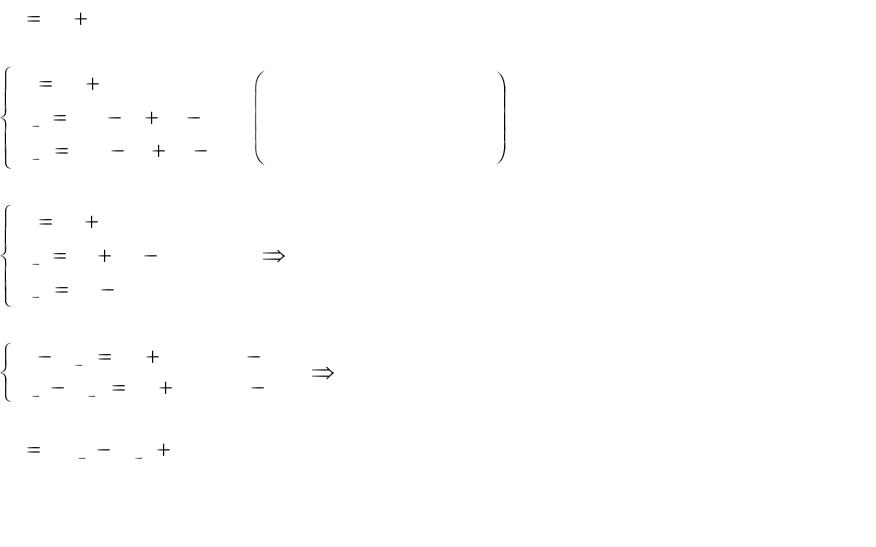
Преобразование к рекуррентному виду
Без рекурсии |
|
|
|
|
|
|
|
|
|
|
|||||||
x |
n |
|
|
4n |
n2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С рекурсией |
|
|
|
|
|
|
|
|
|
|
|||||||
|
xn |
|
|
4n |
|
n2 |
|
|
|
число |
уравнений |
|
|
|
|||
|
x |
n |
1 |
|
4(n |
1) |
(n |
1)2 |
по числу неизвестны х |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
n |
2 |
4(n 2) (n 2)2 |
x |
, n, n2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||
Решаем методом последоват ельного исключения |
Гаусса |
|
|
||||||||||||||
|
x |
n |
|
|
n2 |
4n |
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
1 |
|
n2 |
2n |
3 |
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
n |
2 |
n2 |
4 |
|
|
(3) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
xn |
|
|
xn |
2 |
4n |
4 |
|
(1) |
(3) |
Проверка |
|
|
||||
|
xn |
1 xn 2 |
2n |
1 |
(2) |
(3) |
|
|
|
|
|
||||||
|
|
n |
xn=4n+n |
2 |
xn=2xn-1-xn-2+2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
xn |
|
|
2xn |
|
xn 2 |
2 |
|
|
|
|
1 |
5 |
|
---- |
|||
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
12 |
|
---- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
21 |
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
32 |
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9

Фракталы
Определение. Фрактал – математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения (любая часть фрактала подобна всему множеству целиком). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев.
10
