32 Определение проективного преобразования.

Опр.3.1.1. Пусть (; ¯ и (; ¯ – две проективные плоскости, R – проективный репер в (; ¯, R  – в (; ¯. Проективным отображением (; ¯ на (; ¯ назы-вается отображение, действующее по правилу: точка M(; ¯ c координатами (x₁, x₂, x₃) в репере R переходит в точку M (; ¯ с теми же координатами в репере R .

Отсюда, в частности, вытекает, что A₁ переходит в A₁ , A₂ – в A₂ , A₃ – в A₃ , E – в E, т.е R переходит в R .

Можно показать, что проективным отображением будет перспективное отображение (; ¯ на (; ¯, которое возникает при центральном проецировании (; ¯ на (; ¯, а также любая композиция перспективных отображений плоскости на плоскость.

Опр.3.1.2. Проективным преобразованием плоскости (; ¯ называется проективное отображение (; ¯ на себя. Оно задается двумя реперами R и R  в плоскости (; ¯ .

Движение, подобие и аффинное преобразование плоскости (; ¯ являются частными случаями проективных преобразований.

3.2. Формулы проективного преобразования.

Пусть f : (; ¯  (; ¯ – проективное преобразование, которое задается двумя реперами R и R  , а С – матрица перехода от первого репера ко второму. Пусть M  = f(M). Найдем связь между координатами M и M  в одном репере, например, в R . Пусть M(x₁, x₂, x₃)_R , тогда M  имеет такие же координаты, только относительно R  . Пусть M (x₁, x₂ , x₃ )_R . Мы видим, что задача сводится к нахождению связи между координатами одной и той же точки M  в разных реперах R и R  , а эта связь задается формулами (2.6.1). Значит,

 x_i = (;\s\do10(k =1c_ik x_k , i = 1, 2, 3. (3.2.1)

Еще раз подчеркнем, что здесь x_k – это координаты точки до преобразования, а x_i – координаты образа этой точки.

Замечание. Проективное преобразование точек прямой определяется аналогично, т.е. с помощью двух реперов R = {A₁, A₂, E}, R = {A₁ , A₂ , E} на этой прямой и состоит в том, что точка M(x₁: x₂)_R переходит в M ( x₁: x₂)_R . Формулы преобразования имеют вид (3.2.1), где i, k = 1, 2.

Формулы проективных преобразований записываются в матричном виде: X= CX. И каждому проективному преобразованию соответствует своя невырожденная матрица C.

33 Основное свойство проективных преобразований.

Теор3.3.1.При проективном преобразовании плоск-и прям переходит в прямую.

Пусть преобразование задано реперами R и R  , а прямая a; ¯ имеет уравнение относительно R : u₁x₁+ u₂x₂ + u₃x₃ = 0. Образ этой прямой будет удовлетворять такому же уравнению относительно R  , а значит, это тоже будет прямая.

Опр. 3.4.1. Гомологией называется нетождественное проективное преобразование плоскости, имеющее точечно неподвижную (инвариант-ную) прямую, называемую осью гомологии.

Свойства гомологии.

1. Прямая, проходящая через две несовпадающие соответственные точки,

преобразуется в себя (является неподвижной).

2. Прямые, проходящие через несовпадающие соответственные точки (не

принадлежащие одной прямой), проходят через одну неподвижную

(инвариантную) точку, называемую центром гомологии.

3. Прямая, не проходящая через центр гомологии, и ее образ Перес-ся

на оси гомологии.

Опр. 3.4.1. Гомология, центр которой не принадлежит оси, наз. гиперболической. Гомология, центр которой принадлежит оси, наз. параболической.

Гомология задается осью s, центром S и парой соответственных точек, лежащих на прям, проходящей через центр. Обозн.такую гомологию(S, s; A, A).

Соответственные при гомологии фигуры называются гомологичными. Примерами таких фигур являются трехвершинники из теоремы Дезарга. Фактически, теоремой Дезарга доказывается существование гомологии. Pисунок, 2.1, сопровождающий эту теорему, демонстрирует пример построения соответственных точек при гомологии (S, s; A, A), когда S – собственная точка.

Построение соответственных точек (фигур).

Пусть (S, s; A, A) – гомология, M – произвольная не двойная точка.

Найдем ее образ M= (M). Для этого последовательно проводим прямые 1) SM; 2) AM, AM  s = P (=P); 3) PA  M= AM  PA.

Н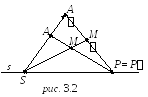а рис. 3.1 – гиперболическая, на рис. 3.2  – параболическая.

На расширенной плоскости выделяются частные виды гомологии.

1. Перспективно-аффиное (родственное) преобразование. Это гомология с несобственным центром. Среди них имеются а) отражения со сжатием (или растяжением) к оси; б) отражения – осевые симметрии (косая симметрия, симметрия); в) сжатия к оси (либо растяжения); г) параллельные переносы – ( S_ , s_ , A, A); д) сдвиги (перекосы) – ( S_ , s, (S_ s), A, A).2. Гомотетия – ( S, s_ , A, A); в частности это может быть центральная симметрия